Заземление плоских пластин
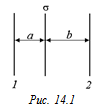Задача 14.1. Две бесконечные плоские проводящие пластины находятся на расстоянии а и b по обе стороны от третьей (рис. 14.1). Средняя пластина заряжена с поверхностной плотностью заряда s > 0, а крайние – не заряжены. Найти поверхностную плотность заряда на крайних пластинах после того, как обе они будут заземлены. Нарисовать картину силовых линий до и после заземления.
| s а b | Решение. После заземления крайние пластины приобретут отрицательный заряд, а их потенциалы будут равны нулю. Равенство нулю потенциалов будет означать, что электрического поля слева от пластины 1 и справа от пластины 2 не будет, так как работа по перемещению единичного положительного заряда с каждой из этих пластин на бесконечность теперь равна нулю. |
| s1 = ? s2 = ? | |
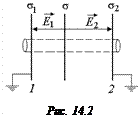Применим теорему Гаусса: мысленно возьмем цилиндр (рис. 14.2) и рассчитаем поток через него:
,
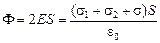так как Е = 0, то
s1 + s2 + s = 0. (1)
Пусть потенциал средней пластины равен j0, тогда работа по перемещению пробного заряда q со средней пластины на пластины 1 и 2 будет одинакова и равна
А = q(j0 – 0) = q E1a = qE2b.
Отсюда
Е1а = Е2b. (2)
Заметим, что из равенства (2) следует, что чем меньше промежуток между пластинами, тем больше там напряженность поля.
Вычислим значения Е1 и Е2 как суперпозиции полей зарядов всех трех пластин:
, 
.
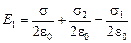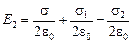Подставляя эти значения в (2), получим
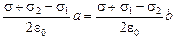Þ
(s + s2 – s1)а = (s + s1 – s2)b.
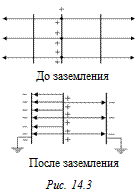Мы получили систему двух уравнений с двумя неизвестными s1 и s2:
Решив ее, получим
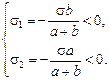
Картины силовых линий показаны на рис. 14.3.
СТОП! Решите самостоятельно: В6, С3, С5, С8.
Плотность энергии
Дата добавления: 2016-04-11; просмотров: 1168;