Задачи очень трудные. D1. Бесконечный заряженный цилиндр радиуса r имеет объемную плотность заряда r и окружен соосной с ним заземленной цилиндрической металлической поверхностью
D1. Бесконечный заряженный цилиндр радиуса r имеет объемную плотность заряда r и окружен соосной с ним заземленной цилиндрической металлической поверхностью радиуса R. Найдите зависимость потенциала поля этой системы от расстояния до оси цилиндра.
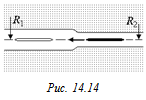 D2. Вдоль оси длинного цилиндрического канала, вырезанного в проводнике, пролетает тонкий стержень, линейная плотность заряда которого r (рис. 14.14). Длина стержня l много больше радиусов R1и R2. Вдали от области сужения канала справа скорость стержня υ0. Найдите скорость стержня вдали от области сужения канала слева. Масса стержня т.
D2. Вдоль оси длинного цилиндрического канала, вырезанного в проводнике, пролетает тонкий стержень, линейная плотность заряда которого r (рис. 14.14). Длина стержня l много больше радиусов R1и R2. Вдали от области сужения канала справа скорость стержня υ0. Найдите скорость стержня вдали от области сужения канала слева. Масса стержня т.
D3.Внутренний радиус металлической сферической оболочки равен а, ее внешний радиус равен b, а центр находится в начале координат. В оболочке просверлено небольшое отверстие. Полный заряд оболочки равен нулю. Какую работу нужно затратить, чтобы заряд q1перевести из бесконечности через отверстие в начало координат? Чему равна эта работа, если полный заряд оболочки равен q2?
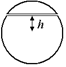 D4. Разрезанный заряженный шар. Заряженный металлический шар радиуса R разрезан на две части плоскостью, проходящей на расстоянии h от центра шара (рис. 14.15). С какой силой отталкиваются друг от друга эти части? Полный заряд шара равен Q.
D4. Разрезанный заряженный шар. Заряженный металлический шар радиуса R разрезан на две части плоскостью, проходящей на расстоянии h от центра шара (рис. 14.15). С какой силой отталкиваются друг от друга эти части? Полный заряд шара равен Q.
Рис. 14.15
Закон сохранения энергии
Для электростатики
Потенциальной энергией точечного заряда в данной точке электростатического поля называется величина, равная работе сил поля по перемещению точечного заряда из данной точки в точку, значение потенциальной энергии в которой принято равным нулю.
Заметим, что, например, для поля, созданного равномерно заряженной сферой или точечным зарядом, потенциальная энергия берется равной 0 на бесконечности, а для поля, созданного бесконечной равномерно заряженной плоскостью – на некоторой произвольной плоскости, параллельной плоскости, создающей поле (или на ней самой).
Если в некоторой точке электростатического поля значение потенциала равно j, то значение потенциальной энергии точечного заряда q, находящегося в этой точке, равно
П = qj.
Если при перемещении точечного заряда из некоторой точки 1 в точку 2 в электростатическом поле никакие другие силы, кроме сил поля, на заряд не действуют, то полная механическая энергия заряда в этом поле, определяемая как сумма его кинетической и потенциальной энергии, сохраняется:
П1 + К1 = П2 + К2 = const.
Учитывая, что П = qj, а К = тυ2/2 (где q – заряд, а т – масса точечного заряда),можно эту формулу записать в виде
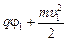 =
= 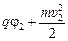 . (15.1)
. (15.1)
Теорема о кинетической энергии.Изменение кинетической энергии тела равно работе равнодействующей силы: DК = А.
Доказательство. Пусть тело массой т под действием силы 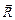 на расстоянии S изменило свою скорость с υ1 до υ2 (ограничимся случаем, когда
на расстоянии S изменило свою скорость с υ1 до υ2 (ограничимся случаем, когда 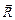 сонаправлена с перемещением тела). Тогда
сонаправлена с перемещением тела). Тогда
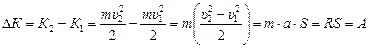 ,
,
что и требовалось доказать.
Докажем формулу (15.1). Пусть заряд q под действием сил только электростатического поля переместится из точки 1 с потенциалом j1 в точку 2 с потенциалом j2, изменив свою скорость с υ1 до υ2. По теореме о кинетической энергии
DК = Аполя Þ DК = К2 – К1 = 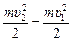 .
.
С другой стороны, Аполя = q(j1 – j2), тогда
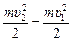 = q(j1 – j2), (15.2)
= q(j1 – j2), (15.2)
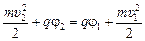 .
.
Формула (15.1) доказана.
Заметим, что заряд q в формулах (15.1) и (15.2) берется с учетом знака.
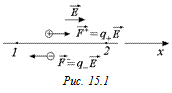 Если j1 > j2, то проекция вектора
Если j1 > j2, то проекция вектора  на ось, направляемую от точки 1 к точке 2, положительна (поле направлено в сторону убывания потенциала) (рис. 15.1). Поэтому если j1 > j2, то у положительного заряда υ2 > υ1, т.е. положительный заряд ускоряется в направлении убывания потенциала. У отрицательного заряда υ2 < υ1, т.е. при движении в направлении убывания потенциала поле тормозит отрицательный заряд.
на ось, направляемую от точки 1 к точке 2, положительна (поле направлено в сторону убывания потенциала) (рис. 15.1). Поэтому если j1 > j2, то у положительного заряда υ2 > υ1, т.е. положительный заряд ускоряется в направлении убывания потенциала. У отрицательного заряда υ2 < υ1, т.е. при движении в направлении убывания потенциала поле тормозит отрицательный заряд.
Задача 15.1. Точечный заряд переместился в электростатическом поле из точки 1 с потенциалом j1 = 200 В в точку 2 с потенциалом j2 = 100 В. Определить изменение кинетической энергии заряда в случае, если: 1) q1 = 1×10–6 Кл; 2) q1 = –1×10–6 Кл.
| j1 = 200 В j2 = 100 В q1 = 1×10–6 Кл q2 = –1×10–6 Кл | Решение. Изменение кинетической энергии равно работе поля: DК = q(j1 – j2), тогда DК1 = q1(j1 – j2) = 1×10–6 Кл×(200 В – 100 В) = = 1×104 Дж > 0; DК2 = q2(j1 – j2) = –1×10–6 Кл×(200 В – 100 В) = = –1×104 Дж < 0. |
| DК1,DК2 = ? |
Вывод: В первом случае DК1 > 0 (положительный заряд ускорился, двигаясь от большего потенциала к меньшему); во втором случае DК2 < 0 (отрицательный заряд замедлился, двигаясь от большего потенциала к меньшему).
СТОП! Решите самостоятельно: А1, А2.
Задача 15.2. Заряженная частица движется в электростатическом поле из точки 1 с потенциалом j1 = 200 В (точно) в некоторую точку 2 . Скорость частицы в точке 1 υ1 = 1,0×105 м/с, а в точке 2 υ2 = 2,0×105 м/с. Определить потенциал в точке 2, если частица с зарядом е = 1,6×10–19 Кл: а) протон (тр = 1,67×10–27 кг); б) электрон (те = 9,1×10–31 кг).
| j1 = 200 В υ1 = 1,0×105 м/с υ2 = 2,0×105 м/с е = 1,6×10–19 Кл тр = 1,67×10–27 кг те = 9,1×10–31 кг | Решение. Воспользуемся формулой (15.1):
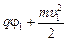 = = 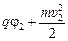 , ,
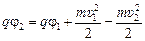 , ,
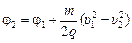 . .
|
| j2 = ? | |
1. Если частица – протон: т = тр, q = +e, тогда
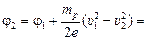
= 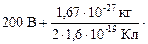 [(1,0×105 м/с)2 – (2,0×105 м/с)2 ]» 43 В.
[(1,0×105 м/с)2 – (2,0×105 м/с)2 ]» 43 В.
Заметим, что протон, разогнавшись, оказался в точке 2 с меньшим потенциалом: 43 В < 200 В.
2. Если частица – электрон: т = те, q = –e, тогда
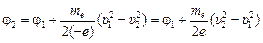 =
=
= 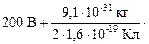 [(2,0×105 м/с)2 – (1,0×105 м/с)2] » 200,085 В.
[(2,0×105 м/с)2 – (1,0×105 м/с)2] » 200,085 В.
Электрон ускоряется в направлении увеличения потенциала.
Заметим также, что Dj = j2 – j1 = 200,085 – 200 = 0,085 В (всего!), а разогнался электрон весьма прилично: от 100 км/с до 200 км/с, но для сверхлегкого электрона эта скорость – пустяк!
Ответ: а) 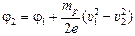 » 43 В;
» 43 В;
б) 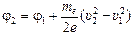 =200,17 В.
=200,17 В.
СТОП! Решите самостоятельно: А3, А5, В1, В2.
Задача 15.3. Заряженная частица движется в электростатическом поле из точки 1 с потенциалом j1 = 100 В в точку 2 с потенциалом j2 = 200 В. Скорость частицы в точке 1 υ1 = 2,0×105 м/с. Найти скорость частицы в точке 2, если частица с зарядом е = =1,6×10–19 Кл: а) протон (тр = 1,67×10–27 кг); б) электрон (те = = 9,1×10–31 кг).
| j1 = 100 В j2 = 200 В υ1 = 2,0×105 м/с е = 1,6×10–19 Кл тр = 1,67×10–27 кг те = 9,1×10–31 кг | Решение. Воспользуемся формулой (15.1):
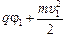 = = 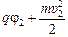 , ,
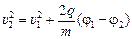 , ,
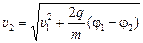 . .
|
| υ2 = ? | |
1. Если частица – протон: т = тр, q = +е. Тогда
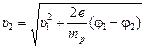 =
=
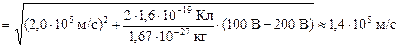 .
.
Так как 1,4×105 м/с < υ1, значит, скорость протона уменьшилась.
Читатель: А если оказалось бы, что 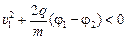 ?
?
Автор: Это означало бы, что до точки с потенциалом j2 протон просто не долетел, он остановился бы раньше!
2. Если частица – электрон: т = те, q = –е. Тогда
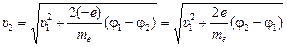 =
=
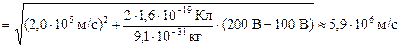 .
.
Здесь 5,9×106 м/с > υ1, значит, электрон разогнался, так как j2 > j1.
Ответ: а) 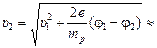 1,4×105 м/с;
1,4×105 м/с;
б) 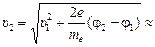 5,9×105 м/с.
5,9×105 м/с.
СТОП! Решите самостоятельно: А4, А6, В5, В6.
Дата добавления: 2016-04-11; просмотров: 1900;
