Движение точечного заряда
Во внешнем поле
Потенциальная энергия заряда
В однородном поле
Читатель: Что такое потенциальная энергия заряда в силовом поле?
Автор: Эта работа поля по перемещению заряда из данной точки в точку, которой мы припишем нулевое значение потенциальной энергии (как в случае однородного гравитационного поля).
Пусть в постоянном поле, образованном бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда s > 0, в некоторой точке С находится заряд q > 0 (рис. 16.1). Найдем его потенциальную энергию.
 Можно, например, положить П = 0 на самой плоскости. Тогда работа поля по перемещению заряда из точки C в точку 0 будет равна
Можно, например, положить П = 0 на самой плоскости. Тогда работа поля по перемещению заряда из точки C в точку 0 будет равна
 < 0.
< 0.
То есть потенциальная энергия заряда отрицательная!
Задача 16.1. Частица массой т и зарядом q > 0 движется вдоль силовых линий однородного электростатического поля напряженностью Е. Начальная скорость частицы υ0, 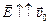 (рис. 16.2). Найти: 1) ускорение частицы; 2) скорость частицы через время t; скорость частицы на расстоянии s0 от исходной точки.
(рис. 16.2). Найти: 1) ускорение частицы; 2) скорость частицы через время t; скорость частицы на расстоянии s0 от исходной точки.
| q m E s0 υ0 t | Решение.
1. 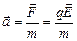 , , 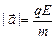 .
2. υ(t) = υ0 + at, υ(t) = υ0 + .
2. υ(t) = υ0 + at, υ(t) = υ0 + 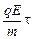 .
3. υ(s0) найдем тремя способами.
Способ 1 – кинематический. Воспользуемся формулой .
3. υ(s0) найдем тремя способами.
Способ 1 – кинематический. Воспользуемся формулой  и получим: и получим:
 , ,
| |
| а = ? υ(t) = ? υ(s0) = ? | ||
 Рис. 16.2
Рис. 16.2
| 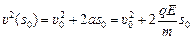 , ,
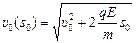 . .
| |
Способ 2.Воспользуемся теоремой о кинетической энергии: DК = А (работа всех сил). Тогда
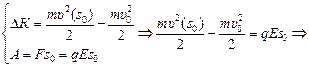
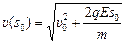 .
.
 Способ 3. Воспользуемся законом сохранения энергии: П + К = = const, где П – энергия частицы во внешнем поле. Предположим, что в начальной точке потенциал равен нулю: j(0) = 0 (рис. 16.3). Найдем j(s):
Способ 3. Воспользуемся законом сохранения энергии: П + К = = const, где П – энергия частицы во внешнем поле. Предположим, что в начальной точке потенциал равен нулю: j(0) = 0 (рис. 16.3). Найдем j(s):
Аполя = q[убыль потенциала],
qEs0 = q[j(0) – j(s)],
j(s) = –Es0.
Применим формулу (15.1):
qj1 + К1 = qj2 + К2,
q×0 + 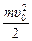 = q(–Es0) +
= q(–Es0) + 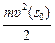 ,
,
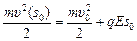 ,
,
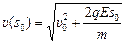 .
.
Ответ:  ; υ(t) = υ0 +
; υ(t) = υ0 + 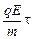 ;
; 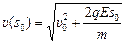 .
.
СТОП! Решите самостоятельно: А2, В3, С2.
Задача 16.2. Частица массой т и зарядом q влетает в электростатическое поле напряженностью Е в направлении, противоположном направлению вектора  , с начальной скоростью υ0
, с начальной скоростью υ0 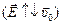 . Через какое время t0 частица остановится? Какую работу Ап совершит поле с момента начала движения до остановки частицы? На каком расстоянии s0 от исходной точки частица остановится?
. Через какое время t0 частица остановится? Какую работу Ап совершит поле с момента начала движения до остановки частицы? На каком расстоянии s0 от исходной точки частица остановится?
| т q E υ0 | Решение. Введем ось х υ0 (рис. 16.4).
Рис. 16.4 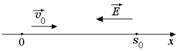 1. Найдем t0. Ускорение
1. Найдем t0. Ускорение  . Исходя из рис. 16.4 получаем . Исходя из рис. 16.4 получаем 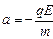 . Скорость . Скорость  . .
|
| t0= ? Аполя= ? s0 = ? | |
В момент остановки скорость равна нулю:  , тогда
, тогда
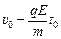 = 0,
= 0,  .
.
2. Найдем Аполя. Воспользуемся теоремой о кинетической энергии: DК = Аполя. Тогда
0 – 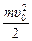 = Аполя или Аполя = –
= Аполя или Аполя = – 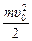 .
.
3. Найдем s0. Опять воспользуемся теоремой о кинетической энергии: DК = Аполя.
Аполя = Fs0cos180° = –qEs0,
0 – 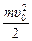 = –qEs0,
= –qEs0, 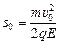 .
.
Ответ:  ; Аполя = –
; Аполя = – 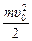 ;
; 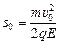 .
.
СТОП! Решите самостоятельно: А1, В1, В4.
Задача 16.3. Частица массы т и зарядом q > 0 влетает с горизонтальной скоростью υ0 в однородное электростатическое поле напряженностью Е, как показано на рис. 16.5. Считая, что начальные координаты частицы в системе х, у равны (0, 0), найти υх(t), υу(t), υ(t), х(t), у(t).
| т q υ0 Е | 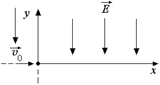 Рис. 16.5
Решение. Задача полностью аналогична задаче о теле, брошенном горизонтально вблизи поверхности Земли[1]. Поэтому приведем лишь краткие выкладки: Рис. 16.5
Решение. Задача полностью аналогична задаче о теле, брошенном горизонтально вблизи поверхности Земли[1]. Поэтому приведем лишь краткие выкладки:
|
| υх(t) = ? υу(t) = ? υ(t) = ? х(t) = ? у(t) = ? |
 ;
; 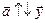 ;
; 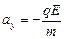 , ах = 0;
, ах = 0;
υ0у = 0, υ0х = υ0;
υх(t) = υ0х + ахt = υ0 + 0×t = υ0 = const;
υу(t) = υ0у + ауt =  ;
;
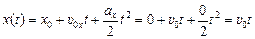 ;
;
 ;
;
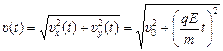 .
.
Ответ: υх(t) = υ0; υу(t) = 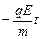 ;
; 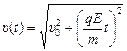 ;
;
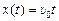 ;
;  .
.
СТОП! Решите самостоятельно: С4–С6.
Задача 16.4. Частица массы т и зарядом q влетает в электростатическое поле напряженностью Е, как показано на рис. 16.6. Вектор начальной скорости 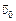 составляет угол a с осью х,
составляет угол a с осью х, 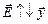 . Найти ах, ау, υх(t), υу(t), х(t), у(t), максимальную координату уmax, координату хв точки вылета частицы из поля.
. Найти ах, ау, υх(t), υу(t), х(t), у(t), максимальную координату уmax, координату хв точки вылета частицы из поля.
| т q Е υ0 a | Рис. 16.6  Решение. Задача полностью аналогична задаче о теле, брошенном под углом к горизонту[2], только вместо силы
Решение. Задача полностью аналогична задаче о теле, брошенном под углом к горизонту[2], только вместо силы  здесь участвует сила здесь участвует сила 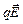 . Поэтому приведем лишь краткие выкладки решения: . Поэтому приведем лишь краткие выкладки решения:
|
| ах, ау = ? υх(t), υу(t) = ? х(t), у(t) = ? уmax = ? хв = ? | |
 , ах = 0,
, ах = 0, 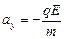 ;
;
υ0х = υ0cosa, υх(t)= υ0cosa = const;
υ0у= υ0sina, υy(t)= υ0sina 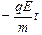 ;
;
 ;
;
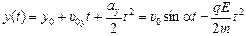 .
.
Найдем уmax с помощью теоремы о кинетической энергии:
DК = Аполя;
DК = К(уmax) – К0 = 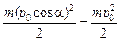 ,
,
Аполя = –qEymax;
 = –qEymax;
= –qEymax;
qEymax = 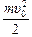 (1 – cos2a), ymax =
(1 – cos2a), ymax = 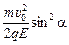 .
.
Чтобы найти хв (т.е. координату х в момент времени tв), сначала определим момент вылета tв:
y(tв) = 0,
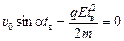 Þ
Þ  .
.
Отсюда
хв = х(tв) = 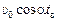 =
=  =
=
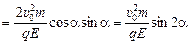 .
.
Ответ: ах = 0; 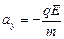 ; υх(t)= υ0cosa; υy(t)=
; υх(t)= υ0cosa; υy(t)=  ;
;  ;
; 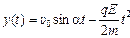 ; ymax =
; ymax =  ; хв =
; хв = 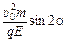 .
.
СТОП! Решите самостоятельно: С7, С8.
Задача 16.5. Маленький шарик зарядом q > 0 и массы т подвешен на нити длиной l в однородном вертикальном электростатическом поле Е, направленном вертикально вниз. В начальный момент шарик отклонен на угол a от вертикали (рис. 16.7). Найти: а) скорость шарика при его перемещении в положение равновесия; б) работу поля при перемещении шарика в положение равновесия; в) силу натяжения нити при прохождении положения равновесия. Силой тяжести пренебречь.
| Е m l q > 0 a | Решение. Как видно из рисунка, в вертикальном направлении шарик сместится на Dу = =l(1 – cosa). Поскольку работа однородного поля не зависит от траектории, то Аполя = qEDу = qEl(1 – cosa). | 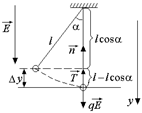 Рис. 16.7
Рис. 16.7
|
| υ = ? Аполя = ? Т = ? |
Согласно теореме о кинетической энергии
DК = Аполя Þ  – 0 = qEl(1 – cosa),
– 0 = qEl(1 – cosa),
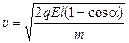 .
.
Запишем второй закон Ньютона в проекции на направление нормали 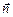 :
: 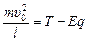 . Отсюда
. Отсюда
 .
.
Ответ: Аполя = qEl(1 – cosa); 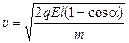 ;
;
Т = 
СТОП! Решите самостоятельно: С9, С10.
Задача 16.6. К неподвижному заряженному шару радиуса R и зарядом Q > 0 из бесконечности движется положительно заряженная частица массой т и зарядом q > 0 с начальной скоростью υ0, направленной к центру шара (рис. 16.8). Определить: а) скорость частицы на расстоянии r1 от центра шара; б) минимальное расстояние rmin, которое сможет пролететь частица до центра шара; в) минимальную скорость υ0min, которой должен обладать заряд q на бесконечности, чтобы долететь до поверхности шара.
| т R Q q υ0 r1 |  Рис. 16.8
Решение. а) Воспользуемся законом сохранения энергии qj + К = const: Рис. 16.8
Решение. а) Воспользуемся законом сохранения энергии qj + К = const:
 , ,
|
| υ1 = ? rmin = ? υ0min = ? |
 Þ
Þ  .
.
б) Применим этот же закон для случая остановки частицы на расстоянии rmin от центра шара:
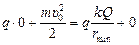 Þ
Þ  Þ 2kqQ =
Þ 2kqQ = 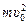 rmin Þ
rmin Þ
rmin = 2  .
.
в) Применим этот же закон для случая остановки частицы на расстоянии R от центра шара:
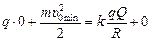 Þ
Þ 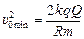 Þ
Þ
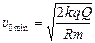 .
.
Ответ:  ; rmin = 2
; rmin = 2  ;
; 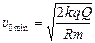 .
.
СТОП! Решите самостоятельно: А3, В5, В7, С12.
Задача 16.7. До какого максимального заряда можно зарядить металлический шар радиуса R = 0,10 м, если облучать его электронами, имеющими на бесконечности скорость υ0 = 1,0×106 м/с (рис. 16.9)? Масса электрона те = 9,1×10–31 кг, заряд е = 1,6×10–19 Кл.
| R = 0,10 м υ0 = 1,0×106 м/с те = 9,1×10–31 кг е = 1,6×10–19 Кл | Рис. 16.9  Решение. Зарядка шара кончится тогда, когда
Решение. Зарядка шара кончится тогда, когда
|
| Q = ? | |
электрон подлетит к шару с нулевой скоростью. Воспользуемся законом сохранения энергии: еj + К = const, тогда
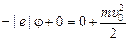 ;
; 
(мы учли, что е < 0 и заряд шара Q < 0).
 Þ
Þ 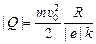 =
=
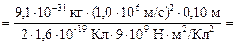 3,2×10–11 Кл.
3,2×10–11 Кл.
Ответ: 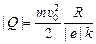 = 3,2×10–11 Кл.
= 3,2×10–11 Кл.
СТОП! Решите самостоятельно: В8, С17, С18.
Задача 16.8. Из бесконечности по направлению к двум концентрическим сферам радиусами R и 2R и одинаковыми зарядами Q с нулевой начальной скоростью движется электрон массой т и зарядом е. Пролетев через маленькое отверстие в сферах, электрон попадает в их общий центр (рис. 16.10). Найти скорость электрона в центре сфер.
| R, 2R Q e, т | Решение. В центре сфер потенциал равен
 . .
|
| υ0 = ? |
 Воспользуемся законом сохранения энергии: еj + К = const, тогда
Воспользуемся законом сохранения энергии: еj + К = const, тогда
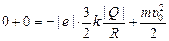 ,
,
υ0 = 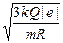 .
.
Ответ: υ0 = 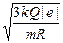 .
.
СТОП! Решите самостоятельно: В6, С13, С20.
Дата добавления: 2016-04-11; просмотров: 2252;
