ЗАЗЕМЛЕНИЕ ПРОВОДНИКОВ

СУПЕРПОЗИЦИЯ ПОЛЕЙ ЗАРЯЖЕННЫХ СФЕР.

Задача 13.1. Незаряженный проводящий шар радиуса R внесли в электрическое поле точечного заряда q (рис. 13.1). Расстояние между центром шара и зарядом равно r. Определить потенциал шара.

q r R	Решение. При внесении шара в электрическое поле на нем индуцируются заряды. Напряженность поля внутри шара равна векторной сумме напряженностей	Рис. 13.1
j = ?

полей точечного заряда q и заряда, индуцированного на шаре, и равна нулю:

,

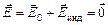где 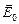– напряженность поля точечного заряда.

Поверхность шара является эквипотенциальной поверхностью. Внутри шара потенциал постоянен и равен потенциалу поверхности. Поэтому, определив потенциал в любой точке внутри шара и на его поверхности, мы решим задачу.

Определим потенциал в центре шара. Он равен сумме потенциалов поля, созданного зарядом q, и поля, созданного зарядами, индуцированными на поверхности шара:

,

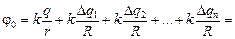
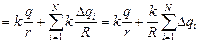где Dq_i – величина индуцированного заряда на малом элементе площади поверхности шара DS_i, R – радиус шара.

Поскольку первоначально шар не был заряжен, то 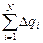= 0. Таким образом, потенциал равен потенциалу той точки поля, где находится центр шара.

Ответ: j = kq/r.

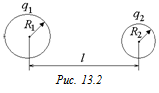Задача 13.2. Две проводящие сферы радиусами R₁ и R₂ и зарядами q₁ и q₂ находятся на расстоянии l друг от друга (рис. 13.2). Определить потенциалы каждой сферы. Перераспределением зарядов на сферах из-за индукции пренебречь.

q1 q2 R1 R2 l	Решение. Поле, созданное зарядами сферы радиуса R, при r > R точно такое же, как поле точечного заряда, расположенного в центре сферы. Потенциал первой сферы есть алгебраическая сумма потенциалов двух полей: поля «своих» зарядов и поля зарядов второй сферы: j1 = jполя зарядов сферы1 + jполя зарядов сферы2 = .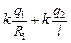
j1 = ? j2 = ?

Для второй сферы аналогично j₂ = .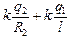

Ответ: j₁ = ; j₂ = .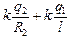

СТОП! Решите самостоятельно: В3, С7.