Расчет сопротивления участка цепи
Задача 11.5.Вычислите сопротивление участка цепи, изображенного на рис. 11.17. Значения сопротивлений проводников в омах указаны на рисунке. Все значения считать точными.
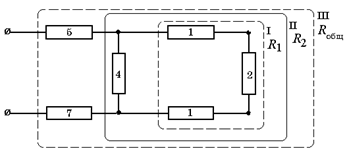
Рис. 11.17
Решение.Будем решать задачу последовательно.
1. Вычислим сопротивление участка I. Согласно формуле (11.3):
R1 = 1 Ом + 2 Ом + 1 Ом = 4 Ом.
2. Участок II представляет собой два сопротивления: 4 Ом и R1 = 4 Ом, соединенные параллельно. Согласно формуле (11.7):
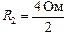 = 2 Ом.
= 2 Ом.
3. Участок III представляет собой три последовательно соединенных сопротивления: 5 Ом, R2 = 2 Ом и 7 Ом. Согласно формуле (11.3):
Rобщ = 5 Ом + 2 Ом + 7 Ом = 14 Ом.
Ответ: Rобщ = 14 Ом.
СТОП! Решите самостоятельно: А6, В19–В21, С11, С13.
Задача 11.6. Определите сопротивление R показанной на рис. 11.18 цепи, если сопротивление каждого звена R0.
| R0 | 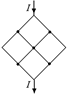 а а 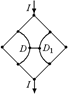 б б 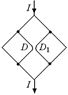 Рис. 11.18 Рис. 11.19
Рис. 11.18 Рис. 11.19
|
| R = ? | |
Решение. Непосредственно разбить данную схему на участки, состоящие только из последовательно соединенных или только из параллельно соединенных проводников не получится.
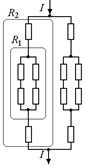 Рис. 11.20
Рис. 11.20
| Перерисуем нашу схему в виде, показанном на рис. 11.19,а. Из симметрии схемы очевидно, что потенциалы точек D и D1 равны: 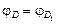 . А значит, ток по проводнику, соединяющему эти точки не течет. Но тогда этот проводник можно удалить, и мы получим схему (11.19,б). Соответствующая эквивалентная схема представлена на рис. 11.20. Сопротивления такого участка подсчитать уже легко: . А значит, ток по проводнику, соединяющему эти точки не течет. Но тогда этот проводник можно удалить, и мы получим схему (11.19,б). Соответствующая эквивалентная схема представлена на рис. 11.20. Сопротивления такого участка подсчитать уже легко:
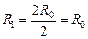 , R2 = R0 + R0 + R0 = 3R0, , R2 = R0 + R0 + R0 = 3R0,
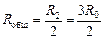 . .
|
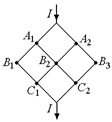 Рис. 11.21
Рис. 11.21
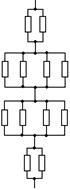 Рис. 11.22
Рис. 11.22
|
Читатель: По-моему, в данной схеме из соображений симметрии равны потенциалы точек В1, В2 и В3 (рис. 11.21)!
Автор: Да, Вы правы.
Читатель: Но тогда их можно соединить, и эквивалентная схема будет иметь вид, показанный на рис. 11.22.
Автор: Это верно! Попробуйте подсчитать сопротивление Вашей эквивалентной схемы.
Читатель: Тогда
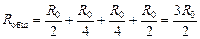 .
.
Автор: Как видите, в данном случае точки с одинаковыми потенциалами можно с одинаковым успехом как соединить, так и разъединить. Результат от этого не изменится.
Ответ: 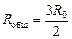 .
.
СТОП! Решите самостоятельно: В24, В25, С14, С18–С20.
Задача 11.7. Вычислить сопротивление проволочного тетраэдра, к двум вершинам которого подведено напряжение. Сопротивление каждого ребра тетраэдра – r.
| r | Решение. 1. Проведем сечение через ребро 12 и точку А, лежащую на середине ребра 34 (рис. 11.23). Отметим, что |
| R = ? | |
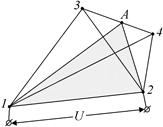 Рис. 11.23
Рис. 11.23
|
схема совершенно симметрична относительно этого сечения и, следовательно, точки 3 и 4 находятся в физически «равноправном» положении. Поэтому можно утверждать, что по ребрам 13 и 14 течет одинаковый ток, а следовательно, потенциалы точек 3 и 4 равны. В самом деле, запишем закон Ома для участков цепи 13 и 14, получим
j1 – j3 = Ir, j1 – j4 = Ir .
Отсюда j3 = j4.
2. Поскольку j3 = j4, ток через ребро 34, равен нулю:
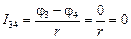
(закон Ома для участка 34).
3. Если удалить ребро 34, то токи в остальных проводниках от этого нисколько не изменятся, а значит, не изменятся и потенциалы всех узлов схемы. Поэтому схема после удаления ребра 34 останется эквивалентной исходной, а её сопротивление будет таким же, как у исходной схемы (рис. 11.24,а).
а) 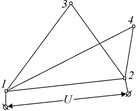 б)
б) 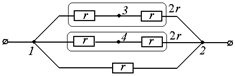
Рис. 11.24
4. Перерисуем схему на рис. 11.24,а в более привычном виде, показанном на рис. 11.24,б, и найдем её сопротивление R:
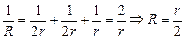 .
.
Читатель: Если потенциалы точек 3 и 4 равны, то нельзя ли их соединить в одну? Ведь токи в остальных проводниках от этого не должны измениться, а значит, такое преобразование не изменит полного сопротивления участка цепи.
Автор: Так сделать можно! Покажем, что общее сопротивление участка, рассчитанное с помощью такого преобразования схемы, будет также равно r/2 (рис. 11.25,а).
Преобразуем схему к виду, показанному на рис. 11.25,б, тогда
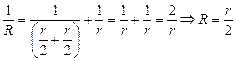 .
.
а) 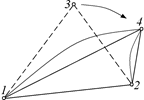 б)
б) 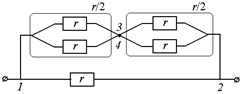
Рис. 11.25
Ответ: 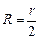 .
.
СТОП! Решите самостоятельно: В26, В27, С22–С24.
Задача 11.8. К источнику тока с напряжением U = 12,0 В присоединены две лампочки (рис. 11.26). Сопротивления участков цепи r1 = r2 = r3 = r4 = r = 1,50 Ом. Сопротивления лампочек R1 = R2 = = R = 36,0 Ом. Найти напряжение на каждой лампочке.
| U = 12,0 В r1 = r2 = r3 = r4 = r = 1,50 Ом R1 = R2 = R = 36,0 Ом | Рис. 11.26 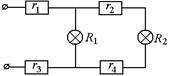
|
| U1 = ? U2 = ? | |
Решение. Сначала найдем общее сопротивление 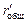 .
.
Рис. 11.27 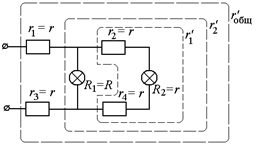
Как видно из рис. 11.27:
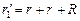 = 1,50 + 1,50 + 36,0 = 39,0 Ом;
= 1,50 + 1,50 + 36,0 = 39,0 Ом;
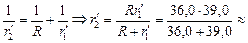 18,72 Ом;
18,72 Ом;
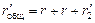 = 1,50 + 1,50 + 18,72 » 21,72 Ом.
= 1,50 + 1,50 + 18,72 » 21,72 Ом.
Вычислим силу тока I0 в неразветвленной части цепи
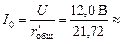 0,552 А.
0,552 А.
Пусть U1 – искомое напряжение на лампе R1, тогда справедливо
U = I0r1 + U1 + I0r3 Þ U1 = U – I0(r1 + r3) = U – I0×2r =
= 12,0 В – 0,552 А × 2 × 1,50 » 10,34 В » 10,3 В.
Рассмотрим три последовательно соединенных сопротивления: r2, R2 и r4. Их общее сопротивление 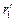 = 39,0 Ом, тогда сила тока на этом участке равна
= 39,0 Ом, тогда сила тока на этом участке равна 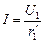 , а искомое напряжение на лампе R2
, а искомое напряжение на лампе R2
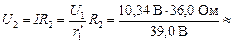 9,54 В.
9,54 В.
Ответ: U1 » 10,3 В; U2» 9,54 В.
СТОП! Решите самостоятельно: В28, С25, С26.
Задача 11.9. Если на вход электрической цепи (рис. 11.28) подано напряжение U1 = 100 В, то напряжение на выходе U3 = 40 В. При этом через резистор R2 идет ток I2 = 1 А. Если на выход цепи подать напряжение 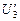 = 60 В, то напряжение на входе будет
= 60 В, то напряжение на входе будет 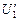 = = 15 В. Определить величины сопротивлений R1, R2, R3. Все значения точные.
= = 15 В. Определить величины сопротивлений R1, R2, R3. Все значения точные.
U1 = 100 В, U3 = 40 В
I2 = 1 А
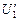 = 15 В, = 15 В, 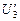 = 60 В = 60 В
| 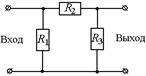 Рис. 11.28 Рис. 11.28
|
| R1 = ? R2 = ? R3 = ? | |
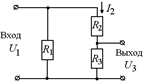 Рис. 11.29
Рис. 11.29
| Решение. В первом случае схема имеет вид, показанный на рис. 11.29. Здесь
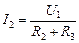 , (1)
U3 = I2R3. (2) , (1)
U3 = I2R3. (2)
|
Из (2) находим 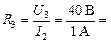 40 Ом.
40 Ом.
Из (1): 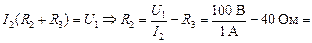 60 Ом.
60 Ом.
Во втором случае схема имеет вид, показанный на рис. 11.30. Тогда
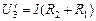 , (3) , (3)
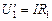 , (4)
Из (3) и (4) находим: , (4)
Из (3) и (4) находим:
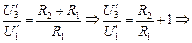
|
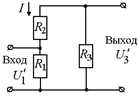 Рис. 11.30
Рис. 11.30
|
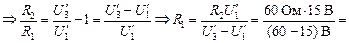 20 Ом.
20 Ом.
Ответ: R1 = 20 Ом; R2 = 60 Ом; R3 = 40 Ом.
СТОП! Решите самостоятельно: С27–С29.
Мостик без тока
Задача 11.10. В цепи на рис. 11.31 R1 = 1 Ом, R2 = 2 Ом, R3 = = 3 Ом. Найти сопротивление R4, зная, что на участке CD нет тока. Все значения точные.
Рис. 11.31 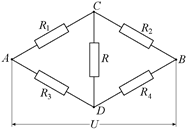
| |
| R1 = 1 Ом R2 = 2 Ом R3 = 3 Ом | |
| R4 = ? | |
Решение. Поскольку через сопротивление R ток не течет, его можно удалить, тогда схема примет вид, показанный на рис. 11.32.
Мы получили две параллельно соединенные ветви, для каждой из них запишем закон Ома:
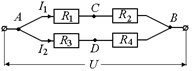 Рис. 11.32
Рис. 11.32
| 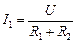 , (1) , (1)
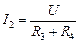 . (2) . (2)
|
Поскольку через сопротивление R ток не течет, то потенциалы точек С и D равны, а значит, равны напряжения на сопротивлениях R1 и R3:
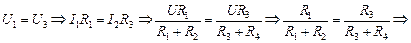
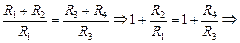
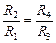 . (11.9)
. (11.9)
Из формулы (11.9) получаем:
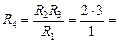 6 Ом.
6 Ом.
Ответ: 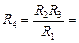 6 Ом.
6 Ом.
СТОП! Решите самостоятельно: В29, В30, С30, D4.
Мостик с током
Читатель: Если потенциалы двух точек схемыравны между собой, то следует ли из этого, что ток между этими точками не течет?
Автор:Нет! Нe следует, если между этими точками включен проводник с нулевым сопротивлением.
Рассмотрим соединительный провод 132 с нулевым сопротивлением (рис. 11.33,а): по закону Ома j1 – j2 = I × 0 Þ j1 = j2. Ток через сопротивление R1равен 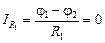 . Следовательно, весь ток, поступивший в точку 1, пойдет по соединительному проводу 132, хотя разность потенциалов между точками 1 и 2 равна нулю.
. Следовательно, весь ток, поступивший в точку 1, пойдет по соединительному проводу 132, хотя разность потенциалов между точками 1 и 2 равна нулю.
а) 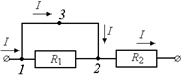 б)
б) 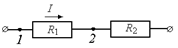
Рис. 11.33
Читатель: Если потенциалы двух точек равны, то можно ли удалить из схемы на рис. 11.33а проводник, соединяющий эти точки, не изменив при этом токи во всех остальных проводниках участка?
Автор: Вообще говоря, нет! Если в схеме на рис. 11.33,а удалить соединительный провод 132, соединяющий точки с одинаковыми потенциалами 1 и 2, то полученная схема (11.33,б) будет не эквивалентна! Ведь в этом случае через проводник R1 пойдет отличный от нуля ток и потенциалы точек 1 и 2 будут уже не равны между собой!
Проводник, включенный между двумя точками с одинаковыми потенциалами, можно смело удалять только в случае, когда его сопротивление отлично от нуля.
Если же речь идет о соединительном проводе с нулевым сопротивлением, то прежде чем его удалять, надо убедиться, что и после его удаления потенциалы тех точек, между которыми он был включен, останутся равными друг другу. В случае на рис. 11.33,а это не так.
Задача 11.11.Какой ток идет через амперметр (рис. 11.34), если R1= R4 = R,а R2 = R3 = 3R? К цепи приложено напряжение U. Сопротивление амперметра можно считать пренебрежимо малым.
| R1= R4 = R R2 = R3 = 3R U | Рис. 11.34 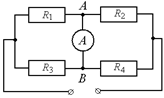
|
| I = ? | |
Решение.
Читатель: Если сопротивление амперметра практически равно нулю, то jА = jВ, следовательно, ток через амперметр не течет, и его можно удалить из схемы.
Автор: Но мы же с Вами только что выяснили, что если проводник с нулевым сопротивлением соединяет две точки с одинаковым потенциалом, то из этогововсе не следует, что через данный проводник не идет ток. Может быть, идет, а может – и нет. Надо разобраться. А удалять проводник из схемы можно только в том случае, если после удаления проводника потенциалы точек, которые он соединял, по-прежнему останутся равными друг другу. А так ли это в условии нашей задачи?
Читатель: Это было бы так, если бы выполнялось равенство 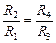 (формула (11.9)). Но в нашем случае
(формула (11.9)). Но в нашем случае 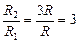 , а
, а 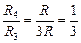 , значит, после удаления амперметра равенство jА = jВ нарушается.
, значит, после удаления амперметра равенство jА = jВ нарушается.
Автор: То есть, удалив амперметр, мы заменим нашу схему не неэквивалентную. Но вот соединить точки А и В в одну нам ничто не мешает! Тогда мы получим схему, показанную на рис. 11.35.
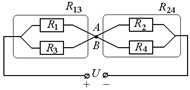 Рис. 11.35
Рис. 11.35
|
Теперь заметим, что
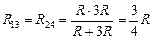 ,
,
а значит, напряжения на участках R13 и R24 равны между собой:
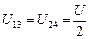 .
.
Тогда ток через сопротивление R1 равен
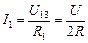 ,
,
а ток через сопротивление R2 равен
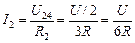 .
.
Читатель: Получается, что в точку А слева втекает ток 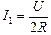 , а вытекает вправо уже
, а вытекает вправо уже 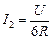 (см. рис. 11.34). Куда же девается разница I1 – I2?
(см. рис. 11.34). Куда же девается разница I1 – I2?
Автор: Разнице просто некуда больше деваться, как уйти вниз через амперметр: 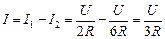 .
.
Ответ: 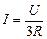 .
.
СТОП! Решите самостоятельно: В31, С31, D6.
Дата добавления: 2016-04-11; просмотров: 6401;
