Задача средней трудности

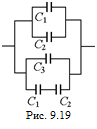В1. Найти общую емкость батареи конденсаторов, включенных по схеме рис. 9.19. Обозначения конденсаторов указаны на чертеже. Емкости конденсаторов: С₁ = 2,0 мкФ, С₂ = 3,0 мкФ, С₃ =1,0 мкФ.

В2.Параллельно одному из т = 4 последовательно соединенных одинаковых конденсаторов подключен электростатический вольтметр, емкость которого в п = 2 раза меньше емкости каждого из конденсаторов. Вольтметр показывает U = 400 В. Найти напряжение на всей батарее U₀.

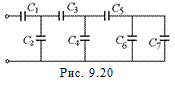
В3.Определить емкость системы, изображенной на рис. 9.20, если С₁ = С₂ = С₃ = С₄ = С₅ = С, С₆ = С₇ = = С/2.

В4.Батарея из четырех одинаковых конденсаторов включена один раз по схеме на рис. 9.21,а, другой раз – по схеме на рис. 9.21,б. В каком случае емкость батареи будет больше?

Рис. 9.21

В5. В схемах, изображенных на рис. 9.22, емкость батареи конденсаторов не изменяется при замыкании ключа K. Определите емкость конденса­тора С_х.

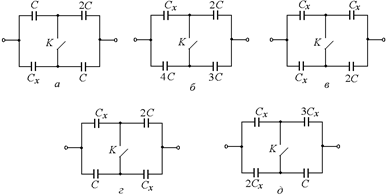
Рис. 9.22

В6.Определите емкость системы конденса­торов, изображенной на рис. 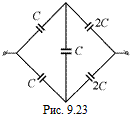9.23.

В7. Конденсатор образован 21 латунным листом, между которыми помещены стеклянные прокладки толщиной 2,0 мм. Площади латунных листов и стеклянных прокладок одинаковы и равны каждая 200 см². Листы соединены так, что образуют батарею параллельно соединенных конденсаторов. Определить ее электроем­кость, если относительная диэлектрическая проницаемость стекла равна 7,0.

Задачи трудные

С1. К конденсатору 1 емкости С, заряженному до разности потенциалов U, подсоединяется батарея из конденсаторов такой же емкости, как показано на рис. 9.24. Найти заряд на каждом из шести конденсаторов.

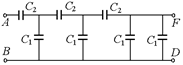
Рис. 9.24 Рис. 9.25

С2. Конденсаторы емкости С₁ = 5 мкФ и С₂ = 10 мкФ включены в схему, как показано на рис. 9.25. К точкам А и В приложена разность потенциалов U_АВ = 16 В. Найти разность потенциалов U_DF.

С3. Вычислить полную емкость С системы конденсаторов, изображенной на рис. 9.26 (С₁ = 2,0 мкФ, С₂= 4,0 мкФ).

Рис. 9.26 Рис. 9.27

С4.Конденсаторы соединили так, как указано на рис. 9.27. Чему равна емкость всей батареи, если ем­кость каждого конденсатора равна С?

С5. Батарея конденсаторов, изображенная на рис. 9.28, составлена из конденсаторов одинаковой емкости. Во сколько раз изменится общая емкость батареи, если зам­кнуть ключи K₁и K₂?

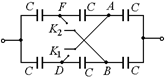
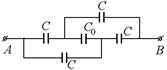
Рис. 9.28 Рис. 9.29

С6.Найти емкость системы конденсаторов, включенных между точками А и В, как показано на рис. 9.29.

С7.Двенадцать одина­ковых конденсаторов с ем­костью С каждый собраны в батарею в виде восьмигранника ACDEFB (рис. 9.30). Какова емкость этой бата­реи конденсаторов между точками А и В? С8.Из проволоки сделан куб, в каждое ребро которого включено по одному конден­сатору емкости С (рис. 9.31). Найти емкость получившейся батареи конденсаторов, если эта батарея включается в цепь проводниками, присоединенными к противоположным вер­шинам А и В куба. С9.Плоский конденсатор состоит из двух металлических пластин, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью e = 2. Как изменится емкость конденсатора, если его поместить в изолированную металлическую коробку? Просвет между стенками коробки и пластинами вдвое меньше, чем расстояние между пластинами. С10. Четыре одинаковые метал­лические пластины расположены в воздухе на равных расстояниях d друг от друга (d мало по сравне­нию с размером пластин). Площадь каждой из пластин равна S. Пла­стина 1 соединена проводником с пластинкой 3, а от пластин 2 и 4 сделаны выводы (рис. 9.32). Опре­делить емкость такого сложного конденсатора.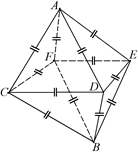

Рис. 9.30 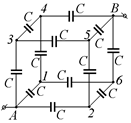  Рис. 9.31 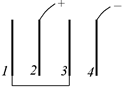  Рис. 9.32

С11. Конденсатор сделан из двух наборов пластин, как показано на рис. 9.33. Найти емкость конденсатора, пренеб­регая краевыми эффектами. Площадь каждой пластины равна S. Расстояние между пластинами одинаково и равно d (d много меньше поперечных размеров пластин). Полное число пластин равно 2п.

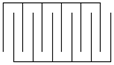Рис. 9.33 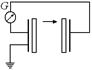Рис. 9.34

С12.Обкладки конденсатора соединены друг с другом и заземле­ны (рис. 9.34). Между обкладками помещена пластинка с зарядом q. B какую сторону потечет ток через гальванометр, если пластинку перемещать так, как показано на рисунке?

С13. Оцените, какую работу нужно совершить, чтобы из системы двух параллельных заземленных пластин (рис. 9.35) вытянуть наполовину находящуюся между ними проводящую пластину? Заряд вытягиваемой пластины Q, расстояние между ней и крайними пластинами а и b. Площадь каждой пластины S.

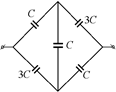Рис. 9.35 Рис. 9.36

С14. Вычислить емкость батареи конденсаторов (рис. 9.36).