Одна диэлектрическая пластина

Задача 8.5. В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d₀ вставляют пластину из диэлектрика с диэлектрической проницаемостью e и толщиной d (рис. 8.9). Определить емкость конденсатора с пластиной.

S d0 d e		Решение. Читатель: Но это же частный случай только что решенной задачи! Все то же самое, только e1 = e, e2 = 1. Сразу можно дать ответ: 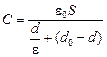. (8.2) Автор: Верно! А изменится ли ответ, если вставляемая пластинка не будет прилегать к одной из обкладок (рис. 8.10)? Читатель: Я думаю, это надо проверить. Представим конденсатор в виде трех последовательно соединенных конденсаторов с емкостями , , . 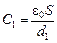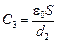Тогда
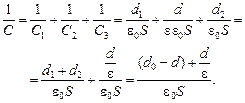
С = ?
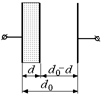Рис. 8.9
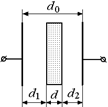Рис. 8.10

Отсюда ответ: .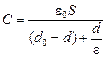

Как видим, формула ничем не отличается от (8.2)!

Автор: Значит, делаем вывод: если вставить в конденсатор диэлектрическую пластину параллельно обкладкам, то емкость получившегося конденсатора не будет зависеть от величины воздушных промежутков между пластиной и обкладками конденсатора. А величину емкости можно вычислить по формуле (8.2).

СТОП! Решите самостоятельно: А6, В10, В11, С6, D1.

Задача 8.6. В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d₀ вставляют пластину из диэлектрика с диэлектрической проницаемостью e (рис. 8.11). Определить емкость конденсатора.

S d0 e	Решение. Систему можно рассматривать как два параллельно соединенных конденсатора с емкостями 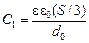, 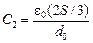.	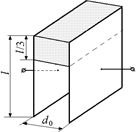Рис. 8.11
С = ?
Тогда = .

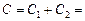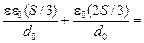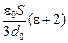Ответ: С .

СТОП! Решите самостоятельно: А7, В12–В16.

Автор: Как Вы думаете, если конденсатор на рис. 8.11 заряжен до заряда Q и изолирован, то где напряженность поля больше: в пространстве, где находится диэлектрик, или в воздушном промежутке?

Читатель: Конечно в воздушном промежутке! Ведь диэлектрик ослабляет поле в e раз. Поэтому Е^диэл = Е^возд­/e!

Автор: Да. Но, с другой стороны, обе обкладки конденсатора – эквипотенциальные поверхности, следовательно, если перенести единичный положительный заряд с одной пластины на другую, то поле совершит одинаковую работу независимо от того, в каком именно месте переносится заряд: там, где находится диэлектрик, или там, где воздушный промежуток: U = Е^диэлd = Е^воздd. А отсюда следует, что Е^диэл = Е^возд­.

Читатель: Странно…

Авто: Вспомним, что напряженность поля в конденсаторе равна 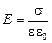, где s – поверхностная плотность заряда. Если Е^диэл = = Е^возд­, значит,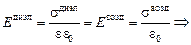 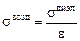. То есть заряд по обкладке распределен неравномерно: s больше в той области, где находится диэлектрик!

СТОП! Решите самостоятельно: С11.

Задача 8.7. В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d₀ вставляют пластину из диэлектрика с диэлектрической проницаемостью e (рис. 8.12). Определить емкость конденсатора.

S d0 e	Решение. Данную систему можно представить в виде трех конденсаторов, соединенных так, как показано на рис. 8.13. Тогда , ,
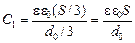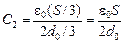С = ?
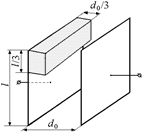Рис. 8.12 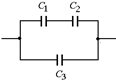  Рис. 8.13	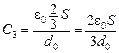. Находим общую емкость С12 конденсаторов С1 и С2 : 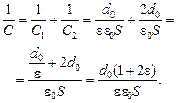Отсюда 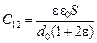. А общая емкость всей системы

С = С₁₂ + С₃ = .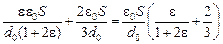

Ответ: С = .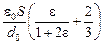

СТОП! Решите самостоятельно: В18, С12, С15.