Две диэлектрические пластины
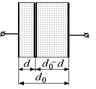 Рис. 8.8
Рис. 8.8
|
Задача 8.4. В плоский конденсатор с площадью обкладок S и расстоянием d0 между ними вставили две диэлектрические пластины, разделенные тонкой металлической пластиной (рис. 8.8). Диэлектрическая проницаемость пластин e1 и e2, толщина слоя первого диэлектрика d. Определить емкость получившегося конденсатора.
| S d0 d e1 e2 | Решение. Данную систему можно рассматривать как два последовательно соединенных конденсатора с емкостями 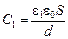 и и  . Тогда . Тогда
 . .
|
| C = ? | |
Отсюда получаем ответ: С = 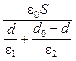 .
.
Читатель: А изменится ли емкость, если металлическую пластину убрать?
Автор: Пусть обкладки конденсатора имеют заряды +Q и –Q и конденсатор изолирован. В отсутствие диэлектриков напряженность поля была бы равна 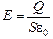 . Диэлектрики ослабляют это поле: первый в e1 раз, а второй – в e2 раз: Е1 = Е0/e1, Е2 = Е0/e2. Емкость конденсатора С = Q/U, а
. Диэлектрики ослабляют это поле: первый в e1 раз, а второй – в e2 раз: Е1 = Е0/e1, Е2 = Е0/e2. Емкость конденсатора С = Q/U, а
 .
.
Если мы уберем пластину, то величина Q не изменится, значит, не изменится и величина U, а значит, не изменится величина С = = Q/U. Отсюда следует важный практический вывод: конденсатор, заполненный несколькими параллельными слоями диэлектриков, можно рассматривать как систему последовательно соединенных конденсаторов.
СТОП! Решите самостоятельно: В8, В9, С7, С10.
Дата добавления: 2016-04-11; просмотров: 1765;
