Задачи средней трудности. В1. В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена парал­лельно обкладкам проводящая пластинка

В1. В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена парал­лельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а ее толщина намного меньше d. Найти емкость конденсатора с проводящей пластинкой, если пластинка расположена на расстоянии l от одной из обкладок конденсатора.

B2. К пластинам плоского конденсатора, одна из которых заземлена, приложено напряжение U = 100 В. В воздушный зазор шириной d = 4,0 см между пластинами вдвигается неза­ряженная тонкая металлическая пластина на расстоянии l = 3,0 см от заземленной пластины. Определить потенциал внутренней пластины и напряженность поля по обе стороны от нее. Изме­нится ли емкость конденсатора?

В3. В конденсатор, описанный в задаче В2, вдвигаются две нейтральные тонкие проводящие пластины, соединенные проводником. Пластины устанавливаются параллельно электро­дам конденсатора на расстоянии 1,0 см от каждого из них. Определить потенциалы внутренних пластин и напряженность поля. Изменится ли заряд конденсатора после введения пластин?

В4. Плоский воздушный конденсатор заряжен до раз­ности потенциалов V₀ = 50 В и отключен от источника тока. После этого в конденсатор параллельно обкладкам вносится проводящая пластинка толщины d_n = =1,0 мм. Рас­стояние между обкладками d = 5,0 мм, площади обкладок и пластинки одинаковы. Найти разность потенциалов V между обкладками конденсатора с проводящей пластинкой.

В5. На расстоянии 2,50 мм друг от друга в воздухе расположены вер 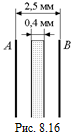тикально две параллель­ные пластины А и В (рис. 8.16), потенциалы ко­торых соответственно равны 50,0 и –50,0 В. Опре­делить напряженность образовавшегося однород­ного поля и разность потенциалов между пласти­нами, если посредине между ними помещен метал­лический лист толщиной 0,40 мм. Какую работу совершит поле при перенесении заряда 0,10×10^–2 Кл между пластиной А и про­межуточным листом?

В6. Плоский конденсатор с площадью пластин S = 10 см² и расстоянием между пластинами d = 0,2 см подключен к источнику постоянного напряжения U = 2 B (рис. 8.17). В пространство между пластинами конденсатора вводят плоскую металлическую пластину толщиной d₁ = 0,1 см. Определить заряд, прошедший через соединительные провода при введении пластины.

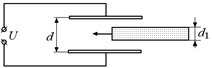
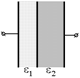
Рис. 8.17 Рис. 8.18

В7. В плоский воздушный конденсатор вставляется металлическая пла­стина толщиной d₀. Заряд на обкладках конденсатора q. Конденсатор отключен от источника. Расстояние между пластинами d, площадь пластин S. Определите изменение емкости конденсатора и энергии его электрического поля.

В8. Конденсатор имеет два диэлектрика с диэлектриче­скими проницаемостями e₁ и e₂ (рис. 8.18). При каком соотношении между толщинами d₁ и d₂ слоев диэлектриков падение потен­циала в каждом слое диэлектрика окажется равным половине разности потенциалов, приложенной к конденсатору? Найти емкость этого конденсатора, если площадь каждой пластины S.

В9. Пространство между обкладками плоского кон­денсатора заполнено тремя диэлектрическими пластинами рав­ной толщины d = 2,0 мм из стекла (e₁ = 7,0), смолы (e₂ = 6,0) и парафи­на (e₃ = 2,0). Площади обкладок конденсатора и пластин одинако­вы и равны S = 200 см². Найти емкость С такого конденсатора.

В10. Плоский конденсатор имеет площадь пластин S = 2000 см², расстояние между ними 0,5 мм. В конден­саторе находится пластинка слюды (e = 7) толщиной d₁ = 0,3 мм, в остальной части — воздух. Определить ем­кость С конденсатора.

В11. Плоский воздушный конденсатор заряжен до разности потенциалов U = 60 В и отключен от источника электриче­ского тока. После этого внутрь конденсатора параллельно обкладкам вводится пластинка из диэлектрика с диэлектри­ческой проницаемостью e = 2,0. Толщина пластинки в два раза меньше величины зазора между обкладками конденсатора. Чему равна разность потенциалов между обкладками конден­сатора после введения диэлектрика?

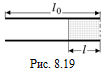
В12. Определить электроемкость конденсатора, в котором часть пространства между пластинами заполнена диэлектриком (рис. 8.19).

В13. Пространство между обкладками плоского конденсатора заполнено наполовину диэлектриком с диэлектрической проницаемостью e₁ и наполовину диэлектриком с диэлектрической проницаемостью e₂ (рис. 8.20). Найдите емкость такого конденсатора. Площадь каждой обкладки S, расстояние между ними d.

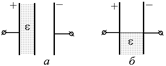Рис. 8.20 Рис. 8.21

В14.Половину oбъема плоского кон­денсатора заполняют диэлек­триком двумя различными спо­собами (рис. 8.21). Нарисуйте картину силовых линий в каж­дом случае и определите, какой из способов выгоднее с точки зрения увеличения емкости.

В15. Между пластинами заряженного плоского конден­сатора ввели диэлектрик с диэлектрической проница­емостью e, так что он полностью заполнил объем между половинами площадей пластин. Во сколько раз измени­лась емкость конденсатора, заряд на пластинах и напря­жение между ними?

В16. Конденсатор, имеющий заряд q, площадь пластины S и расстояние между пластинами d, погружают в керосин на 2/3 его объема. Каково будет напряжение на погруженном конденсаторе? Диэлектрическая проницаемость e.

В17. В заряженном плоском конденсаторе, отсоединен­ном от источника тока, напряженность электрического поля равна Е_о. Половину пространства между пластинами конденсатора заполнили диэлектриком с диэлектрической проницаемостью e (толщина диэлектрика равна расстоянию между пластинами). Найти напряженность электрического поля Е в пространстве между пластинами, свободном от диэлектрика.

В18. Как изменится емкость плоского воздушного конденсатора с обкладками размером а×а и расстоянием d между ними, если в зазор между его обкладками внести металлическую пластину с размерами (a/2)×(а/2) и толщиной d/2 параллельно обкладкам? Изобразите картину силовых линий элек­трического поля в таком конденсаторе.

Задачи трудные

С1. Два плоских воздушных конденсатора с одинаковыми пластинами заряжены одинаковыми зарядами. Расстояние между пластинами у одного конденсатора вдвое больше, чем у другого. Как изменится разность потенциалов между пласти­нами первого конденсатора, если второй конденсатор вставить в первый, как показано на рис. 8.22,а? Как изменится раз­ность потенциалов между пластинами первого конденсатора, если второй конденсатор вставить в первый, как показано на рис. 8.22,б?

Рис. 8.22

С2. Пластины воздушного конденсатора имеют площадь S = 300 см² и удалены друг от друга на расстояние d = 3,0 мм. Между ними находится металлическая пластинка с такой же площадью и толщиной d₁ = 1,0 мм, изолированная от земли. Конденсатор заряжен до напряжения U = 600 В и от­ключен от источника напряжения. Какую работу А надо про­извести, чтобы вытащить пластинку?

С3. Плоский воздушный конденсатор с расстоянием между пластинами d = 5 см и площадью S = 500 см² под­соединен к источнику напряжением U = 2000 В. Параллельно пластинам в конденсатор вводится металлическая плита толщиной d₁ = 1 см. Какую работу А совершает при этом батарея?

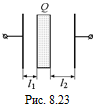С4. В пространство между обкладками незаряженного пло­ского конденсатора вносят металлическую пластину, имеющую заряд Q, так, что между пластиной и обкладками конденсатора остаются зазоры l₁ и l₂ (рис. 8.23). Площади пластины и обкла­док конденсатора одинаковы и равны S. Определите разность потенциалов между обкладками конденсатора.

С5. В плоском конденсаторе одна обкладка имеет заряд +Q₁, а другая +Q₂. Внутрь конденсатора параллельно обкладкам помещают незаряженную металлическую пластину. Какой заряд будет индуцирован на левой и правой поверхностях пла­стины?

С6. Плоский конденсатор с площадью пластины S и расстояни­ем между пластинами d подключен к источнику постоянного напря­жения U. Как изменится заряд на конденсаторе, если в него вве­сти пластинку толщины 2/3 d с диэлектрической проницаемо­стью e?

С7. Пространство между пластинами плоского конден­сатора заполнено двумя слоями диэлектриков: стекла толщиной d₁ = 1,00 см и парафина толщиной d₂ = 2,00 см. Разность потенциалов между обкладками U = = 3000 В. Определить напря­женность поля Е и падение потенциала в каждом из слоев. Диэлектрическая проницаемость стекла e₁ = 7,00, парафина e₂ = 2,00.

С8. Плоский конденсатор, пластины которого рас­положены горизонтально, наполовину залит жидким ди­электриком. Какую часть k аналогичного конденса­тора надо залить жидкостью при вертикальном распо­ложении пластин, чтобы емкости в обоих случаях были одинаковы? Диэлектрическая проницаемость жидкости e.

С9. Плоский конденсатор с расстояни­ем между пластинами d погружается до половины в жидкость с диэлектрической проницаемостью e. На сколько надо раздвинуть пластины, чтобы емкость конденсатора осталась неизменной? Разобрать два случая, указанных на рис. 8.24.

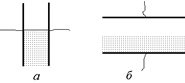
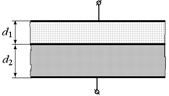
Рис. 8.24 Рис. 8.25

С10. Пространство между обкладками плоского конденсатора заполнено двумя слоями разных диэлектриков толщины d₁ и d₂ (рис. 8.25). Диэлектрическая проницаемость диэлектриков e₁ и e₂. Площадь обкладок S. Найти емкость конденсатора. Какой заряд будет индуцироваться на границе раздела диэлектриков, если на пластинах конденсатора разместить заряд ±q?

С11. Плоский конденсатор, пластины которого заряжены зарядами +q и –q, на половину высоты пластин погружен в жидкость с диэлектрической проницаемостью e. Какова плотность поляризационных зарядов диэлектрика, если площадь пластин S?

С12. В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d внесена парал­лельно обкладкам диэлектрическая пластинка с диэлект­рической проницаемостью e = 2, которая расположена так, как показано на рис. 8.26. Во сколько раз изменится емкость конденсатора при внесении в него пластинки?

Рис. 8.26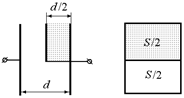 Рис. 8.27

С13. В воздушный конденсатор емкости С₀ вводят пластину с диэлек­трической проницаемостью e, как указано на рис. 8.27. Конденсатор какой емкости надо включить последовательно с данным, чтобы емкость батареи была равна С₀?

С14. Площадь обкладок плоского конденсатора S, расстояние между ними d. Определить:

а) как изменится емкость конденсатора, если между его обкладками поместить металлическую пластину толщины d/3 и площади S?

б) как изменится емкость конденсатора, если между его обкладками поместить металлическую пластину той же толщины d/3, но площади S' < S?

в) изменится ли емкость конденсатора, если эта пластина коснется одной из обкладок?

С15. В плоский конденсатор с площадью обкладок S₁ и расстоянием между ними d₁ помещена диэлектрическая пластинка площади S₂ и толщины d₂. Диэлектрическая проницаемость пластинки e. Найдите емкость конденсатора.