ЕМКОСТЬ СИСТЕМЫ КОНДЕНСАТОРОВ
Вспомним, что при параллельном соединении общая емкость системы, состоящей из N конденсаторов вычисляется по формуле
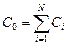 . (9.1)
. (9.1)
Если все емкости Сi одинаковы и равны С, то справедливо
С0 = CN. (9.2)
При последовательном соединении емкость системы конденсаторов вычисляется по формуле
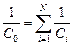 . (9.3)
. (9.3)
Если все емкости Сi одинаковы и равны С, то  , отсюда
, отсюда
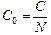 . (9.4)
. (9.4)
СТОП! Решите самостоятельно: А1–А4.
Задача 9.1. Между клеммами А и В включены конденсаторы емкостями С1 = 1 мкФ (точно) и С2 = 2 мкФ (точно) (рис. 9.1). Вычислить емкость системы.
| С1 = 1 мкФ С2 = 2 мкФ |  Рис. 9.1 Рис. 9.1
|
| С0 = ? | |
Решение. Будем вычислять искомую емкость последовательно.
1. Сначала вычислим емкость С' – емкость трех последовательно соединенных конденсаторов (рис. 9.2). Согласно (9.4)
 (мкФ).
(мкФ).
Рис. 9.2 
2. Вычислим емкость С'' как емкость двух параллельно соединенных конденсаторов с емкостями С2 и С':
С'' = С2 + С' = 2 +  (мкФ).
(мкФ).
3. Вычислим емкость С''' как емкость трех последовательно соединенных конденсаторов с емкостями С1, С'' и С1. Согласно формуле (9.3)
 (мкФ).
(мкФ).
4. Вычислим искомую емкость нашей системы как емкость двух параллельно соединенных конденсаторов С2 и С''':
С0 = С2 + С''' = 2 мкФ + 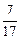 мкФ = 2
мкФ = 2 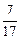 мкФ.
мкФ.
Ответ: С0 = 2 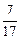 мкФ.
мкФ.
СТОП! Решите самостоятельно: А5, А6, В1, В2, С1, С3.
Задача 9.2. Вычислить емкость системы конденсаторов, показанной на рис. 9.3.
| С | 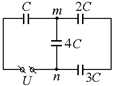 Рис. 9.3
Рис. 9.3
| Решение. Заметим, что конденсаторы 2С и 3С соединены последовательно, а конденсатор 4С подключен к ним параллельно. Поэтому нашу схему можно перерисовать в более наглядном виде (рис. 9.4). А общую емкость такой системы вычислить уже не трудно: |
| С0 = ? | ||
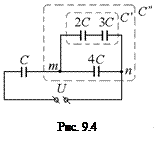
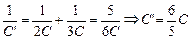 ,
,
 ,
,
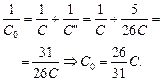
Ответ: 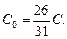
СТОП! Решите самостоятельно: В4 (а, б), С4, D1.
Задача 9.3. В схеме, показанной на рис. 9.5, емкость батареи конденсаторов не изменится при замыкании ключа. Определить Сх.
| С | Решение. Емкость не изменится, если после замыкания ключа все заряды останутся «на своих местах». А для этого необходимо, чтобы потенциалы точек а | |
| Сх = ? | ||
 Рис. 9.5
Рис. 9.5
| и б были равны, т.е. напряжение U1 на конденсаторе Сх должно равняться напряжению на нижнем конденсаторе 2С, а напряжение U2 на верхнем конденсаторе 2С должно равняться напряжению на конденсаторе 4С. Пусть заряды конденсаторов Сх и 2С равны q1, а заряды 2С и 4С – q2. Тогда | |
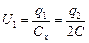 , (1)
, (1)
 . (2)
. (2)
Разделим почленно (1) на (2) и получим
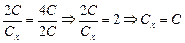 .
.
Ответ: Сх = С.
СТОП! Решите самостоятельно: В5 (а–д).
«Мостик»
Задача 9.4. Определить емкость соединения конденсаторов, изображенного на рис. 9.6
| С1 С2 | Решение. Пусть на клеммы А и В подано напряжение U. Заметим, что в силу симметрии схемы заряды на верхнем и нижнем конден- |  Рис. 9.6
Рис. 9.6
 Рис. 9.7
Рис. 9.7
|
| Собщ = ? | ||
саторах С1 должны быть равны. Но тогда равны и напряжения на этих конденсаторах:
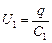 .
Из этого следует, что потенциалы точек т и п равны jт = jп. Значит, конденсатор С3 при включении напряжения заряжаться не будет и распределение зарядов на остальных конденсаторах никак не изменится от того, что мы вообще удалим конденсатор С3 из нашей схемы (рис. 9.7). Емкость такой схемы .
Из этого следует, что потенциалы точек т и п равны jт = jп. Значит, конденсатор С3 при включении напряжения заряжаться не будет и распределение зарядов на остальных конденсаторах никак не изменится от того, что мы вообще удалим конденсатор С3 из нашей схемы (рис. 9.7). Емкость такой схемы
 , ,
|
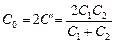 .
.
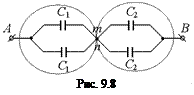
Читатель: Но если потенциалы точек т и п равны мы, наверное, имеем право соединить их в одну (рис. 9.8)?
Автор: Конечно! И если мы подсчитаем емкость получившейся системы, получим тот же результат:
 .
.
Ответ: 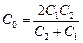 .
.
СТОП! Решите самостоятельно: В6, С6, D2.
Задача 9.5. В проволочный тетраэдр включены конденсаторы так, как показано на рис. 9.9. Найти емкость данной системы.
| С | Решение. Заметим, что грани ADB и АЕВ физически «равноправны», т.е. одна ничем не отличается от другой | |
| С0 = ? | ||
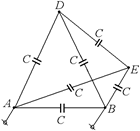 Рис. 9.9 Рис. 9.9
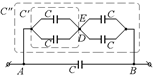 Рис. 9.10
Рис. 9.10
| ни по количеству конденсаторов, ни по порядку их включения.
Из этого следует, что потенциалы точек D и Е равны. А значит, конденсатор на ребре DE заряжаться не будет, и мы можем спокойно удалить его из схемы, а точки D и Е соединить в одну. Тогда нашу схему можно заменить схемой, показанной на рис. 9.10. Емкость этой схемы легко подсчитать:
С' = 2С, 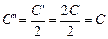 ,
С0 = С + С² = С + С = 2С.
Ответ: С0 = 2С. ,
С0 = С + С² = С + С = 2С.
Ответ: С0 = 2С.
| |
СТОП! Решите самостоятельно: С7, С8, D3, D4.
Дата добавления: 2016-04-11; просмотров: 16343;
