Общий случай расчета емкости системы

Задача 9.7. Определите емкость системы конденсаторов, изображенной на рис. 9.14.

С	Решение. Очевидно, что в данном случае потенциалы точек а и b не равны, поэтому удалять конден-	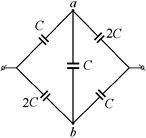Рис. 9.14
С0 = ?
сатор, включенный между этими точками, нельзя. Подадим на клеммы системы напряжения U, тогда все конденсаторы приобретут заряды (рис. 9.15). Из симметрии схемы следует, что заряды обоих конденсаторов С будут одинаковы, обозначим их

q₁. Заряды обоих конденсаторов 2С также будут одинаковы, обозначим их q₂. Заряды на пластинах конденсатора С между точками а и b обозначим q₃.

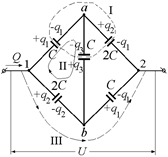Рис. 9.15

Мы взяли заряд верхней пластины –q3, а нижний +q3. (Могли взять и наоборот.) Если в итоге получится q3 > 0, значит, мы не ошиблись в знаках, а если получится q3 < 0, то нижняя пластина на самом деле заряжена отрицательно, а верхняя положительно. Общий заряд Q, поступивший в систему, равен Q = q1 + q2. Наша искомая емкость

.

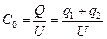Следовательно, чтобы найти С₀, надо выразить сумму q₁ + q₂ через величины С и U.

Заметим, что единый проводник, обведенный пунктиром (линия I на рис. 9.15) электрически нейтрален, поэтому справедливо

–q₁ + q₂ – q₃ = 0. (1)

Вспомним, что если перенести единичный положительный заряд с положительно заряженной пластины конденсатора на отрицательно заряженную, электрическое поле конденсатора совершит положительную работу, численно равную U = q/C (рис. 9.16,а).

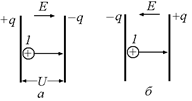Рис. 9.16

А если перенести единичный положительный заряд с отрицательно заряженной пластины на положительную, то электрическое поле конденсатора совершит отрицательную работу, численно равную –U = –q/C (рис. 9.16,б).

Если переместить заряд по замкнутому контуру II (см. рис. 9.15), то суммарная работа сил электрического поля будет равна нулю:

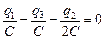. (2)

Переместим единичный положительный заряд по линии III из точки 1 в точку 2 (см. рис. 9.15). Тогда общая работа сил поля будет равна напряжению U:

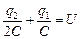. (3)

Теперь решим систему уравнений (1)–(3) относительно неизвестных величин q₁, q₂, q₃:

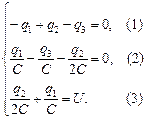
Из (1) получим q₃ = q₂ – q₁. Подставим значение q₃ в (2):

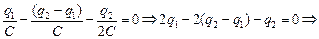
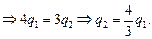
Подставим значение q₂ в (3):

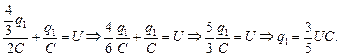
Тогда .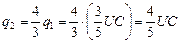

Заряд Q, поступивший от источника на пластины системы конденсаторов равен

.

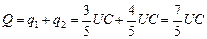И, наконец, искомая емкость нашей системы равна

С₀ = .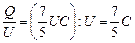

Ответ получен и задача решена. Теперь давайте вычислим q₃:

.

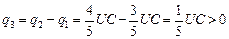Значит, знаки зарядов обкладок конденсатора С, включенного между точками а и b (см. рис. 9.15), мы угадали верно!

Ответ: .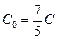

СТОП! Решите самостоятельно: С14, D7, D8.