Плоскопараллельной пластины? Задача 5.1.На какое расстояние сместится луч, проходящий через плоскопараллельную пластинку, если толщина ее d,показатель преломления п

Задача 5.1.На какое расстояние сместится луч, проходящий через плоскопараллельную пластинку, если толщина ее d,показатель преломления п, а угол падения луча i? Может ли смещение луча быть больше толщины пластинки?

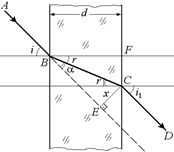Рис. 5.7

1. Если i – угол падения, а r – угол преломления, то согласно закону преломления

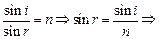
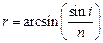. (1)

2. Рассмотрим прямоугольный DBFC. В нем BF = d – толщина пластинки, а ВС – траектория луча внутри пластины, при этом справедливо

. (2)

3. Теперь рассмотрим прямоугольный DВСЕ. Как видно из рис. 5.7, Ða = Ði – Ðr, тогда .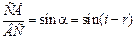

Подставляя в последнее равенство ВС из (2) и учитывая, что СЕ = х, получим

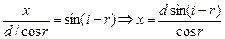. (3)

Подставляя в формулу (3) значение угла r из (1), получим окончательное выражение для х:

.

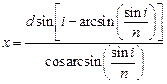Читатель: А нельзя ли как-нибудь «избавиться» от арксинусов? А то уж очень все громоздко.

Автор: При большом желании можно, хотя совершенно необязательно. Для этого преобразуем формулу (3):

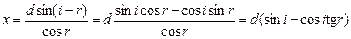. (4)

Мы знаем, что ,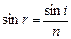

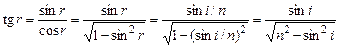. (5)

Подставим выражение для tgr из (5) в (4) и получим

.

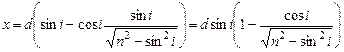Если такое выражение нравится Вам больше, можно взять его в качестве ответа на первый вопрос задачи. Осталось ответить на второй вопрос: может ли смещение луча х быть больше толщины пластинки d? Из рис. 5.7 видно, что чем больше угол падения i, тем больше смещение х. При i = 90°

.

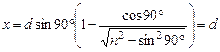Поэтому максимальное значение смещения луча достигает в случае, когда луч падает на пластинку как бы по касательной к ее поверхности.

Ответ: .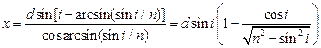

СТОП! Решите самостоятельно: В10–В12, С5, D2.