Монета на дне стакана
Положим на дно стакана монету, а потом наполним стакан водой и посмотрим на монету сверху (рис. 5.10). Мы увидим, что монета находится несколько выше, чем она находилась до того, как налили воду. (В том, что это действительно так, Вы легко можете убедиться экспериментально!)
Рис. 5.10
|
Для того чтобы понять, почему это так, рассмотрим ход лучей АВ иАС,идущих к наблюдателю от монеты. На границе вода–воздух эти лучи испытают преломление, причем угол преломления будет больше угла падения. Как видно из рис. 5.10, продолжения преломленных лучей пересекаются в некоторой точке А¢, расположенной над монетой (точкой А). Человеческий глаз воспринимает эти лучи так, как если бы они исходили из точки А¢, хотя в точке А¢ находится не монета, а мнимое изображение монеты.
СТОП! Решите самостоятельно: А5–А7, В17, В18, С8, С9.
Читатель: А можно ли вычислить, на какой глубине находится мнимое изображение монеты?
Автор: Конечно! Пусть высота столба воды в стакане равна Н = OS (рис. 5.11). Найдем расстояние от поверхности воды до мнимого изображения h = OS¢.
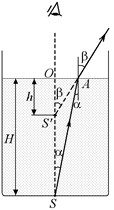Рис. 5.11
|
Рассмотрим прямоугольные треугольники AS¢O и ASO.
из D ASO: АО = Нtga, (1)
из D AS¢O: АО = htgb. (2)
Из закона преломления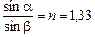 
.
Приравняем правые части равенств (1) и (2), получим
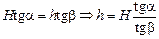. (3)
Поскольку углы a и b в условии данной задачи малы, то tgb » sinb, tga » sina. Тогда равенство (3) примет вид
.
Запомним:
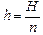. (5.1)
То есть мы видим мнимое изображение предмета, лежащего на дне, на глубине Н/п от поверхности воды.
СТОП! Решите самостоятельно: А8, А9, В19, С10.
Задача 5.4. Пловец, нырнувший с открытыми глазами, рассматривает из-под воды светящийся предмет, находящийся над его головой на расстоянии l = 75 см над поверхностью воды. Каково будет видимое расстояние предмета над поверхностью воды? Показатель преломления воды п = 4/3.
| l = 75 см n = 4/3 | Решение. Рассмотрим два луча, идущие из светящегося предмета (точка S) в глаз пловца (рис. 5.12). Пусть первый луч SO идет перпендикулярно поверхности воды, а луч SA падает на поверхность воды под малым |
| l1= ? | |
углом a и, преломившись, идет в воде в направлении АВ. При этом угол падения a и угол преломления b связаны соотношением
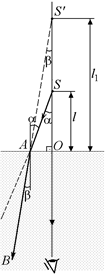Рис. 5.12
|
.
Продолжения лучей SO и АВ пересекаются в точке S¢, которая является мнимым изображением источника S. Именно в точке S¢ пловец увидит светящийся предмет.
Найдем расстояние l1. Из треугольников AS¢O и ASO можем записать:
АО = ltga = l1tgb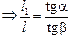 
.
С учетом малости углов a и b принимаем tgb » sinb, tga » sina, тогда
.
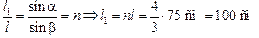Ответ: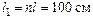 
.
СТОП! Решите самостоятельно: В20, С11.
Дата добавления: 2016-04-11; просмотров: 6303;