Монета на дне стакана. Линза и плоскопараллельная пластина

Линза и плоскопараллельная пластина

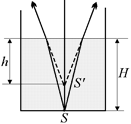Рис. 12.1

Если положить монету на дно стакана, наполненного водой, то, как мы уже выяснили в § 5, слой воды создаст мнимое изображение монеты, которое будет находиться над монетой на глубине 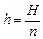(рис. 12.1), где Н – толщина слоя воды, а п – показатель преломления воды.

Задача 12.1. Сосуд заполнен водой. Толщина слоя воды Н = = 18 см. Над поверхностью воды вплотную к воде расположена стеклянная плосковыпуклая линза радиусом R = 10 см (рис. 12.2). На дне сосуда находится точечный источник света S. Где находится изображение источника? Показатель преломления воды п₁ = 1,3, стекла п₂ = 1,5.

Н = 18 см R = 10 см п1 = 1,3 п2 = 1,5	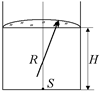Рис. 12.2 Рис. 12.3
х = ?

Решение. Сначала мысленно уберем линзу. Тогда лучи будут выходить из воды так, как если бы они исходили из точки S¢ (рис. 12.1), расположенной на глубине: 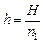. Значит, мы можем считать, что на линзу падает пучок лучей, исходящий из точечного источника S¢ (рис. 12.3). Тогда мы можем записать формулу линзы

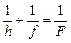, (1)

где

Подставляя значения 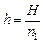и 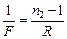в формулу (1), получим

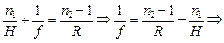
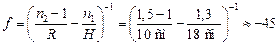см.

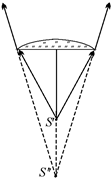Рис. 12.4

То есть линза дает мнимое изображение S², расположенное на расстоянии | f | = 45 см перед плоскостью линзы (рис 12.4).

Читатель: Меня несколько смущает одно место в ваших рассуждениях: когда мы определяли глубину «залегания» мнимого изображения в § 5, мы предполагали, что лучи из воды выходят в воздух. А в нашем случае они выходят непосредственно в стекло. Ведь между поверхностью воды и линзой нет воздушной «прослойки».

Автор: Вы правы. Но дело в том, что ход луча на границе «вода–стекло» при наличии воздушной прослойки будет точно таким же, как и при ее (прослойки) отсутствии. Покажем это.

Рассмотрим ход произвольного луча, идущего из воды в стекло через воздушную прослойку (12.5, а) и из воды в стекло непосредственно (рис. 12.5, б).

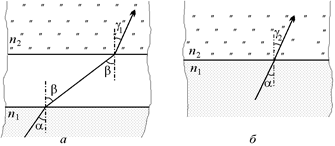
Рис. 12.5

Пусть в обоих случаях луч выходит из воды с углом падения a. Тогда, используя закон преломления света, можем записать:

в первом случае:

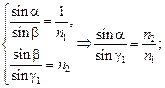(2)

во втором случае:

(3)

Сравнивая выражения (2) и (3), можем утверждать, что g₁ = g₂, т.е. наличие воздушной прослойки никак не повлияет на направление луча в стекле.

СТОП! Решите самостоятельно: В1, С1.