Светлое пятно на дне водоема

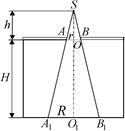Рис. 12.22 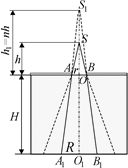  Рис. 12.23

Автор: Рассмотрим такую ситуацию: точечный источник света находится над пустым сосудом. Поверхность сосуда закрыта непрозрачным экраном, и в этом экране точно под источникам света сделано отверстие радиусом r (рис. 12.22). Расстояние от источника до сосуда h, глубина сосуда Н. Каким будет радиус светлого пятна на дне сосуда?

Читатель: Радиус R легко найти из подобия треугольников SAO и SA₁О₁:

.

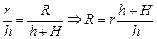Автор: Совершенно верно. А если в сосуд налить воды?

Читатель: Тогда получается как бы фонарик над бассейном, а слой воды создает мнимое изображение источника на высоте h₁ = пh согласно формуле (12.2). В этом случае радиус светлого пятна можно найти из подобия треугольников S₁AO и S₁A₁О₁ (рис. 12.23):

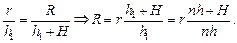
Автор: Правильно. А если мы поместим в отверстие рассеивающую линзу?

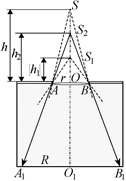Рис. 12.24

Читатель: Рассеивающая линза дает мнимое изображение в точке S₁. Высоту |h₁| этого изображения над линзой можно найти по формуле линзы: 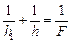, где h₁ < 0, F < 0, а h > 0 (рис. 12.24). Вода будет «воспринимать» лучи, падающие на нее сверху так, как если бы они исходили из точки S₁. Тогда слой воды будет давать мнимое изображение S₂ мнимого источника S₁ на высоте h₂ = = n|h₁| согласно формуле (12.2). А зная высоту h₂ уже легко найти радиус светлого пятна из подобия треугольников S₂AO и S₂А₁О₁:

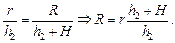
СТОП! Решите самостоятельно: С7, С8.

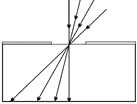Рис. 12.25

Автор: С точечным источником над водой мы разобрались. А вот каким будет радиус светлого пятна, если на поверхность сосуда, накрытого непрозрачным экраном с круглым отверстием, будет падать рассеянный свет? Сначала рассмотрим ситуацию, когда в сосуде нет воды (рис. 12.25).

Читатель: По-моему, в этом случае никакого светлого пятна с четкими границами на дне не получится: вся поверхность дна будет освещена, так как при рассеянном свете лучи будут падать на отверстие под всевозможными углами. Хотя, конечно, освещенность различных участков дна будет разной.

Автор: Вы правы. А что изменится, если сосуд заполнить водой?

Читатель: Тогда самая дальняя от центра О₁ на дне «светлая» точка будет определяться лучом АВ, падающим на поверхность воды почти по касательной к поверхности воды (рис. 12.26). Угол преломления a₀ этого луча определяется из закона преломления:

.

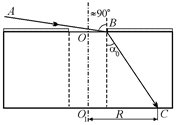
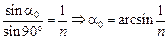Автор: Совершенно верно!

Рис. 12.26

СТОП! Решите самостоятельно: С9.