Изображение в плоскопараллельной пластине

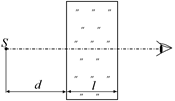Рис. 12.15

Расположим перед плоскопараллельной стеклянной пластиной точечный источник света S (рис. 12.15) и определим, в каком месте увидит источник наблюдатель, находящийся за пластиной.

Построим ход произвольного луча SА, падающего из источника S на пластину (рис. 12.16). Он испытает два преломления в точках А и В и выйдет из пластины в направлении D.

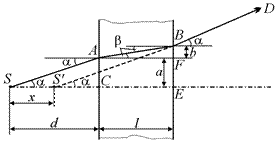Рис 12.16

Луч BD после преломления идет так, как если бы он исходил из точки S¢, т.е. в точке S¢ находится мнимое изображение источника S, причем это изображение находится ближе к пластине, чем источник, на некоторое расстояние х.

Если нам известна толщина пластины l и ее показатель преломления п, а также расстояние d от источника до пластины, то мы сможем определить величину х.

Так, если угол a – угол падения, а угол b – угол преломления, то, считая оба угла малыми, можем записать:

a/b = п. (1)

Обозначим для краткости: BF = b, EF = a.

Сначала определим S¢Е – расстояние от мнимого изображения до задней грани пластины.

Из DS¢BE:

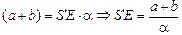, (2)

из DSAC:

а = d×a, (3)

из DABF:

b = l×b. (4)

Подставляя (3) и (4) в (2), получим:

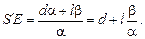
А с учетом равенства (1)

.

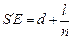Теперь найдем искомую величину х. Как видно из рис. 12.16,

.

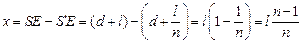Запомним:

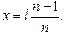(12.3)

Заметим, что величина х не зависит от величины d – расстояния от источника до пластины, а зависит только от толщины l и показателя преломления п пластины.

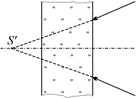Рис. 12.17

Читатель: А если на плоскопараллельную пластину падает сходящийся пучок лучей (рис. 12.17)?

Автор: Если мы на рис. 12.16 обратим луч SABD вспять, то получим в точке S действительное изображение. Причем действительное изображение S будет смещено от мнимого источника S¢ на расстояние х, которое мы уже определили: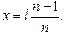

Задача 12.4. Перед собирающей линзой с фокусным расстоянием F = 10 см на расстоянии d = 20 см расположен точечный источник света. За линзой на расстоянии а = l от нее находится плоскопараллельная стеклянная пластина толщиной l = 3 см (рис. 12.18). Показатель преломления стекла п = 1,5. Где находится изображение?

F = 10 см d = 20 см а = l l = 3 см п = 1,5	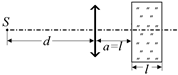Рис. 12.18 Решение. Будем решать задачу по частям. Сначала забудем про стеклянную пластину: оставим только точечный источник и линзу (рис. 12.19).
у = ?

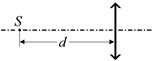Рис. 12.19 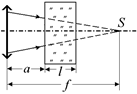  Рис. 12.20

Найдем положение изображения по формуле линзы:

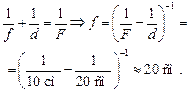
Теперь рассмотрим плоскопараллельную пластину, параллельную линзе, на которую падает сходящийся пучок лучей. Поскольку f > a + l, то продолжения падающих лучей пересекутся за пластиной (рис. 12.20).

Как мы уже выяснили, в этом случае действительное изображение будет смещено относительно мнимого источника на расстояние 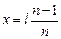(рис. 12.21).

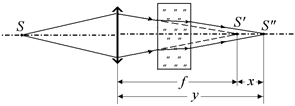Рис. 12.21

Поэтому действительное изображение источника получится за плоскостью линзы на расстоянии

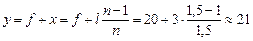см.

Ответ: на расстоянии 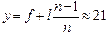см за плоскостью линзы, где .

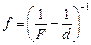СТОП! Решите самостоятельно: В5, С5, С6.