Мнимый источник под водой
Рассмотрим такую ситуацию: на поверхность воды падает сходящийся пучок лучей, такой, что если бы на его пути воды не было, то он бы сфокусировался в точке S, находящейся на глубине h под поверхностью воды (рис. 12.6). Возникает вопрос: где сфокусируется данный пучок при наличии воды?
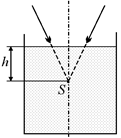 Рис. 12.6
Рис. 12.6 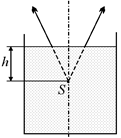 Рис. 12.7
Рис. 12.7
Читатель: По-моему, здесь можно воспользоваться принципом обратимости световых лучей. Пустим мысленно лучи в противоположном направлении. Тогда они будут выходить из воды так, как если бы они исходили из точки S (рис. 12.7), т.е. точка S будет мнимым изображением, которое образует слой воды.
Обратимся к рис. 12.1. Чтобы лучи, выходящие из воды, образовали мнимое изображение на глубине h, они должны исходить из действительного источника, расположенного на глубине Н, причем 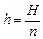 , а значит, Н = nh.
, а значит, Н = nh.
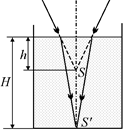 Рис. 12.8
Рис. 12.8
|
Теперь вернемся к нашей ситуации. Лучи должны после преломления на границе «воздух–вода» идти так, чтобы сфокусироваться в точке S1, расположенного на глубине Н (рис. 12.8). При этом
Н = nh. (12.1)
Автор: Совершенно верно!
Задача 12.2. Над поверхностью воды на высоте h = 5,0 см находится собирающая линза с фокусным расстоянием F = 10 см (рис. 12.9, а). На линзу сверху падает параллельный пучок лучей. Найти точку, в которой сфокусируются лучи. Показатель преломления воды п = 1,33.
а  б
б 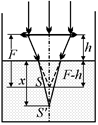
Рис. 12.9
| h = 5,0 см F = 10 см п = 1,33 | Решение. Если бы за линзой не было воды, то после преломления все лучи пересеклись бы в главном фокусе линзы на расстоянии F = 10 см за линзой (рис. 12.9, б). Получается, что на поверхность воды падает сходящийся пучок лучей. Тогда получается |
| х = ? | |
ситуация, изображенная на рис. 12.8, а значит, лучи сфокусируются в точке S¢, расположенной на глубине п(F – h). Тогда искомая величина х равна:
х = п(F – h) = 1,33×(10 – 5,0) » 6,7 см.
Ответ: х = п(F – h) » 6,7 см.
СТОП! Решите самостоятельно: В2, В3, С2.
Дата добавления: 2016-04-11; просмотров: 802;
