Линза и сферическое зеркало

Задача 14.1. Определить положение изображения, даваемого оптической системой, состоящей из вогнутого зеркала с фокусным расстоянием 10 см и собирающей линзы с фокусным расстоянием 20 см (рис. 14.1). Расстояние от зеркала до линзы 30 см, от линзы до предмета 40 см. Все значения точные. Провести графическое построение изображения.

F1 = 10 см F2 = 20 см а = 30 см d = 40 см	Рис. 14.1
f = ?

Решение. Будем решать задачу последовательно. Сначала найдем положение изображения в линзе так, как если бы никакого зеркала вообще не было. Применим формулу линзы:

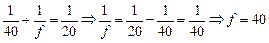см.

Это значит, что на вогнутое зеркало падает сходящийся пучок лучей, который сфокусировался бы в точку S₁ на расстоянии 10 см за зеркалом, если бы зеркала на пути не было бы (рис. 14.2).

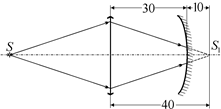Рис. 14.2

Иными словами, на расстоянии 10 см за вогнутым зеркалом находится мнимый источник S₁.

В § 3 мы уже получили формулу сферического зеркала

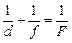, (14.1)

где: d > 0, если источник действительный;

d < 0, если источник мнимый;

f > 0, если изображение действительное;

f < 0, если изображение мнимое;

F = +R/2 – если зеркало вогнутое (R – радиус зеркала);

F = –R/2 – если зеркало выпуклое.

Применим формулу (14.1) к нашему случаю: источник мнимый, поэтому d = –10 см, зеркало вогнутое, поэтому F = +10 см. Получим:

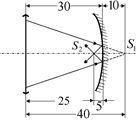Рис. 14.3

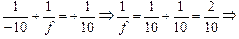
f = 5 см > 0.

Значит, зеркало дает действительное изображение S₂, расположенное на расстоянии 5 см перед поверхностью зеркала. Это изображение является для линзы действительным источником, расположенным на расстоянии d₁ = 30 – 5 = 25 см перед плоскостью линзы (рис. 14.3).

Еще раз применим формулу линзы:

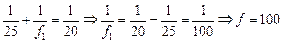см,

т.е. после второго преломления в линзе лучи сфокусируются на расстоянии 100 см слева от линзы (рис. 14.4).

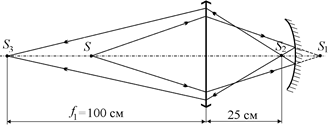
Рис. 14.4

Ответ: система дает два действительных изображения: на расстоянии 25 см справа от линзы и на расстоянии 100 см слева от линзы.

СТОП! Решите самостоятельно: В1, С1.