Посеребрённая линза
Рассмотрим такую оптическую систему: вплотную к сферическому зеркалу приложили линзу (рис. 14.11). Проще всего создать такую систему, нанеся на одну из поверхностей линзы отражающий слой. Например, можно покрыть поверхность линзы тонким слоем серебра.
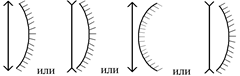 Рис. 14.11
Рис. 14.11
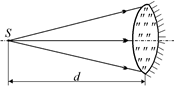 Рис. 14.12
Рис. 14.12
|
Пусть на тонкую посеребрённую линзу падает пучок света от точечного источника (рис. 14.12). Возникает вопрос: как, зная фокусное расстояние линзы F, фокусное расстояние сферического зеркала F¢ и расстояние от предмета до зеркала d, определить, где будет находиться изображение и каким это изображение будет (действительным или мнимым)?
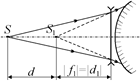
Попробуем ответить на этот вопрос в общем виде для любого сочетания линзы и зеркала, показанных на рис. 14.11, и для любых величин d, F и F¢. Будем рассуждать последовательно. Пусть на систему «линза–зеркало» падает пучок лучей от точечного источника S. Если бы зеркала не было, линза дала бы изображение S1: действительное f1 > 0 (рис. 14.13,а) или мнимое f1 < 0 (рис. 14.13,б). В обоих случаях справедлива формула линзы:
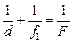 . (1)
. (1)
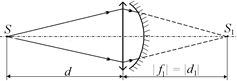
а б
Рис. 14.13
Зеркало воспринимает преломленный линзой пучок лучей так, как если бы они имели своим источником точку S1. В первом случае S1 – мнимый источник для вогнутого зеркала, а во втором – действительный источник для выпуклого зеркала. При этом расстояние |d1| от нового источника до зеркала равно | f1|.
Заметим, что в обоих случаях d1 = –f1.
В первом случае f1 > 0, d1 < 0 Þ d1 = –f1.
Во втором случае f1 < 0, d1 > 0 Þ d1 = –f1.
Запишем формулу сферического зеркала
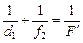 , (2)
, (2)
где F¢ – фокусное расстояние зеркала, которое может быть как положительным (см. рис. 14.13, а), так и отрицательным (см. рис. 14.13, б). С учетом того, что d1 = –f1, уравнение (2) можно записать так:
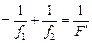 . (3)
. (3)
Линза воспримет отраженный от зеркала пучок лучей так, как если бы этот пучок либо сходился бы в мнимый источник S2 (рис. 14.14, а), либо исходил из действительного источника S2 (рис. 14.14, б). Таким образом, величина | f2| – это расстояние от нового источника S2, созданного зеркалом, до линзы: |d2| = | f2|.
а 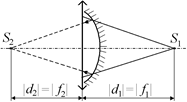
| б 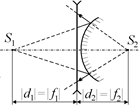
|
Рис. 14.14
В первом случае f2 > 0, d2 < 0 Þ d2 = –f2.
Во втором случае f2 < 0, d2 > 0 Þ d2 = –f2.
После второго преломления в линзе лучи сфокусируются в некоторой точке S3, которая и будет искомым изображением источника S в данной оптической системе (рис. 14.15).
Как видно из рис. 14.15, в случае а – это изображение действительное, а в случае б – мнимое.
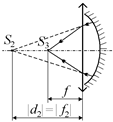 а
а
| 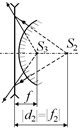 б
б
| Запишем формулу линзы для второго преломления:
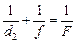 . (4)
С учетом того, что d2 = –f2, уравнение (4) перепишем в виде: . (4)
С учетом того, что d2 = –f2, уравнение (4) перепишем в виде:
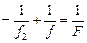 . (5) . (5)
|
| Рис. 14.15 |
Теперь еще раз выпишем и объединим в одну систему уравнения (1), (3) и (5):
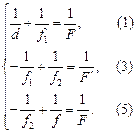
Сложим эти уравнения и получим:
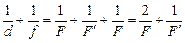 .
.
Запомним полученную формулу:
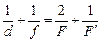 . (14.2)
. (14.2)
Заметим, что если ввести обозначение
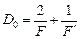 , (14.3)
, (14.3)
то формула (14.2) примет вид
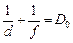 . (14.4)
. (14.4)
Данная формула похожа на формулу сферического зеркала (14.1) с той лишь разницей, что для обычного сферического зеркала оптическая сила 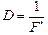 , а для оптической системы «линза–зеркало» оптическая сила
, а для оптической системы «линза–зеркало» оптическая сила
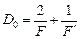 ,
,
где F¢ – фокусное расстояние зеркала, а F – фокусное расстояние линзы. Это значит, что «посеребрённая» линза ведет себя точно так же, как сферическое зеркало, оптическая сила которого определяется по формуле (14.3), при этом фокусное расстояние такого зеркала равно 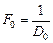 .
.
Задача 14.3. В вогнутое зеркало радиусом R = 16 см налит тонкий слой воды (показатель преломления воды п = 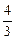 ). Определить фокусное расстояние F0 этой системы. (Все значения точные.)
). Определить фокусное расстояние F0 этой системы. (Все значения точные.)
R = 16 см
п = 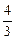
| Решение. У нас получилась система из плосковыпуклой линзы и вогнутого зеркала радиусом R (рис. 14.16). Фокусное расстояние плосковыпуклой линзы определяется по формуле
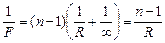 . .
|
| F0 = ? | |
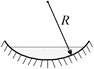 Рис. 14.16
Рис. 14.16
|
Фокусное расстояние вогнутого зеркала
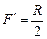 .
.
Согласно формуле (14.3) оптическая сила системы равна
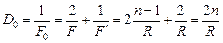 ,
, 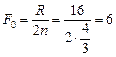 см.
см.
Ответ: 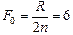 см.
см.
СТОП! Решите самостоятельно: В3, В4.
Задача 14.4. На плоском зеркале лежит линза с фокусным расстоянием 40 см (рис. 14.17). Какова оптическая сила этой системы?
| F = 40 см | Решение. Плоское зеркало – это частный случай сферического зеркала, у которого радиус R ® ¥. Ясно, что и фокусное расстояние плоского зеркала F¢ ® ¥, ведь параллельный пучок лучей, |
| F0 = ? | |
 Рис. 14.17
Рис. 14.17
|
отраженных от плоского зеркала, остается параллельным и никогда не сфокусируется в одну точку. Воспользуемся формулой (14.3):
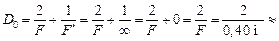 5,0 дптр.
5,0 дптр.
Ответ: 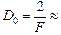 5,0 дптр.
5,0 дптр.
СТОП! Решите самостоятельно: А1, В5, С4, С5.
Задача 14.5. Двояковыпуклая линза имеет фокусное расстояние F = 10 см. Одну из поверхностей линзы, имеющую радиус кривизны R = 10 см, покрыли тонким слоем серебра. Найти положение изображения, которое образует посеребренная линза, если предмет расположить на расстоянии а = 15 см от нее.
| F = 10 см R = 10 см а = 15 см | Решение. Найдем оптическую силу данной системы по формуле (14.3):
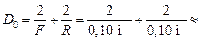 40 дптр. 40 дптр.
|
| f = ? | |
Теперь рассмотрим оптическую систему «линза–зеркало» как вогнутое зеркало с оптической силой D0 = 40 дптр. Применим формулу сферического зеркала:
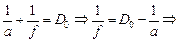
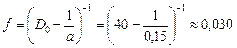 м = 3,0 см > 0.
м = 3,0 см > 0.
Ответ: изображение действительное, находится на расстоянии f = 3,0 см перед линзой.
СТОП! Решите самостоятельно: В6, В7, С6, С7.
Задача 14.6. Плоская поверхность плоско-выпуклой линзы с фокусным расстоянием F покрыта хорошо отражающим слоем. На расстоянии а от линзы со стороны выпуклой поверхности расположен точечный источник света (рис. 14.18). Определить положение изображения. При каких значениях а изображение будет действительным и при каких мнимым?
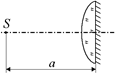 Рис. 14.18
Рис. 14.18
| ||
| F а | Решение. Вычислим оптическую силу данной оптической системы. Для этого запишем формулу (14.3) в виде: D0 = 2Dл + Dз, | |
| f = ? | ||
где Dл = 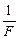 – оптическая сила линзы, Dз – оптическая сила зеркала. С учетом того, что оптическая сила плоского зеркала равна нулю (Dз = 0), получим
– оптическая сила линзы, Dз – оптическая сила зеркала. С учетом того, что оптическая сила плоского зеркала равна нулю (Dз = 0), получим
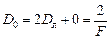 .
.
Теперь применим формулу сферического зеркала:
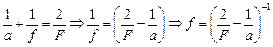 .
.
Если f > 0, то изображение действительное:
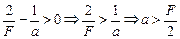 .
.
Если f < 0, то изображение мнимое:
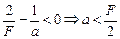 .
.
Ответ: изображение действительное и находится на расстоянии 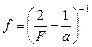 перед линзой, если
перед линзой, если 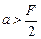 ; изображение мнимое и находится на расстоянии
; изображение мнимое и находится на расстоянии 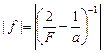 за линзой, если
за линзой, если 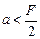 .
.
СТОП! Решите самостоятельно: А2, В8, С8.
Дата добавления: 2016-04-11; просмотров: 7805;
