Преломление с отражением
Задача 5.5. У плоскопараллельной пластинки, имеющей толщину d = l,2 см, задняя поверхность посеребрена. Точечный источник света расположен на расстоянии l = 1,5 см от передней поверхности пластинки. На каком расстоянии L от источника находится его изображение, получающееся в результате отражения лучей от задней поверхности пластинки? Показатель преломления материала пластинки п = 1,6. Луч зрения перпендикулярен к поверхности пластинки.
| l = 1,5 см n = 1,6 d = l,2 см | Решение. Рассмотрим два луча, исходящие из светящегося предмета (точка S) (рис. 5.13). Первый луч SВ падает на пластину перпендикулярно к ее поверхности, отражается в точке C от задней поверхности и возвращается обратно по той же траектории. |
| l = ? | |
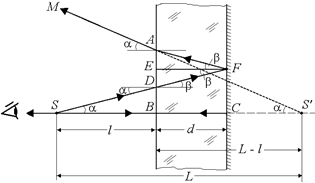 Рис. 5.13
Рис. 5.13
Второй луч SD падает на пластину под малым углом падения a, входит в пластину с углом преломления b, отражается в точке F от посеребренной грани пластины, доходит до точки А, еще раз преломляется на границе «стекло–воздух» и выходит из пластины под углом a к нормали в направлении АМ.
Продолжения двух отраженных лучей АМ и BS, вышедших из пластины, пересекаются в точке S¢, которая является мнимым изображением точки S. Наша задача состоит в том, чтобы найти расстояние SS¢ между источником и мнимым изображением (см. рис. 5.13).
Рассмотрим прямоугольный треугольник ABS¢:
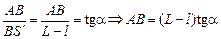 . (1)
. (1)
С другой стороны,
АВ = АЕ + ED + BD.
Из DAFE и DDFE имеем АЕ = ED = dtgb, а из DBDS получаем BD = ltga, тогда
АВ = dtgb + dtgb + ltga = 2dtgb + ltga. (2)
Приравнивая правые части равенств (1) и (2), получим
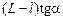 = 2dtgb + ltga Þ
= 2dtgb + ltga Þ
 . (3)
. (3)
Учитывая малость углов a и b, принимаем tgb » sinb, tga » » sina, тогда
 . (4)
. (4)
Подставляя (4) в (3), получим окончательно
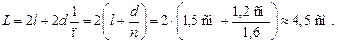
Ответ: 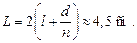
СТОП! Решите самостоятельно: В21.
Дата добавления: 2016-04-11; просмотров: 2556;
