Отражение и преломление электромагнитных волн на границе раздела двух диэлектриков.

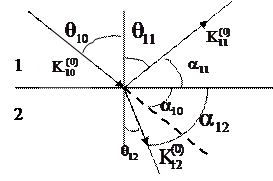Пусть две диэлектрические среды разде­лены плоской границей на со стороны 1 среды падает элек­тромагнитная волна. На гра­нице эта волна частично отра­жается в 1среду, а частично преломится и пройдет во 2. Т. об. В 1 среде присутствует ото­браженная и падающая волны, во 2 – преломленная волна.

Обозначим величины падающая волны индексами 10, отраженной – 11, преломления 12.

Тогда для напряжения электрического поля можно записать:

для падающей волны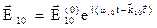

для отраженной волны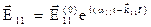

для преломленной волны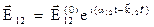

Аналогичный вид имеют вектора напряж. для магнит. поля волны.

Граничные условия непрерывности вектора составляющих имеют вид:

+ =

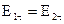
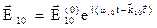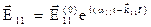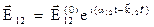
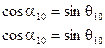(м)

Подставляя (м) в (n)

Получим

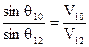
Учитывая выражение для скорости 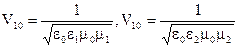, получим

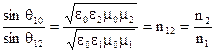
т.е. отношение синуса угла падения к синусу угла преломления равно показателю преломления 2 среды отн-но (1)

(Закон Снеллиуса )

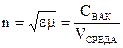показателем преломления (абс.) показыв. насколько С_вак>V_среда 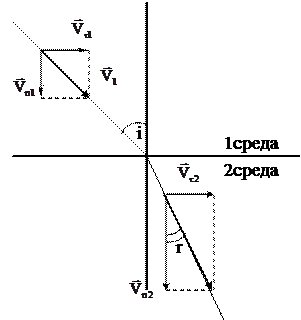оста­ется неизменной 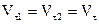. Ньютон объ­яснил изменение V_n “втягиванием” лучей в среду на основных данных n<i:

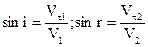
Следовательно:

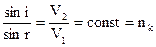
Закон преломления был впервые установлен голландским ученым В. Снеллиусом (1580-1626) и Р. Декартом (1596-1650).

4.3 Принцип Гюйгенса и его применение к явлениям отражения и преломления световых волн

Принцип Гюйгенса: каждая точка среды, до которой доходит световые возбуждения, является источником вторичных световых волн, огибающая которых в данный момент времени является фрон­том (поверхностью) волны; направление распространения волны перпендикулярно волновой фронтовой поверхности.

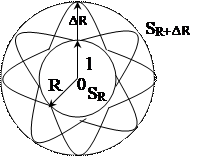Пример: симметричные сфериче­ские световые волны. перво­начальная точка 0 является источником возбужде­ния волн. Если волна распространяется со скоростью V, то через промежуток времени t фронт достигнет поверхности сферы S_R, отстоящей на расстояние R=Vt от точки 0.

За дополнительный промежуток времени ------S_R возбуждение распространяется на расстояние

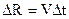
и образует новую пов-ть 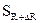, которая является огибающей сфер радиуса .

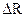Если в рассмотренном случае 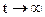, то и 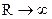, а это означает, что поверхность фронта – к плоской поверхности. В силу этого свойства точечные источники, за которые принимают и далекие звезды, а также Солнце, посылают на Землю световые волны, которые можно считать плоскими.

2. Отражение света.

Пусть плоская волна, фронт которой ОА, соотв моменту времени t, падает на плоскую поверхность и отражается от нее.

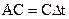Фронтовая поверхность ВС соотв моменту времени . За время , луч 3 пройдет путь , а луч 1 отразится от SS и пройдет путь 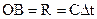. Следовательно ОВ=АС , т.е. пути лучей при переходе на другую волновую поверхность одинаковы.

Лекция 2.

3 Преломление света.

Пусть лучи 1,2,3 преломляются внутрь среды II. Тогда ОА фронт падающей волны; ВС фронт преломленной волны. Луч 3 коснется поверхности SS на время 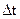позже луча 1. За это время ( 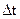) луч 1 пройдет путь 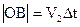, а луч 3 путь 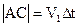. Из 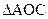следует соотношение 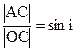. Из 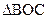соотношение 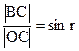. Тогда 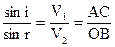или 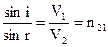, где n₂₁=const для данных сред. Необходимо обратить внимание на то, что здесь n₂₁ обратно тому, которое получено из корпускулярных представлений. Фуко в 1851 году измерил n₂₁ для сред: воздух – вода и показал, что n₂₁>1. Т.е. доказана справедливость волновых представлениях об оптике.

Явление полного внутреннего отражения света.

Опр.1 Абсолютным показателем преломления среды называется величина n, равная отношению скоростей с электромагнитных волн в вакууме к их фазовой скорости в среде:

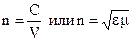
где 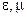- электрическая и магнитная проницаемость среды.

Тогда, относительный показатель преломления n₂₁ может быть в виде: 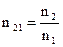, (1.3)

а закон преломления света 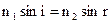(1.4)

Из симметрии выражения (1.4) вытекает обратимость световых лучей.

Обратим луч 1, заставив его падать под углом r, то и преломленный луч будет в I среде распространятся под углом i, т.е. пойдет

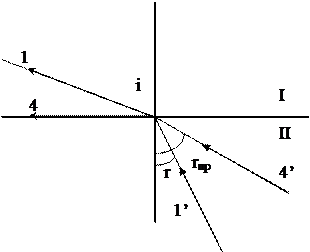
в обратном направлении вдоль луча 1. Если свет распространяется из среды с большим показателем преломления n₂ (оптически более плотной) в среду с меньшим показателем преломления n₁ (оптически менее плотную) (n₂> n₁), то согласно (1.4):

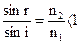(1.5)

Увеличивая угол r, увидим, что луч 1 приближается к поверхности SS. При некотором предельном луче r_ПР луч 1 совпадает с поверхностью SS. В этом случае 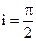. Соотношение (1.6) имеет вид:

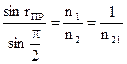
Следовательно, 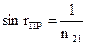. Для вакуума и воды r_ПР=48⁰,5.

При всех r> r_ПР луч не выйдет из среды 2 в среду 1, а отразится внутри среды 2. Поэтому при 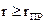наблюдается явление полного внутреннего отражения.

Явление полного внутреннего отражения используется в призмах полного отражения. Такие призмы применяются в оптических приборах (биноклях, перископах), а также в рефрактометрах.

Явление полного внутреннего отражения используется в световодах (светопроводах). Световоды используются в электролучевых трубках, ЭВМ, в медицине (диагностика желудка), для целей – оптики.

Электронная оптика.

Принцип Ферма. Оптико-механическая аналогия.

Принцип Ферма (или принцип наименьшего времени): действительный путь распространения света (траектория светового луча) есть путь, для прохождения которого свету требуется минимальное время по сравнению с любым другим мыслимым путем между теми же точками.

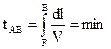(2.1)

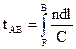(2.2)

Учитывая, что 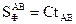-оптический путь луча в вакууме равен оптическому пути в среде с показателем преломления n.

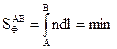(2.3)

Т.е. свет “выбирает” не только минимальное время. Но и минимальный оптический путь. Вся геометрическая оптика м.б. получена из принципа Ферма.

Принцип наименьшего действия (Мопертюи - Лагранжа)

Всякое тело движется по такой траектории, для которой интеграл:

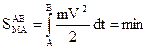, (2.4)

если его полная

Учитывая, что Vdt=de, m=const

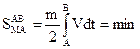(2.5)

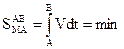(2.6)

Объединяя принцип Ферма и М-Л получаем выражение вида:

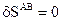(2.7)

где 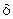-операция вариации величины действия S на пути АВ. Эта аналогия между оптическими и механическими экспериментальными принципами является следствие корпускулярно-волнового дуализма и носит наименование оптико-механической аналогии.

Электростатические и магнитные линзы.

Область физики и механики, в которых изучают вопросы формирования, фокусировки и отклонения пучков заряженных частиц и получения с их помощью изображений под действием электрического и магнитного полей в вакууме называется электронной оптикой.

Электростатические линзы–линзы в которых используют электрическое поле с выгнутыми и вогнутыми эквипотенциальными поверхностями.

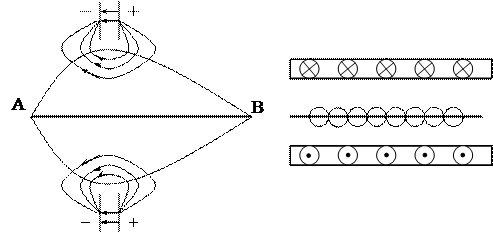Магнитная линза – линза . представляющая собой соленоид с сильным магнитным полем, коаксиальным пучку электронов.

Чтобы магнитное поле сконцентрировать на оси симметрии, соленоид помещают в железный кожух с узким внутренним кольцевым разрезом.

“Преломление” электрических и магнитных линз зависит от их фокусного расстояния. которые легко изменить манипуляцией полей 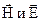. Как и в оптических системах, в электрооптических элементах также имеют место погрешности: сферическая аберрация, кома, дисторсия, астигматизм, ухудшающие разрешающую способность и качество изображения.