Понятие о колебательных процессах. Гармонические колебания.
Колебательные движения – одни из наиболее распространенных видов движения в природе и технике.
Колебательным движением мы будем называть такое движение, при котором параметры характеризующие движение с течением времени повторяются.
Существуют различные виды колебаний:
1. Свободные и вынужденные
2. Затухающие и незатухающие
3. Периодические и непериодические
Свободными называют колебания, происходящие только под действием внутренних сил колебательной системы.
Вынужденными называются колебания, происходящие под действием внешней периодической силы, действующей на колебательную систему.
Незатухающие колебания – колебания, в течении которых энергия колебательной системы не изменяется. В том случае, если энергия уменьшается колебания затухающие. В этом случае энергия превращается в другие ее виды, т.е. происходит ее диссипация ( рассеяние).
Периодические- такие колебания, для которых повторимость параметров происходит через строго постоянный промежуток времени – период. В противоположном случае колебания непереодические.
В зависимости от вида колебаний системы колебания могут быть механические, электрические, электромагнитные и т.д.
Если колебания свободны и незатухающие – собственные колебания.
Собственные периодические колебания получили название гармонических.
Гармонические колебания – простейший вид колебательного движения. На их примере мы изучаем основные закономерности этого движения.
1.2 Амплитуда, период, частота, круговая частота, фаза колебаний.
Гармонические колебания описываются при помощи так называемых гармонических законов: синуса и косинуса.
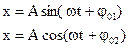 (1.1)
(1.1)
х – параметр, характеризующий отклонение системы от положения равновесия.
Пример:
А – амплитуда колебаний, максимальное отклонение системы от положения равновесия.
Периодом называется время, за которое система совершает одно полное колебание- Т.
Частота 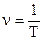 (1.2) показывает сколько колебаний совершает система в единицу времени (линейная частота).
(1.2) показывает сколько колебаний совершает система в единицу времени (линейная частота).
Существует понятие круговой и циклической частоты 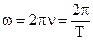 (1.3) показывающей, сколько колебаний совершает система за
(1.3) показывающей, сколько колебаний совершает система за 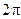 единиц времени.
единиц времени.
Фаза колебаний – величина, являющаяся аргументом синуса и косинуса.
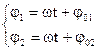 (1.4)
(1.4)
Значение фазы колебаний в начальный момент времени t=0 называется начальной фазой колебания. Это параметр, характеризующий состояние колебательной системы в начальный момент времени. Следует отметить, что начальная фаза может выбираться нами в какой-то степени произвольно в зависимости от того, какой гармонический закон взят нами для описания синус или косинус.
1.3 Скорость и ускорение гармонических колебаний. Основное уравнение динамики гармонических колебаний.
Для вычисления скорости и ускорения возьмем за основной закон синус:
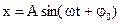 (1.5)
(1.5)
Мы будем рассматривать в данном случае механические колебания, но отметим, что все закономерности, полученные нами, будут справедливы и для колебаний другой природы.
Вычисляем скорость:
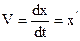 (1.6)
(1.6)
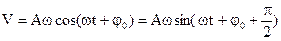 (1.7)
(1.7)
Формула (1.7) показывает, что 1) изменение скорости стечением времени тоже протекает по гармоническому закону. 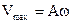 (1.8) 2) Изменение скорости со временем происходит со сдвигом фаз на
(1.8) 2) Изменение скорости со временем происходит со сдвигом фаз на 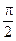 по отношению к изменению смещения со временем.
по отношению к изменению смещения со временем.
Находим ускорение, как производную скорости по времени.
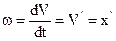 (1.9)
(1.9)
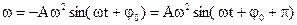 (1.10)
(1.10)
Формула (1.10) показывает, что изменение ускорения со временем также происходит по гармоническому закону. Максимальное значение ускорения вычисляется по формуле.
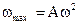 (1.11)
(1.11)
А – сдвиг фаз для ускорения.
Соотношение (1.10) можно записать также в виде
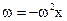 (1.12)
(1.12)
Если умножить левую и правую части (1.12) на массу, то получим: 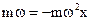 , а с учетом 2-го закона Ньютона:
, а с учетом 2-го закона Ньютона:
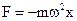 (1.13)
(1.13)
 (1.14)
(1.14)
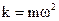 (1.15)
(1.15)
Формула (1.14) означает, что гармонические колебания происходят тогда, когда на колебания тела действует сила, линейно зависимая от смещения. Примером такой силы является сила упругости.
Если сила подчиняется соотношению (1.14), но не является упругой, то сила называется квазиупругой.
Гармонические колебания в механических системах происходят под действием либо упругих либо квазиупругих сил.
Перепишем соотношение (1.12) следующим образом
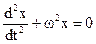 (1.16)
(1.16)
Уравнение (1.16) называется основным уравнением динамики гармонических колебаний. Оно является обыкновенным дифференциальным уравнением 2-го порядка. Решением его является гармонический закон синус или косинус.
1.4 Сложение колебаний одного направления, векторные диаграммы.
Гармонические колебания можно описывать при помощи следующего метода.
Представим себе, что в окружности точка О вращается радиус-вектор, длина которого равна амплитуде колебаний, а угловая скорость вращения совпадает с циклической частотой. Тогда проекции r на ось x и y будут находиться по формулам:
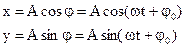
Такой способ описания колебаний называют методом векторных диаграмм. Его удобно применять в том случае, когда необходимо складывать колебания.
Рассмотрим случай, когда точка одновременно участвует в двух гармонических колебаниях, происходящих вдоль одного и того же направления. А нам надо найти результирующее колебание.
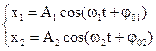 (1.17)
(1.17)
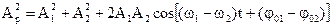 (1.18)
(1.18)
Если каждое из колебаний описывать данным методом, то амплитуду результирующего колебания можно найти в каждый момент времени как векторную сумму амплитуд исходных колебаний. Тогда по теореме косинусов амплитуда вычисляется по формуле (1.18).
Если частоты не равны, то, как следует из (1.18), амплитуда результирующего колебания будет зависеть от времени. В результате более сложное движение, чем гармонические колебания.
Рассмотрим простой случай, когда частоты совпадают 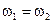 и кроме того разность фаз есть константа.
и кроме того разность фаз есть константа.
 (1.19)
(1.19)
Колебания, для которых выполняется условие (1.19) называются когерентными. При условии (1.19) соотношение (1.18) упрощается и принимает следующий вид:
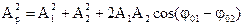 (1.20)
(1.20)
Результат, вычисляемый по формуле (1.20) полностью зависит от разности фаз.
Рассмотрим два частных случая:
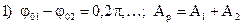 (1.21)
(1.21)
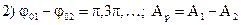 (1.22)
(1.22)
В первом случае колебания в результате сложения усиливают друг друга, а во втором ослабляют.
Так еслиА1=А2=А, то в случаях
1) Ар=2А 2) Ар=0
Такое явление называется интерференцией:
Это явление взаимного усиления или ослабевания когерентных колебаний в результате их сложения.
Определим начальную фазу колебания (рис. 2). Из рис. 2 видно, что
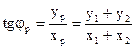 таким образом:
таким образом:
 (1.23)
(1.23)
1.5 Сложение взаимно перпендикулярных колебаний.
Возможны ситуации, когда точки одновременно участвуют в колебаниях происходящих во взаимно перпендикулярных направлениях. В этом случае результат сложения может быть гармоническое колебание или какое-либо другое, более сложное движение.
Рассмотрим:
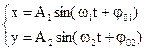 (1.24)
(1.24)
Сложить эти колебания означает найти уравнение результирующего колебания или если это не удается, то траекторию движения, в котором участвуют точки в результате сложения колебаний. Для иллюстрации рассмотрим два примера
1) 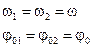
Разделим одно уравнение (1.24) на другое. В результате получим:
 (1.25)
(1.25)
(1.15) – уравнение траектории и прямой линии идущей следующим образом:
Траекторию движения точки вдоль прямой линии отклоняют от начала отсчета то в одну, то в другую сторону, причем отклонение z находится по теореме Пифагора: 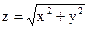 (1.26). Если в (1.26) подставить (1.24) получим:
(1.26). Если в (1.26) подставить (1.24) получим:
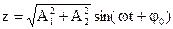 (1.27)
(1.27)
(1.27) – гармонический закон, только Ар находим по теореме Пифагора:
2) 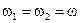
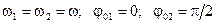
в этом случае уравнения имеют вид:
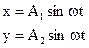
Выразим синус, косинус, возведем в квадрат и получим:
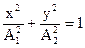 (1.28)
(1.28)
В этом случае уравнение (1.28) – уравнение эллипса, приведенного к главным осям.
ГЛАВА 2. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
2.1 Механические гармонические колебания, математический и физический маятники, пружинный маятник.
Математический маятник – материальная точка, подвешенная на невесомой и не растяжимой нити и колеблющаяся около положения равновесия.
Физический маятник – тело произвольной формы, подвешенное в точке, расположенной выше центра масс колеблющееся около положения равновесия.
Математический маятник – частный случай физического маятника, поэтому в начале рассмотрим колебания физического маятника и найдем частоту и период колебаний.
Точка О – точка подвеса, точка С – центр масс, 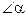 - угол отклонения от положения равновесия, d – плечо силы тяжести.
- угол отклонения от положения равновесия, d – плечо силы тяжести.
Колебания этого маятника можно рассмотреть как вращательное движение данного тела около центра вращения точки О, тогда для описания можно взять за основу основной закон динамики вращательного движения.
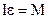 (2.1)
(2.1)
Моментом силы является момент силы тяжести.
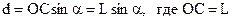 (2.2)
(2.2)
С учетом (2.2) формула для момента силы принимает следующий вид:
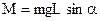 (2.3)
(2.3)
Подставляем (2.3) в (2.1) с учетом направления момента и получаем:
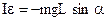 (2.4)
(2.4)
"-" говорит о том, что момент и угловое ускорение направлены в противоположные стороны.
Будем рассматривать малые отклонения для которых 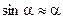 , тогда с учетом формулы для углового ускорения:
, тогда с учетом формулы для углового ускорения: 
получаем следующее соотношение:
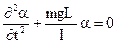 (2.5)
(2.5)
Уравнение (2.5) имеет вид основного уравнения динамики гармонических колебаний, частота которых находится по формуле:
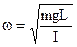 (2.6)
(2.6)
Тогда период колебаний найдется по формуле:
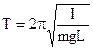 (2.7)
(2.7)
Точка О – точка в которой нить закреплена.
Обозначим длину математического маятника l=OC, тогда момент инерции колеблющейся точки относительно точки О будет равен:
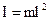 (2.8)
(2.8)
Если подставить (2.1) в (2.6) и (2.7) и учесть, что в данном случае l=L, то получим для циклической частоты и периода:
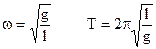 (2.9)
(2.9)
Если сравнить формулы (2.9) с формулами (2.6) и (2.7), то мы увидим, что для того чтобы эти формулы один и тот же вид необходимо, чтобы
 (2.10)
(2.10)
Эта величина называется приведенной длиной физического маятника. Она равна длине такого математического маятника период колебаний которого совпадает с периодом колебаний данного физического маятника.
Приводимая длина физического маятника меньше длины данного тела.
Рассмотрим пружинный маятник – тело некоторой массы m подвешенное на пружину. Предположим, что в положении равновесия сила тяжести, действующая на это тело уравновешено Fупр пружины, а когда мы отклоняем систему из положения, то движение происходит только под действием Fупр. Тогда 2-ой закон Ньютона имеет вид:
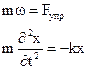 (2.11)
(2.11)
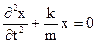 (2.12)
(2.12)
Уравнение (2.12) – уравнение гармонических колебаний, частота которых находится по формуле:
 (2.13)
(2.13)
а период колебаний:
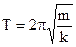 (2.14)
(2.14)
Рассмотрим, как ведет себя энергия колебательной системы в данных случаях. В случае гармонических колебаний скорость находится по формуле:
 , тогда
, тогда
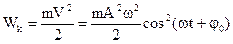 (2.15)
(2.15)
Потенциальная энергия в случае упругих или квазиупругих сил находится:
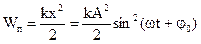 (2.16)
(2.16)
Если найти полную энергию
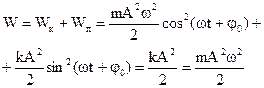 (2.17)
(2.17)
Формула (2.17) показывает, что полная энергия постоянна и действует закон сохранения энергии. Полная энергия колебаний равна максимальному значению кинетической или потенциальной энергии.
2.2 Электрические гармонические колебания в колебательном контуре.
Рассмотрим простую электрическую колебательную систему – колебательный контур.
L- катушка индуктивности, С- емкость конденсатора, R- сопротивление.
Запишем для этого закон Ома:
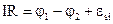 (2.18)
(2.18)
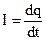 – сила тока (2.19)
– сила тока (2.19)
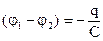 (2.20)
(2.20)
- разность зарядов на обкладках конденсатора.
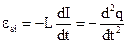 (2.21)
(2.21)
- ЭДС самоиндукции.
Если подставить (2.20) и (2.21) в (2.18) и выполнить некоторые преобразования, то имеем:
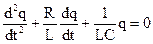 (2.22)
(2.22)
Наличие сопротивления в цепи приводит к рассеиванию энергии. Поэтому гармонические колебания будут тогда, когда сопротивление контура станет равным нулю, тогда уравнение (2.22) упрощается:
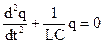 (2.23)
(2.23)
Уравнение (2.23) – уравнение гармонических колебаний, заряда q, причем частота колебаний находится:
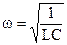 (2.24)
(2.24)
,а период колебаний:
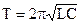 (2.25)
(2.25)
Формулы (2.24) и (2.25) – формулы Томпсона.
Колебательный контур в котором отсутствует сопротивление называется идеальным. С точки зрения энергии в этом контуре происходит превращение энергии катушки в энергию конденсатора и наоборот:
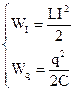 (2.26)
(2.26)
WI- энергия магнитного поля,
Wq- энергия электрического поля.
2.3 Свободные затухающие колебания. Логарифмический декремент затухания. Добротность
Рассмотрим затухающие колебания на примере механических и электрических колебаний. В случае механических колебаний они будут затухающими, если внутри системы существуют силы трения или силы сопротивления.
Мы рассмотрим тот случай, когда эти силы пропорциональны скорости.
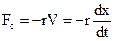 (2.27)
(2.27)
r- коэффициент сопротивления.
Тогда 2-ой закон Ньютона имеет следующий вид:
 (2.28) или:
(2.28) или:
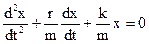 (2.29)
(2.29)
Введем обозначение: 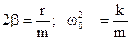 (2.30)
(2.30)
 - коэффициент затухания,
- коэффициент затухания,  - собственная частота колебаний. Теперь уравнение (2.29) имеет вид:
- собственная частота колебаний. Теперь уравнение (2.29) имеет вид:
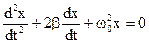 (2.31)
(2.31)
Уравнение (2.31) – основное уравнение динамики затухающих колебаний.
Решение этого уравнения можно записать следующим образом:
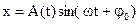 (2.32)
(2.32)
Где 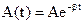 - затухает по этому закону (2.33)
- затухает по этому закону (2.33)
Частота затухающих колебаний не совпадает с собственной частотой колебаний, а находится по формуле:
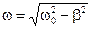 (2.24)
(2.24)
Возможен случай, когда  так велико, что
так велико, что 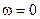 . Такие колебания называются ангармоническими. В этом случае затухающие колебания происходят за время равное периоду колебания. При небольших значениях колебания происходят более медленно, и график зависимости x от t имеет вид:
. Такие колебания называются ангармоническими. В этом случае затухающие колебания происходят за время равное периоду колебания. При небольших значениях колебания происходят более медленно, и график зависимости x от t имеет вид:
Уменьшается по экспоненциальному закону.
Натуральный логарифм двух последующих амплитуд различается на период Т называется логарифмическим декрементом затухания.
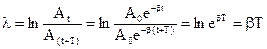
Пусть 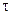 - время, за которое амплитуда уменьшится в е раз.
- время, за которое амплитуда уменьшится в е раз.

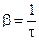

Где n – общее число колебаний
Добротность Q обратно пропорциональна логарифмическому декременту затухания.
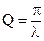
Рассмотрим электрические колебания. Вернемся к уравнению:
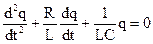
Обозначим в этом уравнении
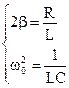 (2.35)
(2.35)
Тогда уравнение электрических колебаний принимает вид уравнения (2.31), т.е. основного уравнения затухающих колебаний.
Следовательно, и формулы (2.32), (2.33) и (2.34) будут справедливы для электрических колебаний. Единственно надо заменить смещение х зарядом q.
2.4 Вынужденные колебания механического осциллятора под действием синусоидальной силы. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые.
Рассмотрим случай, когда на колеблющееся тело действует внешняя периодическая сила. Будем считать, что эта сила изменяется по гармоническому закону.
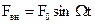 (2.36)
(2.36)
Запишем 2-ой закон Ньютона:
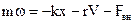 (2.37)
(2.37)
После всех преобразований получим формулу:
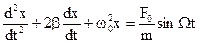 (2.38)
(2.38)
Уравнение (2.38) – основное уравнение динамики вынужденных колебаний.
С точки зрения теории дифференциальных уравнений это неоднородное уравнение потому его решение складывается их двух слагаемых:
1) Общее решение соответствующего однородного уравнения, т.е. уравнения затухающих колебаний.
2) Частного решения данного неоднородного уравнения.
Можно записать:
 (2.39)
(2.39)
В этом случае говорят, что вынужденные колебания не установились, а наблюдается так называемый переходный режим. С течением времени первое слагаемое в (2.39) стремится к нулю, так как это оно описывает затухающие колебания, и, начиная с некоторого момента времени, можно записать что
x=x2(t), где х2 – частное решение неоднородного уравнения (2.38)
Такие колебания называются установившимися вынужденными колебаниями. И это частное решение имеет вид:
 (2.40)
(2.40)
где Авын находится по формуле:
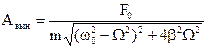 (2.41)
(2.41)
Начальная фаза находится из соотношения:
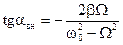 (2.42)
(2.42)
Из формулы видно, что амплитуда вынужденных колебаний может принимать разные значения, в зависимости от соотношения частоты колебаний и частоты вынуждающей силы. Поэтому соотношение (2.41) можно исследовать на максимум. Ясно, что это соотношение будет достигать максимального значения тогда, когда подкоренное выражение
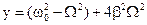 (2.43)
(2.43)
достигнет минимального значения. Находим производную, y=0.
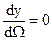
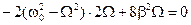
После сокращения 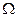 и приведения подобных членов получаем:
и приведения подобных членов получаем:
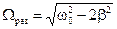 (2.44)
(2.44)
где 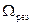 - резонансная частота. При этом если частота вынуждающей силы совпадает с резонансной частотой, то наблюдается резкое возрастание амплитуды вынужденных колебаний – резонанс.
- резонансная частота. При этом если частота вынуждающей силы совпадает с резонансной частотой, то наблюдается резкое возрастание амплитуды вынужденных колебаний – резонанс.
Из формулы (2.44) видно, что в случае незатухающих колебаний , когда резонансная частота совпадает с собственной частотой:
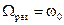 (2.45)
(2.45)
График зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной кривой (РК). РК имеет ярко выраженный максимум в точке 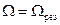 .
.
Острота пика (максимума) зависит от коэффициента затухания. Эту зависимость можно получить аналитически. Если в формулу для амплитуды вынужденных колебаний (2.41) подставить значение резонансной частоты (2.44). В результате получится формула:
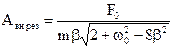 (2.46)
(2.46)
Из формулы (2.46) видно при 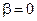 правая часть обращается в бесконечность. Таким образом РК будут иметь следующий вид:
правая часть обращается в бесконечность. Таким образом РК будут иметь следующий вид:
По мере увеличения  максимум РК будет передвигаться к началу координат и сама РК является все более и более пологой. При
максимум РК будет передвигаться к началу координат и сама РК является все более и более пологой. При 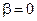 максимум РК равен бесконечности и приходится строго на собственную частоту колебаний.
максимум РК равен бесконечности и приходится строго на собственную частоту колебаний.
2.5 Осциллятор, как спектральный прибор. Фурье – разложение. Физический смысл спектрального разложения.
В природе и технических достижениях часто встречаются более сложные виды колебаний, чем гармонические колебания. Их изучение представляет собой трудную задачу, для облегчения которой существует метод сведения одного сложного колебания к множеству простых колебаний. Одним из таких методов является разложение сложного колебания в бесконечный ряд, членами которого являются гармонические функции, содержащие кратные частоты. Такое разложение называется Фурье-разложением и соответствует ряду Фурье.
Предположим, что сложное колебание описывается некоторой произвольной функцией S(t)=f(t) ,тогда разложение этой функции в ряд Фурье будет иметь следующий вид:
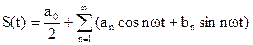 (2.47)
(2.47)
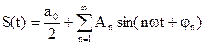 (2.48)
(2.48)
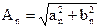 (2.49)
(2.49)
где частоты 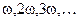 называются гармониками.
называются гармониками.  - основная или 1-ая гармоника. Остальные называют дополнительными гармониками.
- основная или 1-ая гармоника. Остальные называют дополнительными гармониками.
Коэффициенты an и bn называют коэффициентами ряда Фурье и они вычисляются по формулам Эйлера – Фурье:
 (2.50)
(2.50)
Периодические колебания имеют дискретный ряд Фурье. А непериодические колебания имеют непрерывный ряд Фурье.
Совокупность частот, по которым происходит разложение данного колебания, называется не совокупностью частот, а совокупностью самих колебаний, на которые происходит разложение. В зависимости от того, как распределены гармоники, спектры могут быть линейчатыми (в случае дискретного распределения гармоники) или сплошными (в случае непрерывного распределения гармоник).
Разложением сложных колебаний в ряд Фурье позволяет в большинстве случаев заменить изучение этого колебания изучением нескольких достаточно простых колебаний. Это происходит в том случае, когда коэффициенты ряда Фурье являются убывающими и следовательно сам ряд можно оборвать при некотором конкретном значении (n не равно бесконечности). В этом заключается физический смысл спектрального разложения.
2.6 Модулированные колебания. Спектр амплитудно-модулированного колебания.
Если какой-либо из параметров колебаний меняется с течением времени по определенному заданному закону, то говорят о модуляции колебаний. Колебания в этом случае называются модулированными. Наиболее широко распространены два вида модуляции:
1) Модуляция амплитудная,
2) Модуляция частотная.
В 1-ом случае с течением времени изменяется амплитуда колебаний, во 2-ом – частота.
Изменение этих параметров должно происходить медленнее, чем сами колебания. Это означает, что время изменения параметров в должно быть меньше чем период колебаний.
Рассмотрим более подробно амплитудное модулированное колебание, если немодулированное колебание зависит негармоническим законом.
 (2.51)
(2.51)
то соответствующие модулированные колебания для случая амплитудной модуляции будет описываться законами следующего вида:
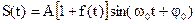 (2.52)
(2.52)
Здесь функция несет в себе основную информацию об ограничении амплитуды. На нее накладываются ограничения:
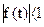 (2.53)
(2.53)
Наиболее часто встречаются случаи, когда функция сама является периодической. В этом случае частота ее изменения должна быть гораздо меньше, чем частота самого колебания.
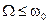 (2.54)
(2.54)
Модулированное колебание можно разложить в спектральный ряд. Покажем это на примере, когда функция является гармонической:
 (2.55)
(2.55)
Если подставить (2.55) в (2.52), то получим следующую формулу:
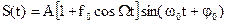 (2.56)
(2.56)
Такое колебание можно разложить в спектральный ряд, состоящий из трех слагаемых, частоты которых принимают значения 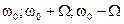 . Непосредственной подстановкой можно убедиться, что соответствующее разложение имеет вид:
. Непосредственной подстановкой можно убедиться, что соответствующее разложение имеет вид:
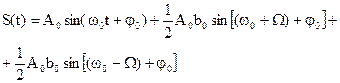 (2.57)
(2.57)
Таким образом, амплитудно-модулированное колебание разлагается в спектр, состоящий из трех колебаний.
2.7 Нелинейный осциллятор. Физические системы, содержащие нелинейность.
Если колебания описываются линейными дифференциальными уравнениями, то они называются линейными колебаниями.
В противоположном случае колебания называются нелинейными.
Общий вид нелинейного дифференциального уравнения, описывающего колебания следующий:
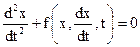
Если функция f имеет вид 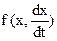 (2.58), то колебания называются автономными.
(2.58), то колебания называются автономными.
Если эта функция имеет вид f=f(x) (2.59), то колебания называются консервативными.
Мы до сих пор рассматривали случай, когда функция f(x) была линейной. В механике эта функция соответствует возвращающей силе, приведенной к единице массы. Таким образом, механические колебательные системы будут нелинейными в том случае, когда возвращающая сила зависит от смещения х нелинейно.
Для электрических колебаний роль х выполняет заряд и в простейшем случае (линейном) функция f(q) подчиняется линейному соотношению, аналогично закону Гука в механике.
В более сложных случаях в электрических колебательных системах могут возникать нелинейности связей, с наличием в системе либо обратных связей, либо зависимости от временных параметров, характеризуют всю систему (индуктивность L, емкость С).
Для ангармонических колебаний характером связи является зависимость периода колебаний от амплитуды колебаний. В общем случае эту зависимость можно описать следующей формулой:
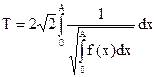 (2.60)
(2.60)
Из этой формулы видно, что конкретный вид определен видом функции f(x).
Например:
1) f(x)=x3 (2.61)
Подставим (2.61) в (2.60) и проинтегрируем:
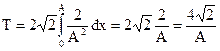 (2.62)
(2.62)
2) Нелинейными являются колебания математического маятника в том случае, когда он отклоняется от положения равновесия на угол больше 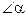 . В этом случае уравнение колебаний имеет следующий вид:
. В этом случае уравнение колебаний имеет следующий вид:
 (2.63)
(2.63)
Таким образом, функция 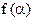 имеет вид:
имеет вид:
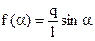 (2.64)
(2.64)
Если подставить (2.64) в (2.60), то получим зависимость периода колебаний от угла отклонения маятника от положения равновесия:
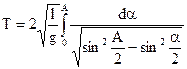 (2.65)
(2.65)
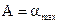 - максимальное значение угла отклонения от положения равновесия.
- максимальное значение угла отклонения от положения равновесия.
Зависимость (2.65) в явном виде не интегрируется.
Интеграл называется эллиптическим. Но зависимость можно разложить в степенной ряд.
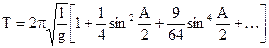 (2.66)
(2.66)
Из формулы (2.66) видно, что обычная формула математического маятника получается из случая, когда под рядом в квадратных скобках остается только первое слагаемое.
ГЛАВА 3. ВОЛНОВЫЕ ПРОЦЕССЫ
3.1 Волны. Уравнение волны и волновое уравнение. Плоская и сферическая синусоидальные волны. Амплитуда, частота, фаза и длина волны, волновое число. Фазовая скорость.
Рассмотрим колебания не материальной точки, а некоторой частицы среды, связанной с другими частицами тем или иным взаимодействием. В этом случае колебание данной частицы будет вызывать (благодаря взаимодействию) колебания соседних с ней частиц. То есть в процесс колебаний будут вовлекаться все новые и новые частицы среды и колебания будут распространятся в данной среде – волновой процесс, а сами колебания, распространяющиеся в среде - волны.
Если взаимодействия между частицами среды упругие, то такая среда называется упругой, и волны, в которой они распространяются тоже упругие.
Обычно, для волны является характерно то, что происходит процесс переноса энергии от точки к точке данной среды без переноса вещества – волна бегущая. Кроме бегущей существуют стоячие волны, для которых является характерным отсутствие переноса энергии.
Линия, вдоль которой происходит перенос энергии, называется лучом.
По касательной к этой линии, в общем случае, направлена скорость.
1. Продольные упругие волны, когда частицы среды колеблются в направлениях скорости распространения волны.
2. Поперечные волны, в этом случае частицы среды колеблются в направлениях перпендикулярных скорости распространения волны.
Существует особый вид волн, которые возникают на поверхности жидкости. Они называются поверхностными волнами. Для них характерно то, что частицы жидкости в процессе колебаний движутся по сложным траекториям. И это движение происходит одновременно и вдоль скорости, и перпендикулярно скорости.
Поперечные и продольные, упругие волны могут возникать в тех или иных веществах в зависимости от упругих свойств этих веществ. Так если вещество отличается упругостью по отношению к изменению объема, в таком веществе возникают только продольные волны.
Если вещество отличается упругостью по отношению к изменению формы, то в нем могут возникать поперечные волны.
В случае поперечных волн частицы среды колеблются в плоскости перпендикулярной скорости распространения волны, причем в общем случае направление этих колебаний может в течение времени меняться, хаотично оставаясь на этой плоскости. Такая волна называется естественной (неполяризованной). Если каким-то образом упорядочить направление колебаний, то волна становится поляризованной, а само явление упорядочения направления колебаний называется поляризацией.
Если ввести на плоскости, в которой происходит колебание частицу среды, оси X Y, то результирующее колебание можно представить как сумму двух взаимно перпендикулярных. В этом случае траектория движения частицы, в зависимости от разности фаз складываемых колебаний, может быть:
1) Прямой линией (поляризация называется линейной).
2) Эллипсом или окружностью (поляризация называется эллиптической или круговой).
Процесс распространения колебаний можно описать математически при помощи уравнения, которое связывает параметр, характеризующий отклонение точек среды от положения равновесия с пространственными и временными координатами.
Если обозначить параметр буквой S-смещение от положения равновесия, то уравнение волны:
S=f(x, y, z, t)
Если колебания точек среды происходит по гармоническому закону, то волна называется синусоидальной или гармонической.
Геометрическое место точек среды колебаний в одинаковых фазах называют волновой поверхностью или фронтом волны.
Если волновые поверхности представляют собой плоскости параллельные друг другу, то волна называется плоской.
Плоская синусоидальная волна – простой вид волны. Волна распространяется вдоль только одного направления. Луч представляет собой прямую линию, которая обычно совпадает с осью X. Уравнение волны упрощается:
S = f(x, t)
Выведем уравнение для плоской синусоидальной волны:
Колебания в каждой точке описываемые при помощи обычного гармонического закона, по колебаниям в точке отстающей от данной точки на расстояние X будут запаздывать на время 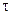 =x/v, которое необходимо волне, чтобы распространится от одной точки к другой. Таким образом колебания в произвольной точке будут описываться в общем случае соотношением:
=x/v, которое необходимо волне, чтобы распространится от одной точки к другой. Таким образом колебания в произвольной точке будут описываться в общем случае соотношением:
S=S(t')=S(t-τ)=S(t- 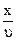 ) (3.2)
) (3.2)
Если вместо s подставить гармонический закон:
S=A sin (ωt '+ φo)=A sin [ω (t- 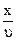 )+φo]=A sin (ωt-
)+φo]=A sin (ωt- 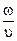 x+φo). (3.3)
x+φo). (3.3)
Уравнение (3.3) – уравнение плоской синусоидальной волны.
Если волновые поверхности являются концентрическими сферами или поверхностями, то волна называется сферической.
Она описывается аналогичным уравнением в котором роль X выполняет расстояние от центра сферических поверхностей, где располагается источник волны, до данной точки.
S=A(r) sin(ωt- 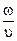 r+φo) (3.4)
r+φo) (3.4)
Вторым отличием сферической волны является то, что амплитуда колебаний зависит от расстояния r .
A(r)=  (3.5)
(3.5)
Точно также как колебания можно было описать с помощью дифференциальных уравнений (основных уравнений динамики) волновой процесс можно описать с помощью дифференциального уравнения, которое называется волновым уравнением.
Это уравнение относительно параметра S , так как этот параметр зависит от двух переменных, то это уравнение является дифференциальным уравнением частных производных.
Для плоской синусоидальной волны уравнение имеет вид:
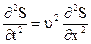 (3.6)
(3.6)
(3.6) – простейшее волновое уравнение.
В общем виде, оно имеет вид:
 (3.7)
(3.7)
где 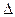 , так как оператор Лапласа
, так как оператор Лапласа
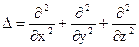
Сферическая синусоидальная волна описывается уравнением (3.7), в котором оператор Лапласа описывается в сферических координатах.
Рассмотрим уравнение волны и параметры в него входящие:
S=A sin ( 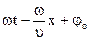 )
)
А – амплитуда колебаний частиц среды, которая одновременно является и амплитудой волны.
ω - циклическая частота колебаний среды, циклическая частота волны.
υ, Т – частота и период колебаний, частота и период волны.
Выражение являющееся аргументом синуса называется фазой волны.
Φ= 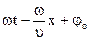 (3.10)
(3.10)
Фаза волны отличается от фазы колебаний, так как зависит от двух параметров X и Z. Каждая волна характеризуется длиной.
Длина волны – расстояние, которое проходит волна за время равное периоду колебаний.
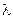 =
= 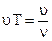 =
= 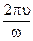 (3.11)
(3.11)
Длиной волны называют кратчайшее расстояние между двумя точками волны, колеблющимися в одинаковых фазах.
С учетом (3.11) отношение 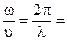 k (3.12)
k (3.12)
Где k – волновое число, которое показывает сколько раз длина волны укладывается на 2 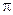 единицы длины.
единицы длины.
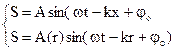 (3.13)
(3.13)
Скорость с которой распространяются волновые поверхности называется фазовой скоростью.
Формулу для нее можно получить, если продифференцировать по времени соотношение (3.14).
 t-kx+
t-kx+ 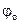 =const
=const
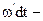 k dx=0
k dx=0
v= 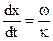 (3.15)
(3.15)
3.2 Принцип суперпозиции волн. Групповая скорость и ее связь с фазовой скоростью, распространение волн в средах с дисперсией.
Если колебания точек среды описываются линейными уравнениями, то такая среда называется линейной. Для линейных сред справедлив принцип суперпозиций волн. Согласно которому, если в данной среде распространяются одновременно несколько волн, то каждая точка среды участвует в колебаниях принадлежащих каждой волне независимо от колебаний принадлежащим другим волнам, поэтому результирующее колебание описывают параметрами, которые находят как суммы параметров исходных колебаний.
Это такие параметры: смещение-S, скорость-V, ускорение-  .Таким образом принцип суперпозиции можно записать математически в виде 3-х соотношений.
.Таким образом принцип суперпозиции можно записать математически в виде 3-х соотношений.
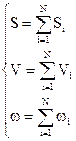 (3.18)
(3.18)
При помощи принципа суперпозиции можно представлять синусоидальные волны в виде некоторого числа синусоидальных волн.
Рассмотрим такое представление на примере квазисинусоидальной волны. Такая волна получается при сложении 2-х синусоидальных волн одинаковой амплитуды и очень близких частот.
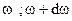
k ; k+dk
S=A sin ( 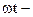 kx)+A sin [(
kx)+A sin [( 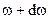 )t-(k+dk)x]=2Acos
)t-(k+dk)x]=2Acos 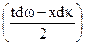 ·sin(
·sin( 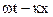 ) (3.19)
) (3.19)
Соотношение (3.19) можно переписать в виде:
S=Aг sin( 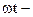 kx) (3.20)
kx) (3.20)
Aг=2A cos 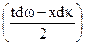 (3.21)
(3.21)
Совокупность волн из которых складывается произвольная несинусоидальная волна называется спектром волны. Также спектром называют совокупность частот этих волн.
Группа волн называется волновым пакетом и скорость с которой она распространяется отличается от фазовой скорости. Эта скорость называется групповой скоростью. Ее можно определить следующим образом: зафиксировать точку волнового пакета, которой соответствует постоянное значение амплитуды Аг и установить скорость движения этой точки. Это и будет групповая скорость.
Aг=const
td  -xdk=const (3.22)
-xdk=const (3.22)
u= 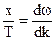 (3.23)
(3.23)
u-групповая скорость.
Групповая скорость- скорость переноса энергии волновым пакетом, в этом заключается его физический смысл.
Установим связь между групповой скоростью и фазовой:
 (3.24)
(3.24)
Подставим (4.24) в (3.23)
u= 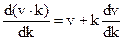 (3.25)
(3.25)
Если учесть, что 
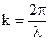 (3.26)
(3.26)
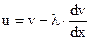 (3.27)
(3.27)
Существуют среды, в которых фазовая скорость волны зависит от длины волны или частоты. Такие среды называются диспергирующими. А само явление зависимости называется дисперсией волн. Если волновой пакет распространяется в такой среде, то волны его составляют движение с различными фазовыми скоростями и в результате волновой пакет меняет свою форму-"расплывается".
3.3 Интерференция монохроматических волн. Временная и пространственная когерентность. Интерференция синусоидальных волн. Стоячие волны.
Рассмотрим две синусоидальные волны, каждая из которых имеет свою собственную амплитуду, частоту и начальную фазу. Кроме того будем рассматривать такой случай, когда источники этих волн находятся на различных расстояниях r1 и r2 до той точки, в которой происходит сложение колебаний.
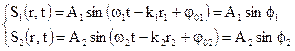 (3.28)
(3.28)
Если применить для сложения колебаний точек среды, которые они испытывают благодаря наличию этих двух волн, метод векторных диаграмм, то для амплитуды результирующего колебания можно записать следующую формулу:
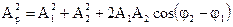 (3.29)
(3.29)
А для разности фаз:
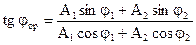 (3.30)
(3.30)
Из формулы (4.29) видно, что амплитуда результирующего колебания зависит от разности фаз:
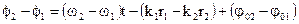 (3.31)
(3.31)
В общем случае эта разность фаз зависит от времени и результирующая амплитуда будет функцией t. Если разность частот:( 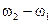 ) достаточно велико, то изменение результирующей амплитуды будет происходить так быстро, что зарегистрировать прибором можно будет только среднее значение амплитуды, взятое за достаточно продолжительный промежуток времени τ.
) достаточно велико, то изменение результирующей амплитуды будет происходить так быстро, что зарегистрировать прибором можно будет только среднее значение амплитуды, взятое за достаточно продолжительный промежуток времени τ.
Вычислим среднее значение квадрата результирующей амплитуды:

За знак интеграла можно вынести те величины, которые не зависят от времени:
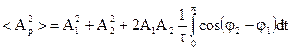 (3.32)
(3.32)
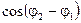 за время τ>>T изменяется от +1 до –1, поэтому интеграл, выражающий его среднее значение, обращается в ноль. Следовательно, получаем:
за время τ>>T изменяется от +1 до –1, поэтому интеграл, выражающий его среднее значение, обращается в ноль. Следовательно, получаем:
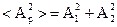 (3.33)
(3.33)
Вычислим результирующую амплитуду в том случае, когда колебания точек среды являются когерентными. В этом случае 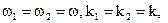 поэтому
поэтому 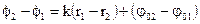 (3.34)
(3.34)
Введем 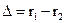 (3.35) и перепишем (3.34) с учетом (3.35)
(3.35) и перепишем (3.34) с учетом (3.35)
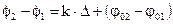 (3.36)
(3.36)
Если подставить (3.36) в (3.29), то мы увидим, что возможны ситуации, когда результирующая амплитуда будет максимальной или минимальной.
В общем случае разность фаз должна иметь следующее значение:
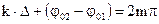 (3.37)
(3.37)
Во втором случае: 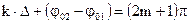 (3.38)
(3.38)
Где m-любое целое число.
Условия (3.37) и (3.38) можно преобразовать для геометрической разности хода.
1-е условие дает:
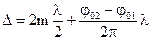
2-е условие дает:
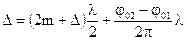
Объединив эти два условия в одно, получим (3.39).
Наиболее интересным является тот случай, когда начальные фазы колебания совпадают.
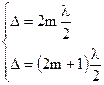 (3.40)
(3.40)
То есть все определяется геометрической разностью хода складываемых волн, при этом, если выполняется условие максимума, то для результирующей амплитуды:
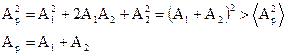
В случае минимума:
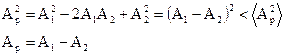
При сложении когерентных волн мы получаем устойчивую во времени пространственную картину, в которой наблюдаются максимумы и минимумы в различных точках пространства. Такое явление называется явлением интерференции. Картина называется интерференционной картиной, а условия максимума и минимума называются условиями интерференционных максимумов и минимумов.
Стоячие волны – частный случай интерференции, когда складывают волны, которые имеют одинаковую амплитуду и распространяются на встречу друг другу, вдоль некоторого направления. Пусть это направление будет направлением оси Х, тогда уравнение складываемых волн будет иметь вид:
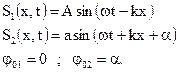
Первая волна распространяется в сторону положительного направления оси Х, а вторая волна ей на встречу, поэтому мы получаем разные знаки перед пространственной частью фаз этих волн.
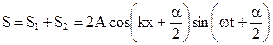 (3.41)
(3.41)
Таким образом, уравнение результирующей волны разбивается на два сомножителя. Один из которых зависит только от пространственных координат, а второй только от временных это позволяет переписать уравнение следующим образом:
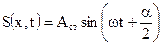 (3.42)
(3.42)
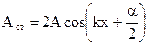 (3.43)
(3.43)
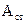 -амплитуда стоячей волны.
-амплитуда стоячей волны.
Как видно из уравнения (3.43) амплитуда меняется по гармоническому закону.
Там где наблюдается максимум амплитуды, находятся так называемые кучности стоячей волны. Там где наблюдаются минимумы, находятся узлы стоячей волны.
Их положения можно найти, используя условия максимума для правой части (3.43).
 (3.44)
(3.44)
где 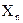 -координаты кучности.
-координаты кучности.
 -координаты узла.
-координаты узла.
Длиной стоячей волны называют расстояние между соседними кучностями или соседними узлами.
3.4 Энергия волны. Вектор Умова.
При распространении упругих волн каждая точка среды участвует в упругих колебаниях, поэтому имеет как кинетическую, так и потенциальную энергию. Полная энергия точки в каждый момент времени t равна суммарной кинетической и суммарной потенциальной. По мере распространения волны происходит перенос энергии от одной точки среды к другой. Введем плотности энергии:
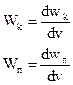 (3.45)
(3.45)
Можно показать, что первая величина выражается следующей формулой:
 (3.46)
(3.46)
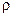 -плотность данной среды, v1-скорость, которую имеют точки среды благодаря участию в колебании. Мы предполагаем, что эта скорость одна и та же для всех точек среды находящихся в объеме dv.
-плотность данной среды, v1-скорость, которую имеют точки среды благодаря участию в колебании. Мы предполагаем, что эта скорость одна и та же для всех точек среды находящихся в объеме dv.
Аналогично для плотности потенциальной энергии существует формула:
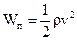 ε2 (3.47)
ε2 (3.47)
v-фазовая скорость волны, ε - относительная деформация среды.
Между скоростью V и V1 существует связь, которая выражается следующей формулой:
V1=V ε (3.48)
Отсюда видно, что:
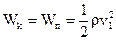 (3.49)
(3.49)
Следовательно, плотность полной энергии:
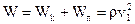 (3.50)
(3.50)
Если волна гармоническая, то выражение плотности полной энергии имеет вид:
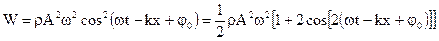 (3.51)
(3.51)
При помощи формулы (4.51) удобно находить среднее значение плотности полной энергии. Если усреднять за время большее чем период колебаний, то среднее значение от косинуса будет равно нулю, и мы получим:
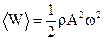 (3.52)
(3.52)
То есть среднее значение полной энергии равно половине от максимального значения. Выведем понятие потока энергии как величину численно равную энергии, которая переносится через некоторую площадку в единицу времени перпендикулярно этой площадке.
Общая формула для этой величины имеет вид:
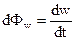 (3.53)
(3.53)
Рассмотрим площадку dS, ориентированную под некоторым углом α по отношению к направлению распространения волны и найдем, какая энергия будет переноситься волной через эту площадку. Для этого вычислим W заключенную в заштрихованном объеме.
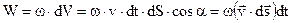 (3.54)
(3.54)
Подставим (3.54) в (3.53):
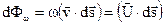 (3.55)
(3.55)
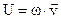 (3.56)
(3.56)
 -вектор плотности потока энергии (Умова).
-вектор плотности потока энергии (Умова).
Используя вектор Умова можно находить конечный поток энергии:
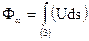 (3.57)
(3.57)
Можно ввести понятие интенсивности волны. Это величина равна модулю среднего значения вектора Умова.
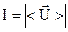 (3.58)
(3.58)
ГЛАВА 4. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ИХ СВОЙСТВА
4.1 Скорость распространения электромагнитных возмущений. Волновое уравнение для электромагнитных волн. Свойства электромагнитных волн. Электромагнитная природа световых волн.
Электромагнитными волнами называют совокупность переменных электрического и магнитного полей распространяющихся в пространстве.
Очень важная особенность электромагнитных волн заключается в том, что для их распространения не нужна какая либо среда. Более того, с максимальной скоростью и без потерь энергии, лучше всего электромагнитные волны распространяются в вакууме. Эта особенность электромагнитных волн долгое время воспринималась ученными как нечто невероятное, поэтому много сил было потрачено на поиски такой среды возмущения, которая представляла бы собой электромагнитные волны (теория эфира).
Запишем первые два уравнения Максвелла:
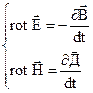 (4.59)
(4.59)
Используем связь между векторами:
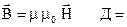 ε
ε 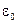
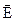 (4.60)
(4.60)
Кроме того, рассмотрим простейший случай, когда вектора 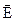 и
и 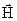 зависят только лишь от одной переменной пространственной координаты от Х, то есть одномерный случай, тогда:
зависят только лишь от одной переменной пространственной координаты от Х, то есть одномерный случай, тогда:
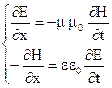 (4.61)
(4.61)
Первое уравнение из этой системы дифференцируем по Х, второе по t.
 (4.62)
(4.62)
Исключаем смешанные производные:
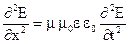 (4.63)
(4.63)
В этом уравнении связаны вторые производные. Оно имеет вид волнового уравнения для вектора 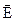 .
.
Для того чтобы это уравнение совпадало с волновым необходимо ввести обозначения.
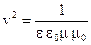 ;
; 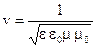 (4.64)
(4.64)
Если продифференцировать первое уравнение (4.61) по t, а второе по Х, то в результате точно таких же преобразований получим такое же уравнение вида (4.63) для вектора 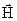 :
:
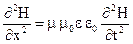 (4.65)
(4.65)
В выражение для v (4.64) входят две постоянные: 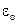 и
и 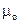 , выведем новую постоянную:
, выведем новую постоянную:
 (4.66)
(4.66)
С- электродинамическая постоянная.
Таким образом, мы получили волновые уравнения для векторов напряженностей электрического и магнитного полей. Это означает, что мы доказали существование электромагнитных волн, механизм распространения которых, состоит в следующем:
Переменное во времени электрическое поле благодаря тому, что оно представляет собой вихревой электрический ток, порождает переменное во времени магнитное поле, которое при помощи явления электромагнитной индукции порождает переменное во времени электрическое поле и так далее.
Скорость распространения электромагнитной волны может быть записана в форме:
 (4.67)
(4.67)
Если волна распространяется в вакууме, то 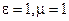 , тогда V=C (4.68)
, тогда V=C (4.68)
Если в формулу (4.66) подставить численные значения 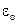 и
и 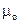 , то в результате вычислений мы получим:
, то в результате вычислений мы получим:
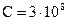 м/с
м/с
Известно, что именно такое значение имеет скорость распространения света в вакууме. Из этого совпадения Максвелл вывел предположение о том, что световые волны являются по своей природе именно электромагнитными волнами. Дальнейшее изучение электромагнитных волн доказало справедливость предположения Максвелла.
Электромагнитные волны обладают следующими свойствами:
1). Возможность распространения в вакууме.
2). Можно доказать, что вектора 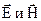 в электромагнитном поле взаимно перпендикулярны и перпендикулярны вектору
в электромагнитном поле взаимно перпендикулярны и перпендикулярны вектору 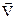 (скорости волны), причем
(скорости волны), причем
