Временная и пространственная когерентность

Интерференция световых волн. Способы наблюдения интерференции света. Расчет интерференционной картины для щелей Юнга

Временная и пространственная когерентность

Когерентностью называется согласованное протекание. нескольких колебательных или волновых процессов, Степени согласованности может быть различной. Соответственно можно ввести понятие степени когерентности двух волн.

Различают временную и пространственную когерентность, Мы начнем с рассмотрения временной когерентности.

Временная когерентность. Описанный в предыдущем параграфе процесс интерференции является идеализированным. В действительности этот процесс гораздо более сложен. Это обусловлено тем, что монохроматическая волна, описываемая выражением

Acos(wt – kr + a),

где A,w и a— константы, представляют собой абстракцию. Всякая реальная световая волна образуется наложением колебаний всевозможных частот (или длин волн), заключенных в более или менее узком, но конечном интервале частот Dw (соответственно длин волн Dl). Даже для света, который считается монохроматическим (одноцветным), интервал частот Dw является конечным. Кроме того, амплитуда волны A и фаза a претерпевают со временем непрерывные случайные (хаотические) изменения. Поэтому колебания, возбуждаемые в некоторой точке пространства двумя накладывающимися друг на друга световыми волнами, имеют вид

A₁(t)cos[w₁(t) t+a₁(t)], A₂(t)cos[w₂(t) t+a₂(t)].

(1)

причем хаотические изменения функций A₁(t), A₂(t),w₁(t), w₂(t), a₁(t), a₂(t), являются совершенно независимыми.

Для простоты будем считать амплитуды A₁ и A₂ постоянными. Изменения частоты и фазы можно свести либо «"изменению одной лишь фазы, либо к изменению одной лишь частоты. Представим функцию

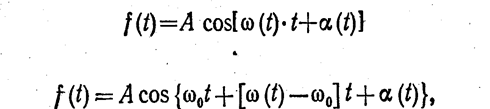
где w₀— некоторое среднее, значение частоты, и введем обозначение w[(t) - w₀]t+a(t)=a¢(t). Тогда формула (2) примет вид

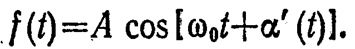
(3)

Мы получили функцию, у которой хаотические изменения претерпевает лишь фаза колебания.

С другой стороны, в математике доказывается, что негармоническую функцию, например функцию (2), можно представить в виде суммы гармонических функций с частотами, заключенными в некотором интервале Dw

Таким образом, при рассмотрении вопроса о когерентности возможны два подхода: «фаэовый» и «частотный», Начнем с «фазового» подхода. Допустим, что частоты w₁ и w₂ в формулах (1) удовлетворяют условию,w₁=w₂=const, и выясним какое влияние, оказывает изменение фаз a₁ и a₂. В соответствии с формулой (2) при сделанных предположениях интенсивность света в данной точке определяется выражением

где d(t)=a₂(t)—a₁(t). Последнее слагаемое в этой формуле носит название интерференционного члена.

Всякий прибор, с помощью которого можно наблюдать интерференционную картину (глаз), фотопластинка и т.п., обладает некоторой инерционностью. В cвязи с этим он регистрирует картину, усредненную по промежутку времени t_приб, необходимому для «срабатывания» прибора. Если за время t_приб, множитель cos d (t) принимает все значения от—1 до +1, среднее значение интерференционного члена будет равно нулю. Поэтому регистрируемая прибором интенсивность окажется равной сумме интенсивноcтей, создаваемых в данной точке каждой из волн в отдельности,— интерферен­ция отсутствует, и мы вынуждены признать волны некогерентными,

Если же за время t_приб, значение cos d(t) остается практически неизменным, прибор обнаружит интерференцию, и волны надо признать когерентными.

Из сказанного следует, что понятие когерентности является относительным: две волны могут вести себя как когерентные при наблюдении с одним прибором (с малой инерционностью) и какнекогерентные при наблюдении с другим прибором (с большей инерционностью). Для характеристики когерентных свойств волн вводится время когерентности t_ког , которое определяется как такое время за которое случайное изменение фазы волны a(t) достигает значения порядка p. За время t_ког колёбаниё как бы забываёт свою первоначальную фазу и становится некогерентным по отношению к самому себе.