Задачи очень трудные. D1.Пластины плоского конденсатора соединены ди­электрической пружиной (рис

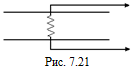
D1.Пластины плоского конденсатора соединены ди­электрической пружиной (рис. 7.21). Начальное расстояние между пластинами d₀,а после того, как конденсатор заря­дили, оно уменьшилось до величины d₁= d₀/2. Каким будет расстояние между пластинами конденсатора, если параллельно ему подключить такой же конденсатор, но неза­ряженный?

D2. Конденсатор емкостью С = 20 мкФ заряжен до напряжения U = 400 В. К нему подключается конденсатор емкости С₁ = 1,0 мкФ, в результате чего последний заря­жается. Затем, отключив этот конденсатор, заряжают таким же образом второй конденсатор с той же ем­костью (1,0 мкФ),третий и т. д. Затем конденсаторы сое­диняют последовательно. Какое максимальное напряжение можно получить таким способом?

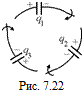
D3. Трем одинаковым изолирован­ным конденсаторам, емкости С каждый, были сообщены заряды q₁, q₂и q₃ (рис. 7.22). Конденсаторы соединили. Най­ти новые заряды на конденсаторах.

D4. Два одинаковых плоских конденсатора с пло­щадью пластин S соединены параллельно, заряжены до разности потенциалов V₀ от батареи и затем отключены от нее. Пластины одного из конденсаторов начинают сближать так, что расстояние между ними изменяется во времени по закону 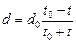, где d₀ — первоначальное расстояние между пластинами, t – время, t₀ – некоторая постоянная величина. Опре­делить ток I в проводах, соединяющих конденсаторы.

D5. Два плоских конденсатора емкости С каждый, соединенные параллельно и заряженные до напряжения U, отсо­единяют от источника. Пластины одного из конденсаторов могут двигаться свободно навстречу друг другу. Найти их скорость в момент, когда зазор между пластинами конден­сатора уменьшится в два раза. Масса каждой пластины равна М. Силой тяжести пренебречь.