Задачи средней трудности

В1. Обкладки конденсатора емкостью С, заряженного доразности потенциалов U, соединяются с обкладками такого же, но не заряженного конденсатора. Какое максимальное количество теплоты может выделиться в проводниках, соединяющих конденсаторы? Зависит ли полное количество выделившейся энергии от сопротивления проводников? Что происходит при изменении сопротивления проводников, соединяющим конденсаторы?

В2. Конденсатор емкостью С₁= 2,0 мкФ заряжают до напряжения U₁= 110 В. Затем, отключив от сети, его присоединяют к незаряженному конденсатору неизвестной емкости С₂, который при этом заряжается до напряжения U₂ = 44 В. Определить емкость С₂ второго конденсатора.

В3. Конденсатор емкостью С₁зарядили до напряжения U₁= 500 В При параллельном подключении этого конденсатора к незаряженному конденсатору емкостью С₂ = 4 мкФ вольтметр показал U₂ = 100 В. Найти емкость С₁.

В4. К воздушному конденсатору, заряженному до напряжения 210 В, присоединили параллельно такой же незаряженный конденсатор, но с диэлектриком из стекла. Какова диэлектрическая проницаемость данного сорта стекла, если напряжение на зажимах батареи оказалось равным 30 В?

В5. Конденсатор емкости C₁ = 20 мкФ, заряженный до разности потенциалов U₁ = 100 B, соединили параллельно с заряженным до разности потенциалов U₂ = 40 В конден­сатором, емкость которого С₂неизвестна (соединили одно­именно заряженные обкладки конденсаторов). Найти ем­кость C₂второго конденсатора, если разность потенциалов между обкладками конденсаторов после соединения ока­залась равной U = 80 В.

В6.Конденсатор неизвестной емкости с напряжением на обкладках U₁ = 1000 В соединили параллельно с другим конденсатором емкостью С₂ = 2,0 мкФ и напряжением на обкладках U₂ = 400 В. Какова емкость первого конденсатора, если после соединения напряжение стало U = 570 В? Определить общий заряд.

В7. Конденсатор, заряженный до разности потенциалов U₁ = 1,0×10² В, соединяется одноименно заря­женными обкладками с конденсатором удвоенной электроемкости, заряженным до разности потенци­алов U₂ = =0,40×10² В. Определить отношение энергий си­стемы до и после соединения обкладок.

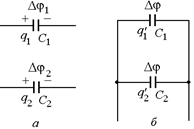Рис. 7.10

В8. Конденсаторы, емкости которых С₁ = 2,0 мкФ и С₂ = 0,5 мкФ, заряжены до разности потенциалов соотве­тственно U₁ = 1,00×10² В и U₂ = =0,50×10² В (рис. 7.10). Какое количе­ство теплоты выделится, если эти конденсаторы соединить одноименно заряженными пластинами?

В9. Два плоских конденсатора емкостями С₁ и С₂, обладающих зарядами q₁ и q₂, включают в замкнутую цепь так, что положительно заряженная пластина одного конденсатора соединяется с отрицательно заряженной пластиной другого. Определить заряд каждого конденсатора в этом случае.

В10. Конденсатор емкости С₁,имею­щий заряд q₁,соединяют через резистор с конденсатором емкости С₂,имеющим заряд q₂. Какое количество теплоты Q выделяется на резисторе? Соединяются противоположно заряженные обкладки.

В11.Конденсатор емкости C₁ = 4,0 мкФ, заряженный до разности потенциалов V₁ = 10 В, соединен параллельно с заряженным до разности потенциалов V₂ = 20В конден­сатором емкости С₂ = 6,0 мкФ (соединили разноименно заряженные обкладки конденсаторов). Какой заряд окажется на пластинах первого конденсатора после соединения?

В12. Конденсатор емкости С₁ = 1,0 мкФ, заряженный до разности потенциалов V₁ = 100 В, соединили с конденса­тором емкости С₂ = 2,0 мкФ, разность потенциалов V₂на обкладках которого неизвестна (соединили разноименно заряженные обкладки конденсаторов). Найти разность потенциалов V₂,если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V = 200 В.

В13. Конденсатор емкостью С₁= 1,0 мкФ, заряженный до разности потенциалов U₁= 100 В и отключенный от источника, соединили параллельно с конденсатором емкостью С₂= 3,0 мкФ, заряженным до разности потенциалов U₂= 60 В. Определить заряд каждого из конденсаторов и разность потенциалов между обкладками после их соединения, если соединяются обкладки, имеющие разноименные заряды.

В14.Два одинаковых плоских конденсатора соединены параллельно и заряжены до разности потенциалов U = 150 В. Определить разность потенциалов на конденсаторах U₁, если после отключения их от источника тока у одного конденсатора уменьшили расстояние между пластинами в два раза.

В15. Два изолированных плоских конденсатора емко­стью С_о каждый заряжены до разности потенциалов V_o и соединены параллельно. В одном из конденсаторов расстояние между пластинами увеличено в три раза. Найти заряды конденсаторов и напряжение на них.

В16. Два одинаковых плоских конденсатора (емкость каждо­го С = =0,01 мкФ) соединили параллельно, зарядили до напряже­ния U = 300В и отключили от источника. Затем пластины одного из конденсаторов раздвинули на расстояние, вдвое большее первоначального. Какой заряд протечет при этом по соединительным проводам?

В17. Система состоит из двух параллельно соединенных плоских воздушных конденсаторов, емкость каждого из которых С = 300 пФ. Систему зарядили до напряжения U = 1000 В и отключили от источника тока. На какую величину DW изменится энергия этой системы, если пластины одного из конденсаторов раздвинуть так, чтобы расстояние между ними увеличилось в 3 раза (рис. 7.11)?

Рис. 7.11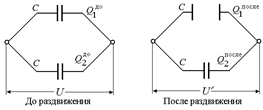

В18. Три последовательно соединенных конденсатора с емкостями С₁ = 100 пФ, С₂ = 200 пФ, С₃ = 500 пФ подключены к источнику тока, который сообщил им заряд q = 10 нКл. Найти напряжения на конденсаторах U₁, U₂ и U₃, напряжение источника тока V₀ и емкость всех конденсаторов С₀.

В19. Три конденсатора емкостями 1,0, 2,0 и 3,0 мкФ соеди­нены последовательно и присоединены к источнику напря­жения с разностью потенциалов 220 В. Каковы заряд и напряжение на каждом конденсаторе?

В20. Два плоских воздушных конденсатора с одинако­выми емкостями С = 10 пФ соединены последовательно. Насколько изменится емкость конденсаторов, если про­странство между пластинами одного из них заполнить диэлектриком с диэлектрической проницаемостью e = 2,0?

В21. Два последовательно соединен­ных конденсатора подключены к ис­точнику тока с напряжением U = 200 В (рис. 7.12). Один конденсатор имеет постоянную емкость C₁ = 0,50 мкФ, а другой – переменную емкость С₂(от C_min = 0,050 мкФ до С_mах = 0,50 мкФ). В каких пределах изменяется напряжение на переменном конденсаторе при изменении его емкости от минимальной до максимальной?

В22. Два плоских воздушных конденсатора с одинако­выми емкостями соединены последовательно и подключены к источнику тока. Пространство между пластинами одного из конденсаторов заполняют диэлектриком с диэлектриче­ской проницаемостью e = 9. Во сколько раз изменится напряженность электрического поля Е в этом конден­саторе?

В23. Решить предыдущую задачу для случая, когда конденсаторы после зарядки отключаются от источника тока.

В24. Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены к источнику тока. Во сколько раз изменится напряженность электриче­ского поля в одном из них, если другой заполнить диэлектриком с диэлектрической проницаемостью e = 4?

В25. Два последовательно соединенных конденсатора с емкостями C₁ = l мкФ и С₂ = 2 мкФ подключены к источнику тока с напряжением U = =900 В. Возможна ли работа такой схемы, если напряжение пробоя конден­саторов U_пр = 500 В?

В26. Два плоских конденсатора емкостями С₁ = 600 сми С₂ = 1500 смс изолирующим слоем из прессшпана толщиной 2 мм, соединенные последовательно, пробиваются при напряжении U = 5600 В. Определить напряженность поля, при которой происходит пробой прессшпана.

В27.Бумага пробивается при напряженности поля Е = 18 кВ/см. Два плоских конденсатора с изолирующим слоем из этой бумаги толщиной d = 2,0 мм, один емкостью С₁ = 1200 пФ, другой емкостью С₂ = 400 пФ, соединены последовательно. При каком наименьшем напряжении будет пробита эта система?

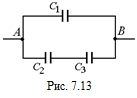
В28. Емкость батареи конденсаторов (рис. 7.13) равна 5,8 мкФ.Каковы емкость и заряд первого конденсатора, если С₂ = 1,0 мкФ, С₃ = = 4,0 мкФ, а подведенное к точкам А и В напряжение 220 В?

Задачи трудные

С1. Электроны, вылетающие без начальной скоро­сти с одной из пластин заряженного плоского конден­сатора, достигают другой пластины, имея скорость υ₁. Как изменится конечная скорость электронов, если па­раллельно к этому конденсатору подсоединить незаря­женный конденсатор вдвое большей емкости?

С2.Найти количество теплоты Q,выделившееся при соединении верхних незаземленных обкладок конденсаторов с емкостями С₁ = 2,0 мкФ и С₂ = 0,50 мкФ (рис. 7.14). Разности потенциалов между верхними обкладками конденсаторов и землей V₁ = 100 В и V₂ = –50 B.

Рис. 7.14 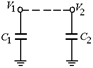Рис. 7.15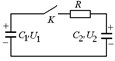

C3. Конденсаторы емкостью С₁ = 20 мкФ и С₂ = 60 мкФ, заряженные до напряжений U₁ и U₂, полярность которых указана на рис. 7.15, включены последовательно с ключом К и сопротивлением R = 80 Ом. В момент замыкания ключа по сопротивлению начинает протекать ток силой I = 0,20 А. Какое количество тепла Q выделится в сопротивлении к моменту, когда ток в нем прекратится?

С4. Конденсатор, заряженный до разности потенциа­лов V₁ = 20 В, соединили параллельно с заряженным до разности потенциалов V₂ = 4 В конденсатором емкости C₂ = 33мкФ (соединили разноименно заряженные обкладки конденсаторов). Найти емкость С₁первого конденсатора, если разность потенциалов между обкладками конденса­торов после их соединения V = 2В.

С5.Два конденсатора емкостью С₁= 0,1 мкФ и С₂ =0,2 мкФ,заряженные соответственно до напряжения U₁ = 100 В и U₂ = 200 В, соединили друг с другом противоположно заряженными обкладками с помощью проводников с большим сопротивлением R = 1000 Ом. Какой заряд протечет через каждое сопротивление R?

С6. Два одинаковых конденсатора с воздушным зазором между пласти­нами (емкость каждого С = 0,1 мкФ) соединили параллельно, зарядили до напряжения U = 300 В и отключили от источника тока. Затем один конденсатор залили керосином (e = 2). Какой заряд протечет при этом по соединительным проводам?

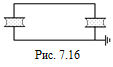С7. Два одинаковых конденсатора заполнены жидким диэлектриком с диэлектрической проницаемостью e (рис. 7.16). Конденсаторы соединены друг другом параллельно и заряжены до разности потенциалов V. Как изменится разность потенциалов, если из одного конденсатора вытечет диэлектрик? Как изменится разность потенциалов в батарее из п одинаковых параллельно соединенных конденсаторов, заряженной до разности потенциалов V, если из одного конденсатора вытечет диэлектрик?

С8. Два одинаковых плоских конденсатора емкости С соединены параллельно и заряжены до разности потенци­алов U. Пластины одного из конденсаторов разводят на большое расстояние. Найти разность потенциалов на втором конденсаторе и его энергию.

С9.Три последовательно соединенных конденсатора с емкостями С₁ = 0,10 мкФ, С₂ = 0,25 мкФ и С₃ = 0,50 мкФ под­ключены к источнику тока с напряжением U = 32 В. Найти напряжения U₁, U₂и U₃на конденсаторах.

C10. Два плоских конденсатора емкости С₁и С₂ каждый соединили последовательно, наложили на них разность потенциалов U и отключили от источника. Какова будет разность потенциалов между пластинами конденсаторов, если их пересоединить параллельно?

с11.Два одинаковых воздушных конденсатора емко­сти С = 100 пФ соединены последовательно и подключены к источнику тока с напряжением V = 10 В. Как изменится заряд на конденсаторах, если один из них погрузить в диэлектрик с диэлектрической проницаемостью e = 2,0?

С12. Бумажный конденсатор емкости С₁ = 5,0 мкФ и воз­душный конденсатор емкости С₂ = 30 пФ соединены по­следовательно и подключены к источнику тока с напряже­нием V = 200 В. Затем воздушный конденсатор заливается керосином (диэлектрическая проницаемость e = 2,0). Какой заряд q протечет при этом по цепи?

С13. Батарея из п последовательно соединенных одинаковых конденсаторов заряжена до разности потенциалов V. Конденсаторы заполнены жидким диэлектриком с диэлектрической проницаемостью e. Как изменится разность потенциалов, если из k конденсаторов вытечет диэлектрик? Конденсаторы отсоединены от источника тока.

С14.Два конденсатора соединены последовательно. Емкос­ти конденсаторов равны C₁и С₂. К какому напряжению U_максможно подключать эту батарею, если каждый из конденсаторов выдерживает напряжения U₁и U₂соответственно?

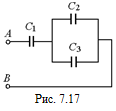С15. Три конденсатора с емкостью С₁ = 0,20 мкФ, С₂ = С₃ = 0,40 мкФ соединены по схеме, изображенной на рис. 7.17, и подключены к источнику постоянного напряжения U_АВ = 250 В. Найти общий заряд, заряды и разности потенциалов на отдельных конденсаторах. Определить электрическую энергию, запасенную батареей конденсато­ров.

Рис. 7.18

С16.Четыре конденсатора емкостями С₁ = 1,0 мкФ, С₂ = 1,0 мкФ, С₃ =3,0 мкФ, С₄ = 2,0 мкФ соединены, как показано на рис. 7.18. К точкам А и В подводится напряжение U = 140 В. Найти заряд q_i и напряжение U_i на каждом конденсаторе.

С17. Три конденсатора с емкостями С₁ = 1,0 мкФ, С₂ = 2,0 мкФ и С₃ = = 3,0 мкФ, имеющие максимально допустимые напряжения соответственно U₁ = 1000 В, U₂= 200 В и U₃= 500 В, соединены в батарею. При каком соединении конденсаторов можно получить наибольшее напряжение? Чему равны напряжение и емкость батареи?

С18.У трех конденсаторов емкости равны С, 2С и 3С, а пробойные напряжения соответственно V, V/4 и V/2.При каком из всех возможных способов соеди­нения батарея из этих трех конденсаторов выдержит наибольшее напряжение?

С19. Как изменятся заряд и разность потенциалов обкла­док конденсатора С₃ (рис. 7.19) при пробое конденсатора С₂? Во сколько раз? C₁ известно.

Рис. 7.19 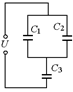Рис. 7.20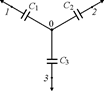

С20. В некоторой цепи имелся участок, показанный на рис. 7.20. Потенциалы точек 1, 2, 3 равны j₁, j₂, j₃, а емкости конденсаторов равны С₁, С₂, С₃. Найти потенциал точки 0.

С21. Двум плоским одинаковым конденсаторам, соеди­ненным параллельно, сообщен заряд Q. В момент времени t = 0 расстояние между пластинами первого конденсатора начинает равномерно увеличиваться по закону d₁ = d₀ + υt, а расстояние между пластинами второго конденсатора равномерно уменьшаться по закону d₂ = d₀ – υt. Пренебрегая сопротивлением подводящих проводов, найти силу тока в цепи во время движения пластин конденсаторов.