Последовательное соединение конденсаторов

Конденсаторы, у которых одна пластина каждого пре­дыдущего соединена только с одной пластиной последующего конденса­тора, называются соединенными последовательно.

Задача 7.7. Вычислить емкость системы из N конденсаторов, изображенной на рис. 7.5.

С1, С2, …, СN	Рис. 7.5
Ссист = ?

Решение.Пусть на клеммы системы подана разность потенциалов U = φ₁ – φ₂ > 0.

Рис. 7.6

Рассмотрим конденсатор С₁. Пусть на левую пластину конденсатора С₁поступил заряд +Q₁. Заряд распределился по плоскости пластины равномерно и создал вокруг себя поле напряженностью (рис. 7.6).

Под действием этого поля на поверхности второй пластины соберутся отри­цательные заряды.

Автор: Как Вы думаете, какой по вели­чине заряд соберется на поверхности второй пластины?

Читатель: Такой, чтобы поле внутри металла второй (а также и первой) пластины было равно нулю, поскольку электрическое поле внутри проводника в отсутствие тока всегда равно нулю. А для этого необходимо, чтобы заряд второй пластины (–Q₁) был равен по величине заряду первой пластины +Q₁. Ведь пластины одного и того же конденсатора абсолютно одинаковы по форме и размерам, поэтому поля зарядов +Q₁и –Q₁будут полностью компенсировать друг друга внутри пластин (см. рис. 7.6).

Автор: Совершенно верно.

Отметим, что правая пластина первого конденсатора и левая пластина второго конденсатора образуют единый проводник, который в целом должен быть электрически нейтральным (см. рис. 7.5), т.е. (+Q₂) + (–Q₁) = 0,откуда Q₂ = Q₁. Рассуждая аналогич­но, получим: Q₃ = Q₂, Q₄ = Q₃, …, Q_N = Q_N–1.

Вывод: заряды на пластинах всех последовательно соединенных конденсаторов одинаковы по величине:

Q₁ = Q₂ =…= Q_N = Q.

Заметим, что работа поля по перемещению единичного поло­жительного заряда через систему конденсаторов из точки 1 в точку 2 равна сумме работ по перемещению заряда от положительно заряженной пластины до отрицательно заряженной пластины внутри каждого конденсатора (см. рис. 7.5). (Ведь вне конденсаторов поле равно нулю). А так как разность потенциалов между двумя точками – это и есть работа по перемещению единичного положительного заряда между этими точками, то

U = U₁ + U₂ + … + U_N.

Вычислим емкость системы

Ответ: = .

Итак, запомним: емкость системы из N последовательно соединенных конденсаторов вычисляется по формуле

= . (7.2)

Задача 7.8.Два последовательно соединенных конденсатора емкостями С₁ и С₂ присоединены к источнику тока (рис. 7.7). Напряжение на первом конденсаторе U₁. Определить напряжение на втором конденсаторе U₂ и напряжение источника U.

С1 С2 U1	Рис. 7.7	Решение. U = U1 + U2, (1) Q1 = C1U1, (2) Q2 = C2U2, (3) Q1 = Q2. (4)
U2 = ? U = ?

Из (4) имеем С₁U₁ = C₂U₂, отсюда 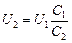. Подставляя U₂ в (1), получим:

.

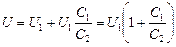Ответ: ; .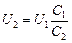

СТОП! Решите самостоятельно: А13, В19–В21, С10.

Задача 7.9. Два одинаковых конденсатора соединены последовательно и подключены к источнику напряжения. Во сколько раз изменится разность потенциалов на втором конденсаторе, если первый погрузить в жидкость с диэлектрической проницаемостью e?

e	Решение. Пусть напряжение, поданное на систему конденсаторов, равно U. Тогда напряжения на каждом конденсаторе .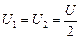
п = =?

Пусть после погружения первого конденсатора в диэлектрик напряжения на конденсаторах равны и 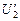. Так как конденсаторы по-прежнему подключены к источнику напряжения, то

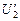+ = U. (1)

А поскольку конденсаторы соединены последовательно, то их заряды равны

. (2)

Если емкость каждого конденсатора сначала была равна С, то после погружения в диэлектрик емкость первого конденсатора увеличилась в e раз и стала равна eС. Тогда из (2) следует

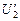eС = С . (3)

Выразим из (3) и подставим в (1), получим

.

Отсюда п = .

Ответ: п = .

СТОП! Решите самостоятельно: В22, В23, С12, С13.