Параллельное соединение конденсаторов

ПАРАЛЛЕЛЬНОЕ И ПОСЛЕДОВАТЕЛЬНОЕ

СОЕДИНЕНИЯ КОНДЕНСАТОРОВ

Система конденсаторов

Пусть произвольное число различных конденсаторов произволь­ным образом соединено в некоторую систему (рис. 7.1). Подадим на клеммы этой незаряженной системы разность потенциалов: U = φ₁ – φ₂ > 0.Тогда через клеммы системы под действием внешнего по­ля пройдут и осядут на прилегающих обкладках конден­саторов одинаковые по величине разноименные заряды +Q и –Q. Ведь ток через систему не идёт, а в целом система электрически нейтральна.

Величина С_сист = Q/U называется емкостью системы конденсаторов.

Иначе: емкостью системы конденсаторов С_систназывается физическая величина, равная емкости такого конденсатора, у которого отношение величины заряда, помещенного на пластины к разности по­тенциалов между ними в точности равно отношению величины заряда, прошедшего через клеммы системы к поданной на клеммы разности потенциалов.

Параллельное соединение конденсаторов

Конденсаторы, у которых все противоположные обклад­ки соединены между собой, называются соединенными параллельно.

Задача 7.1. Вычислить емкость системы N конденсаторов C₁, C₂, …, C_N, изображенной на рис. 7.2.

C1, C2, …, CN	Решение. Подадим на клеммы системы разность потенциалов U. Приэтом все левые пластины конденсаторов, образyют один проводник, а все правые – другой.	Рис. 7.2
Ссист = ?

Поскольку ток в системе не течет, то поверхности обоих проводников – эквипотенциальны, а следовательно, разности потенциалов между пластинами каждого конденсатора одинаковы и равны: U₁= U₂ = ... = U_N = U. Заряды на конденсаторах при этом, вообще говоря, разные: Q₁, Q₂, …, Q_N. Сумма всех зарядов на одноименно заряженных пластинах равна общему заряду Q, поступившему на эти пластины через клеммы системы при подаче напряжения: Q = Q₁ + Q₂ +…+ Q_N. Тогда

.

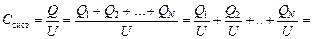
Ответ: .

Итак, запомним, что емкость системы из N параллельно соединенных конденсаторов вычисляется по формуле

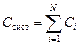. (7.1)

Задача 7.2. Два конденсатора емкостями С₁ = 2,0 мкФ и С₂ = = 4,0 мкФ соответственно соединены параллельно. Заряд первого конденсатора q₁ = 1,0 нКл. Определить заряд второго конденсатора.

С1 = 2,0 мкФ С2 = 4,0 мкФ q1 = 1,0 нКл	Решение. Напряжения на параллельно соединенных конденсаторах равны: U1 = U2, тогда .
q2 = ?

Ответ: .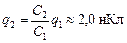

СТОП! Решите самостоятельно: А1–А5.

Задача 7.3. Конденсатор емкостью С₁ = 6,0 мкФ и напряжением на обкладках U₁ = 4,0×10² В соединили параллельно с незаряженным конденсатором емкостью С₂ = 10,0 мкФ. Какая разность потенциалов установилась на обкладках обоих конденсаторов? Как распределился заряд?

С1 = 6,0 мкФ U1 = 4,0×102 В С2 = 10,0 мкФ	Решение. Заряд первого конденсатора частично перешел на второй, но общая величина заряда не изменилась: qдо = qпосле Þ C1U1 = CобщU = (C1 +С2)U Þ .
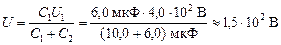U = ? q1 = ? q2 = ?

Заряды на конденсаторах при этом стали равны

q₁ = C₁U = 6,0×10^–6 Ф × 1,5×10² В » 9,0×10^–4 Кл = 0,90 мКл,

q₂ = C₂U = 10,0×10^–6 Ф × 1,5×10² В » 1,5×10^–3 Кл =1,5 мКл.

Ответ: ; q₁ = C₁U = 0,90 мКл;

q₂ = C₂U = 1,5 мКл.

СТОП! Решите самостоятельно: А6, В1, В2, В4.

Задача 7.4. Конденсатор емкостью С₁ = 3,00 мкФ заряжен до напряжения U₁ = 300 В, а конденсатор емкостью С₂ = 2,00 мкФ заряжен до напряжения U₂ = 200 В. После зарядки конденсаторы соединили одноименными полюсами. Какая разность потенциалов установится между обкладками после соединения? Какое количества тепла выделится при этом?

С1 = 3,00 мкФ U1 = 300 В С2 = 2,00 мкФ U2 = 200 В	Решение. Конденсаторы соединены параллельно, поэтому их общая емкость равна Собщ = С1 + С2, а общий заряд qобщ = q1 + q2 = C1U1 + C2U2. Тогда искомая разность потенциалов равна
U = ? Q = ?

260 В.

Энергия конденсаторов до соединения , после соединения:

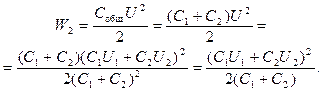
Искомое количество теплоты равно убыли энергии системы:

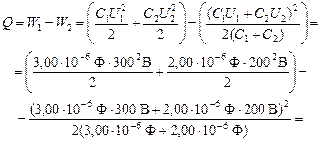
= 6×10^–3 Дж = 6 мДж.

Ответ: U » 260 В, Q » 6 мДж.

СТОП! Решите самостоятельно: А7, А8, В6, В7, С2.

Задача 7.5. Два конденсатора емкостями С₁ и С₂, заряженные до напряжений U₁ и U₂, соединили противоположно заряженными обкладками. Найти напряжение между противоположно заряженными обкладками получившейся системы.

С1 С2 U1 U2	Рис. 7.3
U = ?

Решение. До соединения заряды на обкладках были равны соответственно Q₁ = U₁С₁ и Q₂ = U₂С₂.

После соединения левые обкладки конденсаторов С₁ и С₂ стали представлять собой единый проводник с зарядом Q_общ = (Q₁ – Q₂), а правые – с зарядом –(Q_общ) = –(Q₁ – Q₂) (рис. 7.3). При этом конденсаторы оказались соединенными параллельно, и иско­мая разность потенциалов равна

U = |Q_общ|/C_общ,

где Q_общ = Q₁ – Q₂ = С₁U₁ – С₂U₂, а С_общ = C₁ + C₂.

Ответ: .

Замечание:знак модуля в выражении для U нужен для того, чтобы получить положительное значение напряжения для случая Q₁ < Q₂,т.е. С₁U₁ < C₂U₂,поскольку под напряжением мы всегда понимаем абсолютное значение разности потенциалов.

СТОП! Решите самостоятельно: А9, В9, В10, В13, С5.

Задача 7.6. Система состоит из двух параллельно соединенных плос­ких воздушных конденсаторов, емкость каждого из которых С = 300 пФ. Систему зарядили до напряжения U = 1000 В и отключили от источ­ника тока. На какую величину DW изменится энергия этой сис­темы, если пластины одного из конденсаторов раздвинуть так, чтобы расстояние между ними увеличилось в 2 раза (рис. 7.4)?

С = 300 пФ U = 1000 В d2 = 2d1	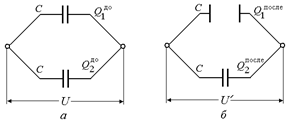Рис. 7.4
DW = ?

Решение.Энергия до раздвижения пластин

.

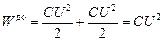После раздвижения пластин емкость первого конденсатора уменьшилась в 2 раза, а емкость второго не изменилась:

С₁ = С/2, С₂ = С. (1)

Поскольку конденсаторы соединены параллельно, напряжения на них равны как до,так в после раздвижения пластин:

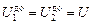, (2)

. (3)

Поскольку система отключена oт источника тока, суммарный заряд на одноименно заряженных обкладках не изменился:

. (4)

Учтем, что 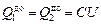, , 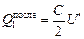, тогда из (4) получим CU + CU = 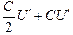, откуда

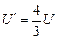. (5)

Энергия системы после раздвижения пластин:

Изменение энергии системы

.

Подставим численные значения

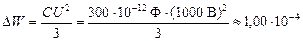Дж.

Ответ: 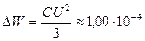Дж.

СТОП! Решите самостоятельно: В14–В16, С6, С8.