Частотный критерий устойчивости Михайлова
Заменим в полиноме А(р) 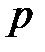 на
на 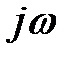 , тогда:
, тогда:
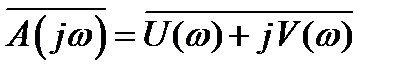 , (5.22)
, (5.22)
где U(ω) – вещественная часть полинома 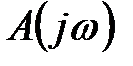 ,
,
V(ω)– мнимая часть полинома 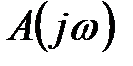 .
.
На комплексной плоскости он может быть представлен в виде вектора. При изменении 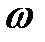 от
от 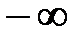 до
до 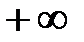 вектор
вектор 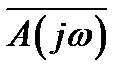 своим концом опишет в комплексной плоскости кривую, которая называется годографом Михайлова или характеристикой кривой. Поскольку функция
своим концом опишет в комплексной плоскости кривую, которая называется годографом Михайлова или характеристикой кривой. Поскольку функция 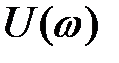 является чётной функцией
является чётной функцией  , а
, а 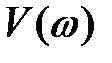 - нечётная, то годограф Михайлова симметричен относительно вещественной оси. Поэтому нет необходимости рассматривать весь годограф Михайлова, а достаточно рассмотреть лишь одну его часть, которая вычерчивает вектор
- нечётная, то годограф Михайлова симметричен относительно вещественной оси. Поэтому нет необходимости рассматривать весь годограф Михайлова, а достаточно рассмотреть лишь одну его часть, которая вычерчивает вектор 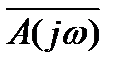 при изменении
при изменении 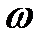 от 0 до
от 0 до 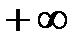 . Тогда из уравнения (5.21) следует, что для устойчивой системы приращение аргумента вектора
. Тогда из уравнения (5.21) следует, что для устойчивой системы приращение аргумента вектора 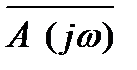 при изменении
при изменении 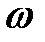 от
от 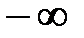 до
до 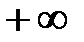 должно быть
должно быть
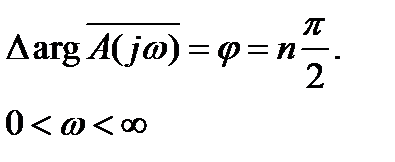
(5.23)
Полученное выражение и есть частотный критерий устойчивости Михайлова, в математической форме. Словами его можно выразить так
САУ устойчива тогда и только тогда, когда характеристический вектор при изменении  от 0 до
от 0 до  последовательно обходит число квадрантов, равное порядку характеристического уравнения, нигде не обращается в нуль.
последовательно обходит число квадрантов, равное порядку характеристического уравнения, нигде не обращается в нуль.
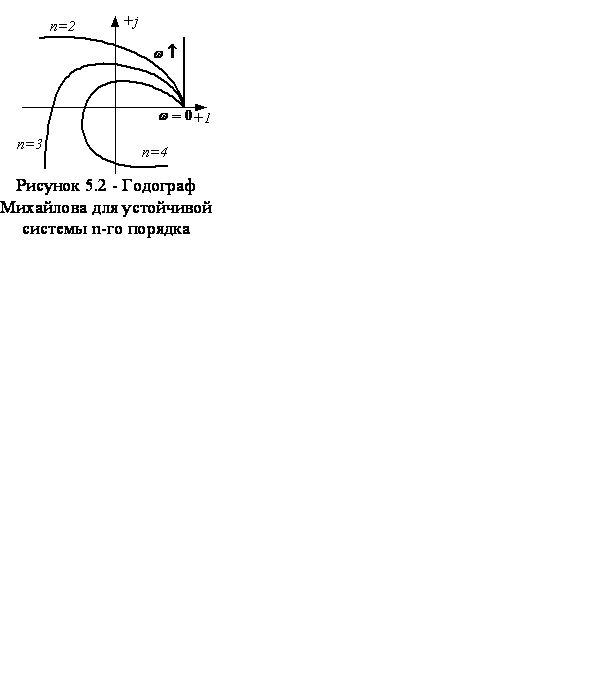
На рисунке 5.2 показаны годографы Михайлова для устойчивых систем при различных значениях n. Все они начинаются при ω=0 со значением а0 на положительной полуоси. Это означает, характеристические уравнения приведены к виду, при котором их коэффициенты положительны. Годографы, изображённые на рисунке 5.2 уходят в бесконечность при ω→∞ и обходят соответствующее число квадрантов.
Пример 5.3.
Определить устойчивость системы, характеристическое уравнение которой
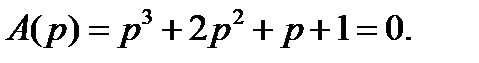
Заменим р на jω, получим
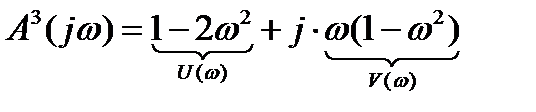 .
.
 Составим таблицу
Составим таблицу
| 
| 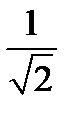
| 
| ||
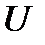 (ω) (ω)
| -1 | 
| |||
 (ω) (ω)
| 0,353 | 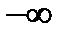
|
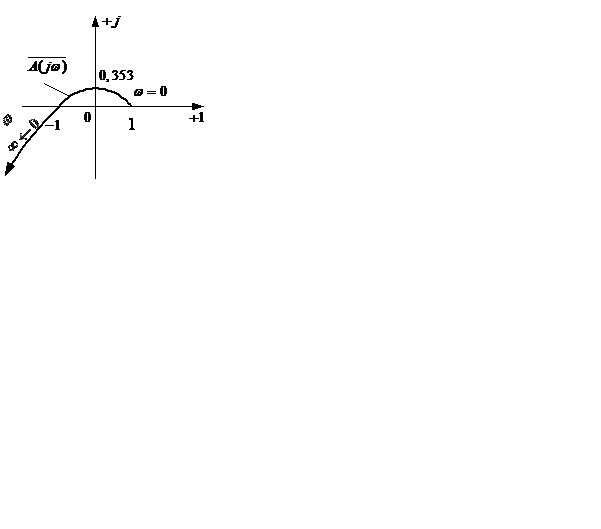
Рисунок 5.3
Построим годограф рисунок 5.3.
Система устойчива, поскольку годограф Михайлова огибает три квадранта (по числу равному порядку характеристического уравнения)
Пример 5.4.
Характеристическое уравнение системы 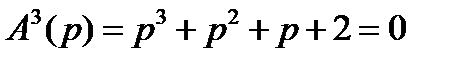 .
.
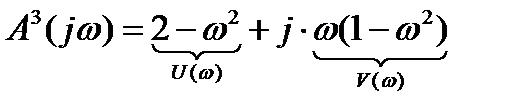 .
.
Проделав аналогичные расчеты, построим график рисунок 5.4.Система стала не устойчивая, поскольку годограф Михайлова огибает всего два квадранта (что не равно порядку характеристического уравнения).
Пример 5.5.
Характеристическое уравнение системы 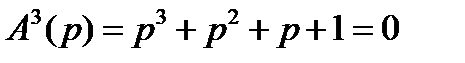 .
.
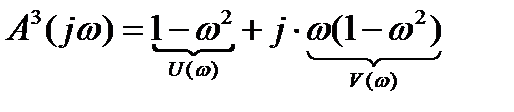 . Построим график рисунок 5.5. Система находится на грани устойчивости, поскольку
. Построим график рисунок 5.5. Система находится на грани устойчивости, поскольку годограф Михайлова огибает два квадранта вместо трёх и проходит через начало координат.
Дата добавления: 2016-04-11; просмотров: 822;
