Частотные критерии устойчивости. Принцип аргумента

Впервые были использованы частотные методы определения устойчивости Найквистом при исследовании электронных усилителей с отрицательной обратной связью. Для САУ впервые обосновал и обобщил частотные методы в 1938 году А.В.Михайлов (статья «Метод гармонического баланса в теории регулирования», «Автоматика и телемеханика» №3, 1938 год).

В основе критерия Михайлова лежит известный в теории функций комплексного переменного принцип аргумента.

Пусть дано характеристическое уравнение

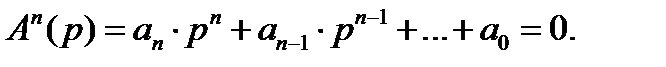(5.14)

Если заменить в 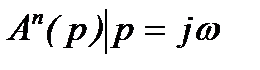, то получится характеристический вектор 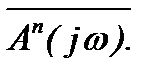При этом характеристический вектор может быть разложен на множители по теореме Виетта

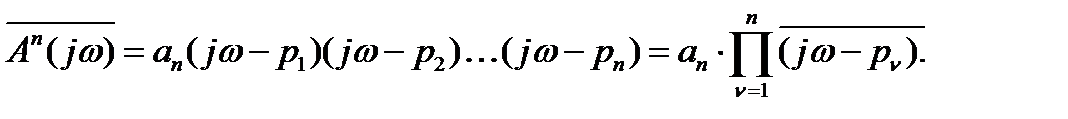(5.15)

Найдём аргумент комплексного числа

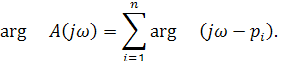
(5.16)

Изменение аргумента вектора 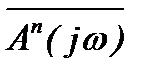при изменении 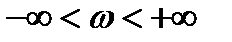равно

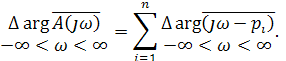
(5.17)

Согласно (5.17) для определения изменения аргумента необходимо подсчитать сумму изменений аргументов двучленов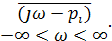

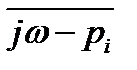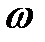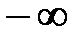В основу частотных критериев исследования устойчивости САУ положено следующее: если расположить корень р_i характеристического уравнения в комплексной плоскости и рассматривать вектор при изменении от до 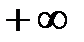, то каждый вектор 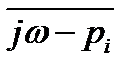повернется на угол

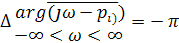, (5.18)

(рисунок 5.1, б), если корень р_i расположен в левой части комплексной полуплоскости; и на угол

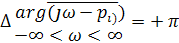, (5.19)

(рисунок 5.1, а), если корень р_i расположен в правой части комплексной полуплоскости.

Рисунок 5.1 – Принцип аргумента

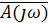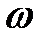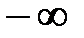Таким образом, если принять, что q корней характеристического уравнения n-порядка имеют положительную вещественную составляющую, а (n-q) – отрицательную, то характеристический вектор при изменении от до 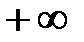получит приращение аргумента:

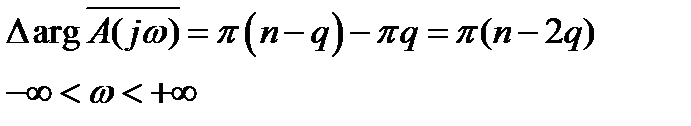. (5.20)

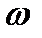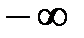Для устойчивой системы при изменении от до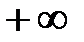

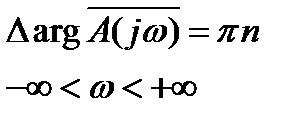. (5.21)

Выражения (5.20) и (5.21) и представляют собой запись принципа аргумента для характеристического полинома А(р).