Постановка задачи исследования устойчивости

Так же, как и в случае линейных звеньев, необходимым и достаточным условием устойчивости линейной системы автоматического регулирования является отрицательность вещественных частей всех корней её характеристического уравнения. Последнее может быть получено из передаточной функции замкнутой системы, связывающей любые её вход и выход, путём приравнивания нулю знаменателя передаточной функции.

На рисунке 5.1 показана структурная схема, к которой может быть приведена любая односвязная линейная система автоматического регулирования при отсутствии всех внешних воздействий, кроме задающего. Если передаточная функция разомкнутой системы

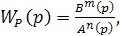(5.1)

где В^m(p) и Aⁿ(p) – полиномы степеней соответственно m и n (m≤n), то передаточная функция замкнутой системы

, (5.2)

откуда путём приравнивания знаменателя 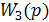нулю получается характеристическое уравнение замкнутой системы n – ой степени:

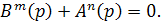(5.3)

Обозначая

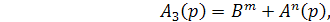(5.4)

можно записать характеристическое уравнение в виде

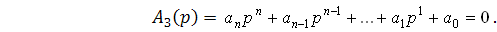(5.5)

Попытки анализа устойчивости линейных систем автоматического управления путём прямого отыскания корней характеристического уравнения наталкиваются на практические трудности, связанные с отсутствием аналитических выражений для корней степени выше четвёртой; для уравнений третьего и четвёртого порядков имеющиеся выражения малоудобны. Однако нет необходимости находить значения корней, поскольку для суждения об устойчивости системы нужно знать лишь, что все они расположены левее мнимой оси на плоскости комплексного переменного р. В теории автоматического управления пользуются условиями, которые позволяют судить о расположении корней в левой полуплоскости без нахождения их значений; эти условия называются критериями устойчивости.