Линеаризация статических характеристик
Применяют линеаризацию статическую и динамическую.
- Статическая линеаризация.
Рисунок 4.2 – Статическая (а) и динамическая (б) линеаризации
Кривая заменяется прямой (рисунок 4.2,а) в соответствии с каким-либо законом. Например, методом наименьших квадратов.
- Динамическая линеаризация.
В точке А кривой находится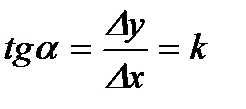 
и заменяется при этом кривая линейным законом (рисунок 4.2, б).
а) Функция одной переменной.
Пусть дана статическая характеристика – непрерывная дифференцируемая функция y =f(x), причем точкой основного режима работы является точка А.
Рисунок 4.3 – Динамическая линеаризация
Разложим функцию в степенной ряд Тейлора в рабочей точке А
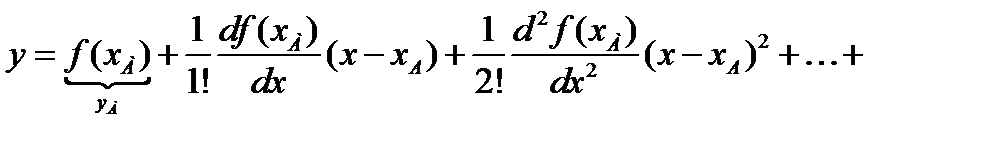(4.3)
.
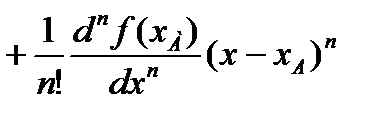При рассмотрении изменения x в окрестностях точки А в небольшом диапазоне возможно ограничиться рассмотрением 2-х первых членов ряда Тейлора
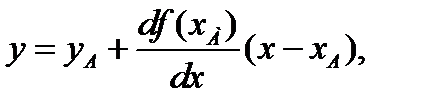
(4.4)
где x – xA = Δx – отклонение x от исходного значения;
y – yA = Δy – отклонение y от исходного значения.
Тогда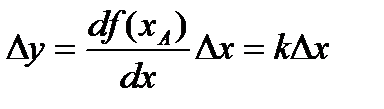 
,
где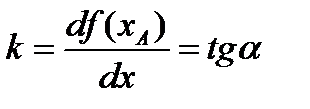 
– коэффициент связи между y и x в окрестностях точки А или коэффициент усиления элемента в окрестности исходной точки.
На структурной схеме последнее уравнение изобразится рисунок 4.4.
Рисунок 4.4
Пример 4.1. Дано уравнение y=x2+x+1 линеаризовать его в точке хА=1..
Находим производную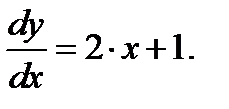 
Тогда k(А)=3. 
б) Функция двух переменных.
Пусть дана статическая характеристика в виде непрерывной дифференцируемой функции двух переменных (рисунок 4.5)
z = f(x,y).(4.5)
Точкой основного режима работы является точка А.
| | |
Рисунок 4.5 – Функция двух переменных
\
Разложим функция в степенной ряд Тейлора в точке А:
.
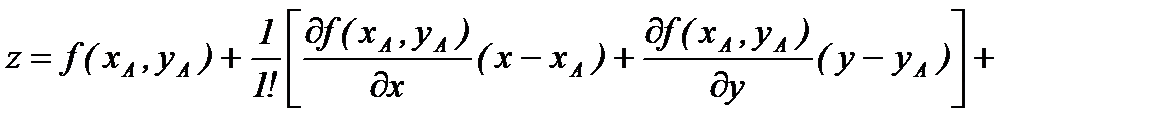
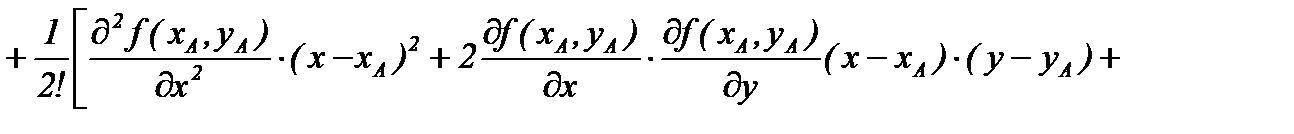
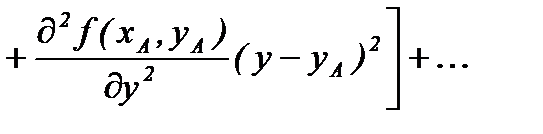(4.6)
При небольшом отклонении x, y от рабочей точки А также допустимо ограничение двумя членами ряда Тейлора
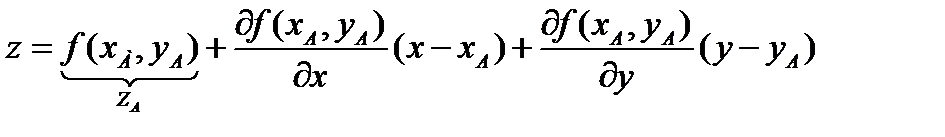. (4.7)
Обозначим
,
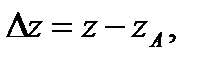
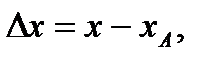
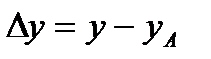тогда уравнение (4.7) запишется в виде
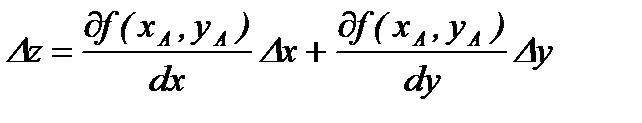. (4.8)
Обозначим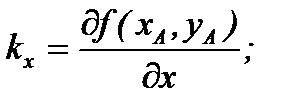 
.
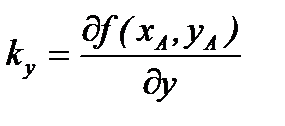На структурной схеме это уравнение отобразится (рисунок 4.6)
Рисунок 4.6
Пример 4.2. Дана функция z=2x2+y+3, линеаризовать её в точке хА=1; уА=2.
Найдём частные производные
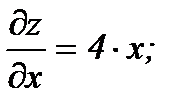
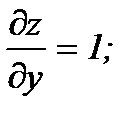тогда kx=4; ky=2.
4.3 Передаточная функция в установившемся режиме
Структурная схема для установившегося режима составляется на основе уравнений элементов САУ в статике или на основе линеаризованной структурной схемы САУ формальным путём приравнивания оператора p к нулю.
Пример 4.3. Дана структурная схема САУ. Вычислить общий коэффициент усиления (передаточную функцию в установившемся режиме).
Поведение системы в переходном процессе (в динамике) происходит в соответствии передаточной функцией
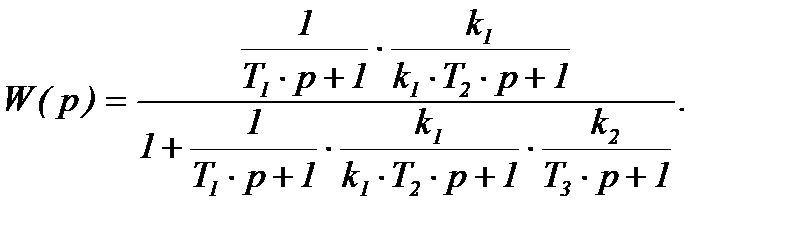
Общий коэффициент усиления (установившийся режим) получим, заменяя р на нуль.
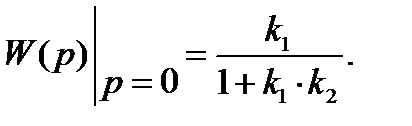
Дата добавления: 2016-04-11; просмотров: 1032;