Влияние коэффициента замкнутого контура

Пусть задана статическая система (рисунок 4.7).

Рисунок 4.7 – Статическая система автоматического управления

По задающему воздействию в разомкнутой САУ (без ОС) изменение выходного сигнала равно

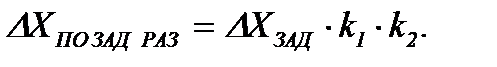(4.9)

В замкнутой САУ это изменение равно 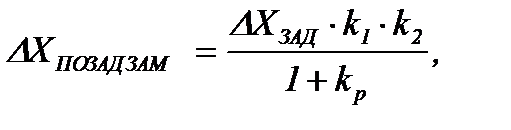(4.10)

где k_p=k₁k₂k₃.

По возмущающему воздействию в разомкнутой САУ изменение выходного сигнала равно

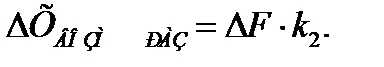(4.11)

В замкнутой САУ

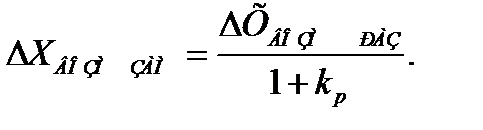(4.12)

Отсюда можно сделать вывод. В замкнутой статической системе отклонение, как по задающему, так и по возмущающему воздействию в (1+k_P) раз меньше, чем в разомкнутой системе без ОС (рисунок 4.8).

Рисунок 4.8

В астатической САУ (рисунок 4.9) отклонение выходного сигнала по возмущающему воздействию составит

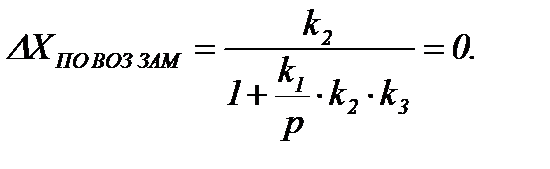
Рисунок 4.9

Устойчивость САУ

Основной динамической характеристикой автоматической системы является её устойчивость.

Устойчивостью называют свойство САУ возвращаться к последующему установившемуся состоянию после приложения возмущающего воздействия, которое вывело её из состояния равновесия.

Системы АУ, обладающие указанным свойством, называют устойчивыми. Системы, в которых не восстанавливается равновесный режим, а при отклонениях от него регулируемая величина начинает неограниченно возрастать или совершать колебания с возрастающей амплитудой, называют неустойчивыми.

Обеспечение устойчивости является необходимым условием работоспособности.

Поэтому исследование САУ на устойчивость представляет собой одну из основных задач в ТН.

Различают два вида устойчивости: устойчивость в «малом» и устойчивость в «большом».

САУ называют устойчивой в «малом», если устойчивость проявляется в результате бесконечно малых изменений возмущающего воздействия. В том случае, когда система сохраняет устойчивое состояние при достаточно больших, конечных по величине изменениях возмущающего воздействия, то САУ называют устойчивой в «большом».

Для линейных систем регулирования требования устойчивости в «малом» является необходимым и достаточным условием устойчивости в «большом». Для нелинейной системы устойчивость в «малом» в общем случае не означает, что она устойчива в «большом».

Исследования устойчивости в «малом» представляют большой практический интерес, так как во многих случаях на основании его можно сделать вывод об устойчивости в «большом» реальных, в том числе и нелинейных систем.

Для ответа на эти и другие вопросы целесообразно разобраться в физике образования колебаний САУ. Причиной неустойчивости замкнутых САУ является наличие в них элементов, способных запасать энергию. В электрических цепях такими аккумуляторами являются индуктивности и ёмкости. В механических системах ту же роль играют движущиеся массы, обладающие механической инерцией.

В электромеханических системах, системах электропривода такими накопителями энергии являются как индуктивности и ёмкости, так и движущиеся массы.

В замкнутых САУ часть энергии с выхода передаётся на вход системы. Если бы передача энергии совершалась без задержки времени, что реально невыполнимо, то, по-видимому, проблемы обеспечения устойчивости не было бы. Применение безынерционных аппаратов – вентильных преобразователей, полупроводниковых и вентильных усилителей и так далее способствует инерционности САУ электропривода.

Причину неустойчивости легко уяснить себе также исходя из частотной характеристики. Пусть к системе приложен синусоидально заданный сигнал, обратная связь не подсоединена.

При некоторой определённой частоте и при наличии инерционных элементов колебания 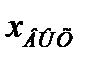могут отставать от колебаний 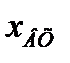на 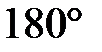. Если теперь замкнуть систему отрицательной обратной связью, то сигнал обратной связи будет складываться с заданным сигналом, то есть увеличивать его вместо того, чтобы уменьшать.

Если же замыкая обратную связь отключить входной сигнал, если 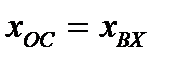(по амплитуде), то возникшие колебания в системе будут поддерживаться сами собой. Если при этом 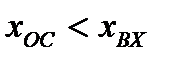(по амплитуде), то очевидно колебания затухнут.

Если 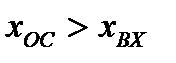(по амплитуде), то колебания в системе будут расходящимися.

При исследовании устойчивости могут преследоваться следующие задачи:

1. Выяснение, является ли устойчивой система при заданных параметрах.

2. Определение допустимых изменений параметров при инерционной системе с заданной структурой по условию сохранения устойчивости.

3. Анализ структуры и определение параметров САУ, при которых она может стать неустойчивой.