Частотный критерий Найквиста

Он позволяет судить об устойчивости замкнутой системы регулирования по устойчивости разомкнутой системы, не зная уравнения системы.

Подадим на вход разомкнутой системы синусоидальные колебания (j₀¢) от генератора синусоидальных колебаний (ГСК). Тогда с течением времени на выходе разомкнутой системы установятся также синусоидальные колебания регулируемого параметра j¢, но они будут иметь другую амплитуду и сдвиг по фазе j. Частотная передаточная функция разомкнутой системы будет

.

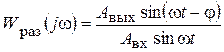Параметрами настройки регуляторов (k_р, Т_и) можно добиться, чтобы А_вых=А_вх (за это отвечает коэффициент усиления регулятора k_р) и j=-p (за это отвечает время интегрирования Т_и). Тогда, частотная передаточная функция будет

.

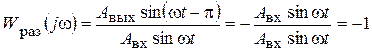Значение W_раз(jw)=–1 – указывает на границу устойчивости (рис. 72).

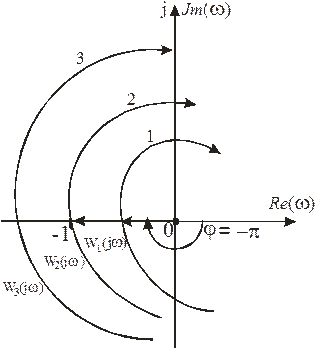
Представим W_раз(jw)=–1 на комплексной плоскости.

При сдвиге по фазе j=–p длина вектора W_раз(jw) определяет амплитудно-частотную характеристику разомкнутой системы .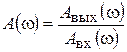

При А(w)=–1 система находится на границе устойчивости (кривая 2). При А(w)<–1 – система неустойчива (кривая 3), а при А(w)>–1 система устойчива (кривая 1). Из этих соотношений следует, что в устойчивых системах А_вых(w) < А_вх(w), то есть амплитуда колебаний уменьшается, а при А_вых(w) > А_вх(w) – нарастает – система неустойчива.

Замкнем систему отрицательной единичной обратной связью (показано на рис. 75 штриховой линией). Тогда передаточная функция замкнутой системы будет

.

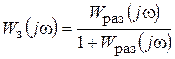Характеристическое уравнение замкнутой системы, записанное через передаточную функцию, будет

,

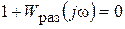из которого следует полученный ранее результат W_раз(jw)=–1, то есть замкнутая система находится на границе устойчивости, если частотная передаточная функция разомкнутой системы W_раз(jw) равна –1 в комплексной плоскости.

Если изменять частоту от 0 до +¥, то на комплексной плоскости получим годограф частотной передаточной функции разомкнутой системы W_раз(jw), которая является амплитудно-фазовой частотной характеристикой разомкнутой системы (АФЧХ). На комплексной плоскости показаны АФЧХ разомкнутых систем (1, 2 и 3).

Формулировка критерия Найквиста

Система автоматического регулирования, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если АФЧХ разомкнутой системы не охватывает точку с координатами (–1; j0).