Частотный критерий Михайлова
Он также основан на характеристическом уравнении системы
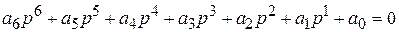
Заменой оператора р на jw, где w - частота колебаний, уравнение переводится в комплексный вид, и может быть представлено вектором в комплексной плоскости, которой называют вектором Михайлова (или вектором характеристической функции).
р®jw. Тогда получим
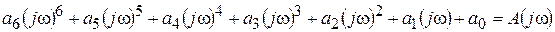 ,
,
А(jw) вектор Михайлова.
Члены с четной степенью дадут знакопеременный ряд действительных чисел, а члены с нечетными степенями – знакопеременный ряд комплексных чисел. Тогда
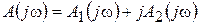 ,
,
где А1(w) – действительная часть; А2(w) –комплексная часть.
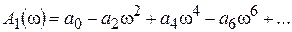
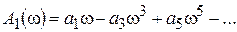
Если изменять частоту w от 0 до +¥, то конец вектора Михайлова в комплексной плоскости (А1, jА2) будет поворачиваться, изменяя свою длину, и опишет кривую, которую называют годографом Михайлова (или годографом вектора характеристической функции).
Формулировка устойчивости по критерию Михайлова:
Система автоматического регулирования будет устойчивой, если при изменении частоты от нуля до бесконечности, годограф Михайлова обходит последовательно в положительном направлении (то есть против часовой стрелки), n – квадрантов комплексной плоскости, где n – степень характеристического уравнения системы (рис. 74).
| Рис. 74. Годограф Михайлова I, II, III и т.д. – номера квадрантов;1 – система устойчива; 2 – система неустойчива; 3 – система на границе устойчивости |
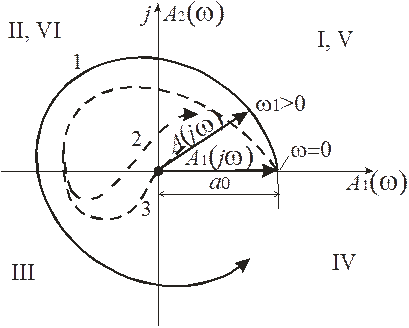 Если порядок прохождения квадрантов нарушается, система неустойчива (2); если годограф Михайлова проходит через нуль – система находится на границе устойчивости (3).
Если порядок прохождения квадрантов нарушается, система неустойчива (2); если годограф Михайлова проходит через нуль – система находится на границе устойчивости (3).
На практике, при решении задач устойчивости, достаточно найти частоты, при которых происходит пересечение годографа с осями координат. Для этого достаточно приравнять нулю вещественную и мнимую части вектора Михайлова.
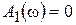 ,
, 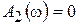 .
.
Расставив частоты по мере возрастания их значений, определяют значения А1 и А2. Если порядок пересечения годографа с осями координат чередуется по квадрантам (повторяет прохождение годографа) система устойчива, если порядок пересечения осей нарушается – система неустойчива.
Пример:
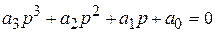 ;
;
р®jw; 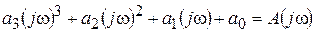 .
.
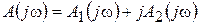 .
.
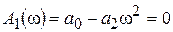 ;
; 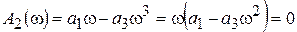 .
.
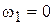 ;
; 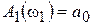 ;
; 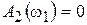 .
.
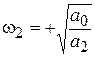 ;
; 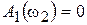 ;
; 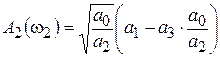 .
.
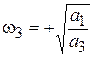 ;
; 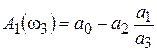 ;
; 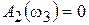 .
.
Дата добавления: 2016-04-11; просмотров: 864;
