Цепь синусоидального тока с индуктивностью
Если в цепь синусоидального тока включить катушку, с активным сопротивлением, которой можно пренебречь, то такую цепь можно рассматривать как цепь, обладающую только индуктивностью (рис.65). Синусоидальный ток, проходя через катушку, наводит в ней ЭДС самоиндукции, величина которой определяется выражением
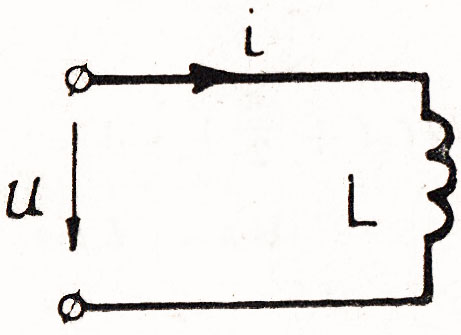
Рис. 65
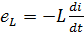 3.22
3.22
Примем начальную фазу тока равной нулю, тогда
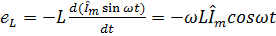 3. 23
3. 23
При cos 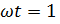 ЭДС самоиндукции будет иметь максимальное амплитудное значение
ЭДС самоиндукции будет иметь максимальное амплитудное значение
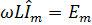 3. 24
3. 24
Учитывая, что косинусоиду можно рассматривать как синусоиду с начальной фазой  и принимая во внимание выражение 3. 24, получим
и принимая во внимание выражение 3. 24, получим
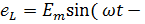
 ) 3. 25
) 3. 25
Так как активное сопротивление равно нулю, то согласно второму закону Кирхгофа сумма напряжений на зажимах цепи ЭДС самоиндукции равно нулю
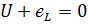
Отсюда 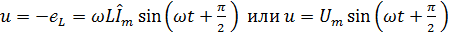 3. 26
3. 26
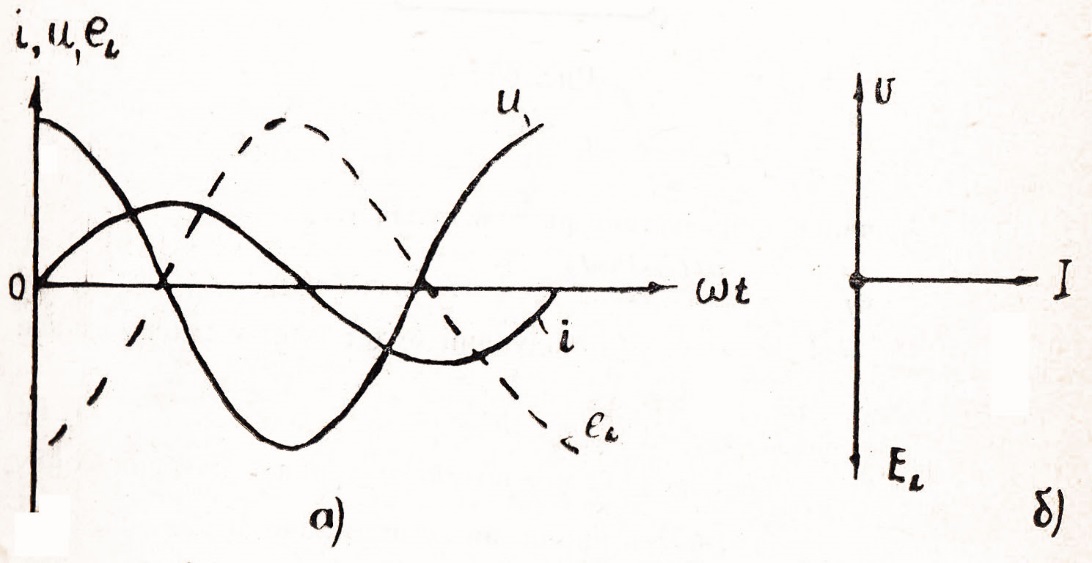
Из выражения 3. 26 видно, что в цепи с индуктивностью напряжение опережает ток на 90°. Приложенное к цепи напряжение вызывает в ней такой ток, который при своем изменении в любой момент времени индуктирует ЭДС, равную по величине и противоположную по знаку приложенному напряжению. На рис. 66 показаны волновая и векторная диаграммы токов и напряжений в цепи с индуктивностью.
Максимальное значение приложенного напряжения соответствует моменту, когда
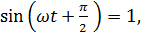 т.е.
т.е.
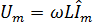 3. 27
3. 27
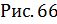
Разделив левую и правую части выражения 3. 27 на 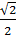 получим
получим
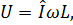 откуда получим формулу
откуда получим формулу
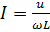 3. 28
3. 28
Закона Ома для действующих значений тока и напряжения в цепи с индуктивностью.
Величина, стоящая в знаменателе, имеет характер в размерность сопротивления и называется индуктивным сопротивлением или реактивным сопротивлением индуктивности
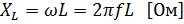 3. 29
3. 29
Индуктивное сопротивление прямо пропорционально частоте переменного тока и индуктивности цепи и характеризует влияние ЭДС самоиндукции на величину тока.
Для цепи с индуктивностью закон Ома справедлив только для амплитудных и действующих значений тока и напряжения. Для мгновенных значений в этом случаем закон Ома неприменим, так как
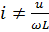
Мгновенное значение мощности в цепи с индуктивностью равно произведению мгновенных значений напряжения тока
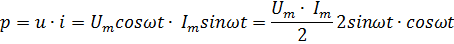
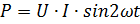 3. 30
3. 30
Следовательно, мгновенное значение мощности в цепи с индуктивностью измеряется по синусоидальному закону с двойной частотой. На рис. 67 представлен график изменения мощности за период. Из графика видно, что в течение первой четверти периода ток в цепи нарастает. При этом возрастает энергия магнитного поля, т.е. энергия поступает от генератора в катушку. Во вторую четверть периода ток в цепи уменьшается, уменьшается по величие и магнитное поле катушки.
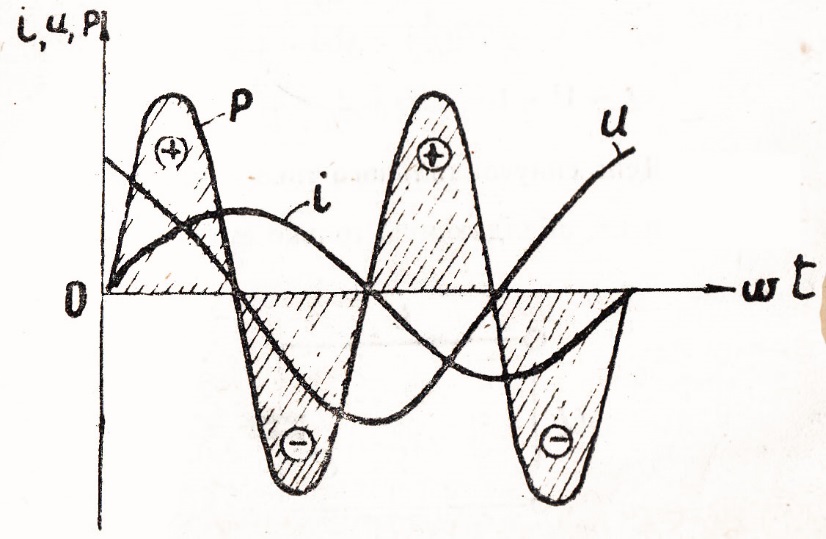
Рис. 67
При этом энергия магнитного поля превращается в электрическую и возвращается обратно в генератор. Аналогичные процессы происходят в течение второго полупериода.
Таким образом, энергия, полученная цепью за каждую половину периода равна нулю, следовательно, равна нулю и средняя мощность цепи
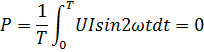
В цепи с индуктивностью происходит периодический обмен энергией между генератором и магнитным полем катушки без необратимого преобразования электрической энергии. Колебания энергии характеризуются реактивной мощностью, которая равна амплитудному значению мгновенной мощности
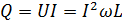
Реактивная мощность измеряется в вольтметрах реактивных(Вар).
Пример 16. Катушка с индуктивностью L=43,8 мГн включена в цепь синусоидального тока с напряжением U=220 В. Определить ток в цепи и реактивную мощность. Частота переменного тока f=400 Гц.
Решение:
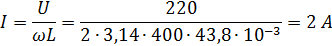
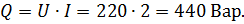
Дата добавления: 2016-04-06; просмотров: 6088;
