Индуктивность в цепи синусоидального тока. Из опыта известно, что для контуров (катушек) с неферромагнитным сердечником или для катушек с сердечником из магнитодиэлектриков

Из опыта известно, что для контуров (катушек) с неферромагнитным сердечником или для катушек с сердечником из магнитодиэлектриков, у которых магнитная проницаемость µ почти постоянная и не зависит от напряжённости магнитного поля, потокосцепление ψ пропорционально току :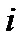

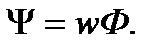(2-29)

Коэффициент пропорциональности L называют собственной индуктивностью контура или индуктивностью.

[L]= 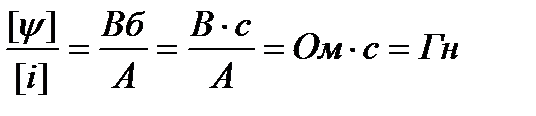(Генри).

Практически любая катушка обладает некоторой индуктивностью L и активным сопротивлением R. На схеме катушку можно представить в виде последовательно соединённых индуктивностей L и резистора с сопротивлением R. Выделим из схемы одну индуктивность (рис.13).

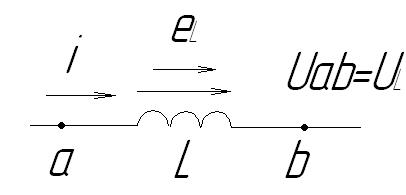
Рис. 2-13. Катушка индуктивности в цепи синусоидального тока

Через индуктивность L течёт синусоидальный ток . В катушке находится ЭДС самоиндукции.

(2-30)

Положительное направление отсчёта для ЭДС 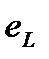обозначено стрелкой, совпадающей с положительным направлением отсчёта тока (рис. 2-13).

Найдём разность потенциалов между точками “a” и “b”. При перемещении от точки “b” к точке “a” идём навстречу ЭДС 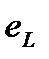, поэтому 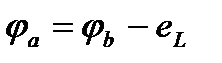, следовательно:

Таким образом, напряжение на катушке индуктивности 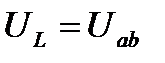противоположно ЭДС самоиндукции :

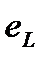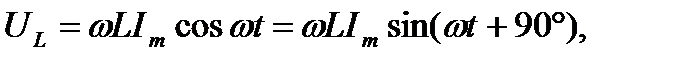(2-31)

здесь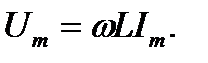

Из закона Ома ясно, что ωt это некоторое сопротивление.

Произведение ωL обозначают и называют индуктивным сопротивлением.

(2-32)

Проверим его размерность:

Таким образом, индуктивность оказывает переменному току сопротивление 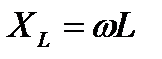. Оно прямо пропорционально частоте.

Изобразим на векторной диаграмме комплексы действующих значений тока , напряжения на катушке 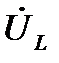и ЭДС самоиндукции 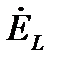(рис. 2-14).

Рис. 2-14. Векторная диаграмма

У тока 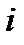нулевая начальная фаза, поэтому комплекс действующего значения отложен по вещественной оси.

У напряжения на катушке фаза равна 90º. Положительные углы на комплексной плоскости откладываются от вещественной оси против часовой стрелки. Поэтому комплекс действующего значения напряжения на катушке 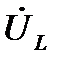направлен помнимой оси.

У ЭДС самоиндукции 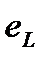фаза равна минус 90º. Отрицательные углы на комплексной плоскости откладываются по часовой стрелке. Поэтому комплекс действующего значения ЭДС самоиндукции 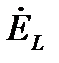отложен вдоль отрицательного направления мнимой оси.

Таким образом, при протекании синусоидального тока через катушку индуктивности вектор тока отстаёт от вектора напряжения на катушке на 90º.

Найдём теперь мгновенную мощность p для данного случая:

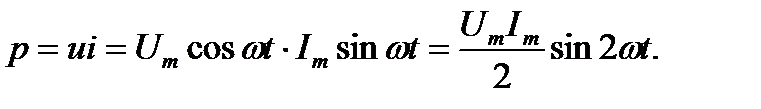(2-33)

Изобразим на временной диаграмме графики тока i, напряжения 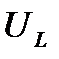и мгновенной мощности p (рис. 2-15).

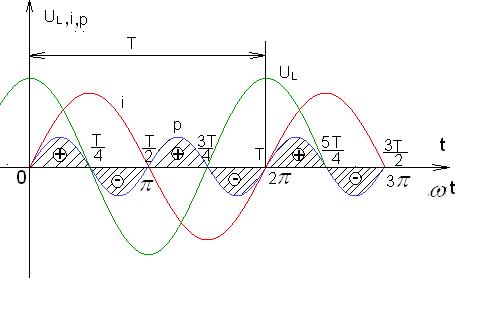
Рис. 2-15. Графики мгновенных значений тока i, напряжения и мощности р.

Мгновенная мощность p положительная в первую, третью и все нечетные четверти периода, когда напряжение 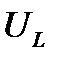и ток 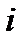имеют одинаковые знаки. Площадь, ограниченная кривой р и осью абсцисс за четверть периода, представляет собой энергию, которая взята от источника питания на создание магнитного поля в катушке индуктивности.

Мгновенная мощность р отрицательная во вторую, четвёртую и все четные четверти периода, когда напряжение и ток имеют разные знаки. Во вторую, четвёртую и все чётные четверти периода, когда ток в цепи уменьшается от максимума до нуля, энергия, запасённая в магнитном поле катушки индуктивности, возвращается обратно источнику. Направление потока энергии меняется на противоположное.

Таким образом, в катушке индуктивности не происходит потребление энергии от источника, а происходит накапливание энергии в магнитном поле катушки индуктивности в нечётные четверти периода и возврат накопленной энергии источнику во все чётные четверти периода.

Напомним, что элемент, не потребляющий энергию от источника, называется реактивным и обладает реактивным сопротивлением. То есть катушка индуктивности – это реактивный элемент, обладающий реактивным сопротивлением .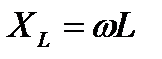

Мгновенная мощность р принимает нулевое значение каждую четверть периода, когда либо ток 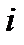, либо напряжение 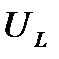равны нулю.