Конденсатор в цепи синусоидального тока
Если приложенное к конденсатору напряжение не меняется во времени, то заряд q=CU на одной его обкладке и заряд –q=-Cu на другой (С-ёмкость конденсатора) неизменны и ток через конденсатор не проходит ( 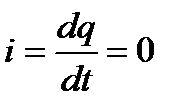 ). Если же напряжение на конденсаторе меняется во времени, например по синусоидальному закону
). Если же напряжение на конденсаторе меняется во времени, например по синусоидальному закону
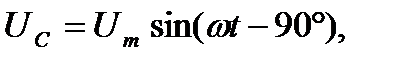 (2-34)
(2-34)
то по синусоидальному закону будет меняться заряд q конденсатора:
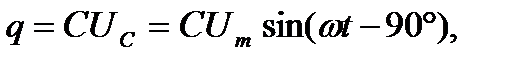 (2-35)
(2-35)
и конденсатор будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него синусоидального тока
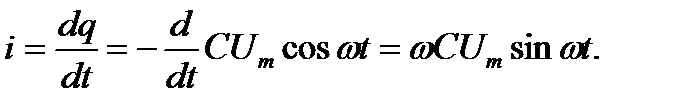 (2-36)
(2-36)
Из сопоставления (2-34) и (2-36) видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90º. На векторной диаграмме вектор тока 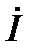 направлен по вещественной оси комплексной плоскости, а вектор напряжения на конденсаторе направлен в отрицательном направлении мнимой оси.
направлен по вещественной оси комплексной плоскости, а вектор напряжения на конденсаторе направлен в отрицательном направлении мнимой оси.
На рис. 2-16 изображен конденсатор емкостью С, по которому протекает синусоидальный ток 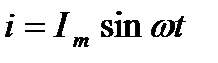 .
.
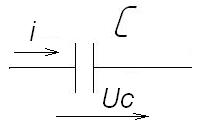
Рис. 2-16. Конденсатор в цепи синусоидального тока
На рис. 2-17 изображена векторная диаграмма при протекании через конденсатор синусоидального тока.
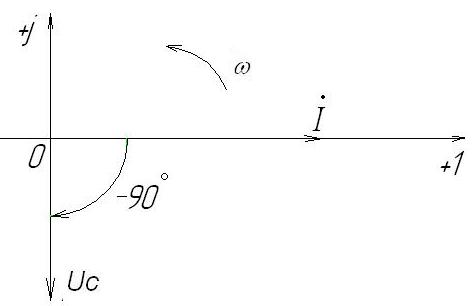
Рис. 2-17. Векторная диаграмма
Таким образом, при протекании синусоидального тока через конденсатор вектор тока 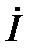 опережает вектор напряжения на конденсаторе
опережает вектор напряжения на конденсаторе 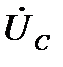 на 90º.
на 90º.
Из выражения (2-36) запишем амплитуду тока 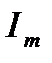 :
:
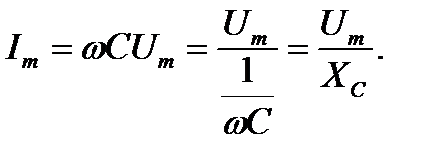 (2-37)
(2-37)
Ясно, что выражение в знаменателе есть некоторое сопротивлению согласно закону Ома:
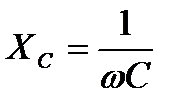 , (2-38)
, (2-38)
которое называют емкостным сопротивлением конденсатора.
Проверим размерность Xc:
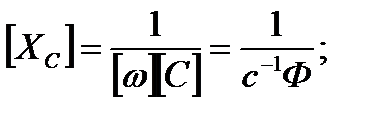
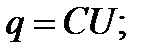
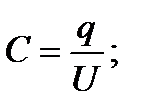
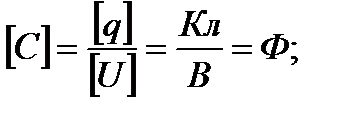
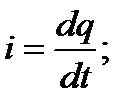
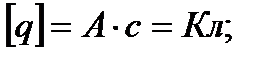
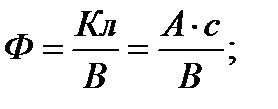
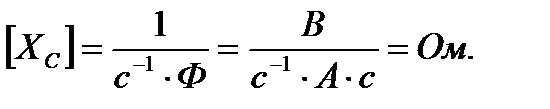 (2-39)
(2-39)
Таким образом, конденсатор оказывает переменному току сопротивление 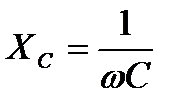 . Оно обратно пропорционально угловой частоте ω.
. Оно обратно пропорционально угловой частоте ω.
Мгновенная мощность.
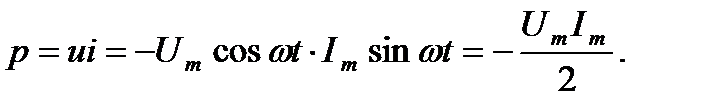 (2-40)
(2-40)
Графики мгновенных значений U,I,p приведены на рис. 2-18.
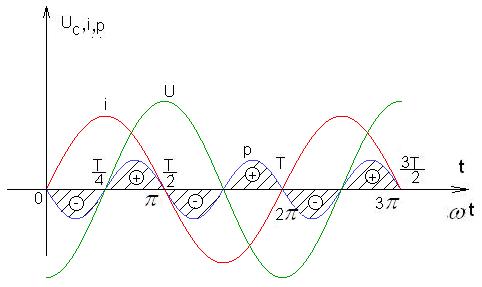
Рис. 2-18. Графики мгновенных значений тока 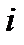 , напряжения
, напряжения 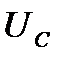 и
и
мощности p
Во вторую и все чётные четверти периода мгновенная мощность р положительная, и в этой четверти периода энергия от источника передаётся конденсатору и идёт на создание электрического поля конденсатора.
В первую и все нечётные четверти периода мгновенная мощность р отрицательная, и энергия, занесённая в электрическое поле конденсатора, возвращается источнику.
Мгновенная мощность положительная, когда напряжение 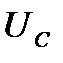 и ток
и ток 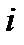 имеют одинаковые знаки, и отрицательная – когда напряжение
имеют одинаковые знаки, и отрицательная – когда напряжение 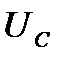 и ток
и ток 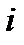 имеют противоположные знаки.
имеют противоположные знаки.
Мгновенная мощность р равна нулю, когда либо ток 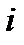 , либо напряжение
, либо напряжение 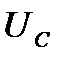 проходят через нуль. Это происходит каждую четверть, поэтому мгновенная мощность изменяется с двойной частотой питающей сети.
проходят через нуль. Это происходит каждую четверть, поэтому мгновенная мощность изменяется с двойной частотой питающей сети.
Таким образом, в конденсаторе не происходит потребление энергии от источника, а происходит накапливание энергии в электрическом поле конденсатора в чётные четверти периода и возврат накопленной энергии источнику в нечётные четверти периода.
Напомним, что элемент, не потребляющий энергию от источника, называется реактивным и обладает реактивным сопротивлением. То есть конденсатор – это тоже реактивный элемент, обладающий реактивным сопротивлением 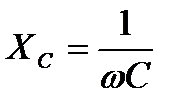 .
.
Диэлектрик, находящийся между обкладками конденсатора, всегда неидеален, то есть в нем всегда есть некоторые потери энергии, которые относительно малы и ими часто можно пренебречь. Если требуется учесть их в расчёте , то конденсатор заменяют схемой замещения (рис. 2-19), в которой параллельно ёмкости присоединено активное сопротивление R, потери энергии в котором имитируют потери энергии в реальном диэлектрике.
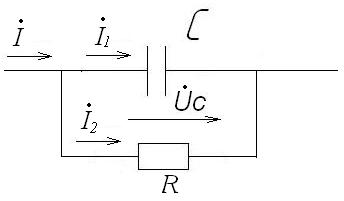
Рис. 2-19. Схема замещения реального конденсатора
На рис. 2-20 приведена векторная диаграмма для реального конденсатора.
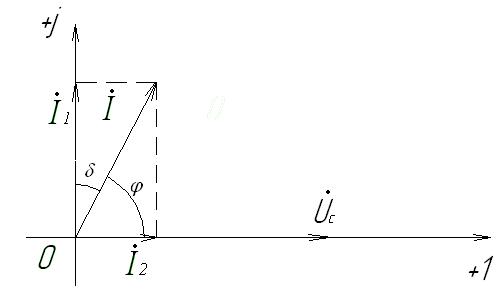
Рис. 2-20. Векторная диаграмма реального конденсатора
На диаграмме вектор напряжения на конденсаторе 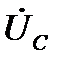 направлен по вещественной оси комплексной плоскости. Вектор тока
направлен по вещественной оси комплексной плоскости. Вектор тока 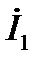 через конденсатор опережает вектор напряжения
через конденсатор опережает вектор напряжения 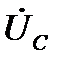 на 90º, то есть направлен в положительном направлении мнимой оси. Вектор тока
на 90º, то есть направлен в положительном направлении мнимой оси. Вектор тока 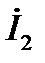 через сопротивление R совпадает по направлению
через сопротивление R совпадает по направлению 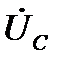 , то есть направлен по вещественной оси. Ток
, то есть направлен по вещественной оси. Ток 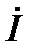 через реальный конденсатор равен согласно первому закону Кирхгофа:
через реальный конденсатор равен согласно первому закону Кирхгофа:
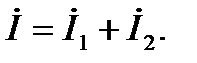 (2-41)
(2-41)
В результате ток 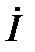 реального конденсатора опережает
реального конденсатора опережает 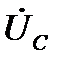 на угол
на угол 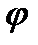 меньший 90º. Угол
меньший 90º. Угол 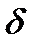 между токами
между токами 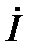 и
и 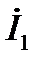 называют углом потерь, он зависит от сорта диэлектрика и частоты. В справочниках обычно приводят
называют углом потерь, он зависит от сорта диэлектрика и частоты. В справочниках обычно приводят 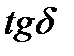 или обратную величину
или обратную величину
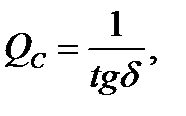 (2-42)
(2-42)
которую называют добротностью контура.
Чем лучше диэлектрик, то есть чем меньше в нём потери энергии, тем меньше угол 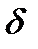 и тем больше добротность конденсатора
и тем больше добротность конденсатора 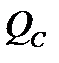 .
.
Дата добавления: 2016-03-15; просмотров: 4627;
