Занятие 3. Электроёмкость, конденсаторы, энергия электростатического поля

Задача 2

Определить A'работу внешней силы по увеличению расстояния между обкладками

от y₁до y₂значенийв воздушном плоском конденсаторе с S площадью обкладок в первом случае при неизменном q заряде на обкладках, а во втором случае при неизменномU напряжении между этими обкладками. Дано: z₁; z₂; S; 1) q = const; 2) U = const/A'|_q_{= const} = ? A'| _U=_const = ?

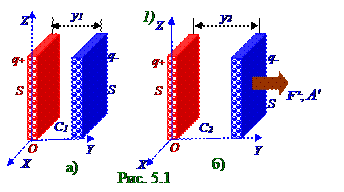
В первомслучае (рис. 5.2.7) A'работа внешней силы, которая в (1.109) из раздела 1.0 "Физические основы механики"называется работойA_стсторонней силы, приводит к приращению ΔW_p потенциальнойэнергии, т.е. в случае с электрическим конденсатором приводит (5.149) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического

поля"к следующемуприращению ΔW электрической энергии плоского конденсатора:

A' = ΔW = (q²/2C₂) - (q²/2C₁) = (q²ε₀S/2)(y₂- y₁), (4.1)где (5.125) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля" C₁= ε₀S/y₁- ёмкость (рис.5.1, а) воздушного конденсатора с S площадью обкладок и с y₁расстоянием между этими обкладками; C₂= ε₀S/y₂- ёмкость (рис.5.1, б) воздушного конденсатора с S площадью обкладок и с y₂расстоянием между этими обкладками.

Во второмслучае (рис.5.2) кроме A'работы внешней силы, которая в (1.108) из раздела 1.0 "Физические основы механики"называется работойA_стсторонней силы, существует (рис. 6.1) из раздела 6.0 "Электрический ток" A_эработа ε_э электродвижущей силы (ЭДС), которая создаёт неизменноеU напряжение между обкладками конденсатора. Приращение ΔW электрической энергии плоского конденсатораопределяется суммойA'работы внешней силы и A_эработы ε_э ЭДС:

Обкладки конденсатора по (5.1) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля"закону Кулона притягиваются друг к другу, поэтому для увеличения y расстояния между этими обкладками следует приложить вектор F' внешней силы, совпадающий по направлению с вектором перемещения, т.е. (1.82) из раздела 1.0 "Физические основы механики"α угол между вектором F' внешней силы и векторомперемещения равен нулю, поэтому A'работа этого вектора F' внешней силы больше нуля, т.е. A' > 0.

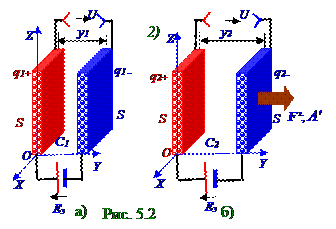
внешней силы и A_эработы ε_э ЭДС:

A' + A_э = ΔW ↔ A' + ΔqU = ΔW ↔ A' + (q₂- q₁)U = (q₂²/2C₂) - (q₁²/2C₁) ↔ A' + (UC₂- UC₁)U =

= (q₂²/2C₂) - (q₁²/2C₁) ↔ A' + (UC₂- UC₁)U = (U²C₂²/2C₂) - (U²C₁²/2C₁) ↔ A' + [(Uε₀S/y₂) - (Uε₀S/y₁)]U =

= (U²ε₀S/2y₂) - (U²ε₀S/2y₁) ↔ A' = (U²ε₀S/2)(y₂ - y₁)/2y₂y₁,(4.2)

где Δq = q₂- q₁= (UC₂) - (UC₁) = (Uε₀S/y₂) - (Uε₀S/y₁) < 0 - приращение заряда на каждой из обкладок

S площадью воздушного конденсатора при увеличении расстояния между этими обкладками от (рис. 5.1, а) y₁до (рис. 5.2.7, б) y₂значений, что приводит к уменьшениюёмкости от C₁= ε₀S/y₁до C₂= ε₀S/y₂и вследствие этого при постоянномU напряжении между обкладками происходит уменьшениезаряда на каждой из обкладок от q₁ = UC₁= Uε₀S/y₁до q₂ = UC₂= Uε₀S/y₂ значений;и вследствие этого при постоянномU напряжении между обкладками происходит уменьшениезаряда на каждой из обкладок от q₁ = UC₁= Uε₀S/y₁до q₂ = UC₂= Uε₀S/y₂ значений; A_э= ΔqU = (q₂- q₁)U = (U²C₂) - (U²C₁) = (U²ε₀S/y₂) - (U²ε₀S/y₁) < 0 - отрицательное значение работы (6.33) из раздела 6.0 "Электрический ток", совершаемой сторонними силами, вследствие наличия в этой цепи постоянного электрического тока источника ЭДС ε_э величиной, по перемещению величины Δq заряда от 1-ой ко 2-ой обкладке, т.е. навстречу направлению ЭДС, вследствие чего эта A_эработы ε_э ЭДС является отрицательной.

Во второмслучае, как и в первомслучае, A'работа (рис.5.2.8) вектора F' внешней силы по увеличению y расстояния между обкладками больше нуля, т.е. A' > 0.

Задача 2

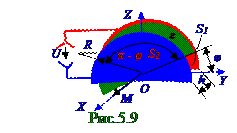
В конденсатор c постоянным U напряжением, c h расстоянием между плоскими неподвижными полукруглыми обкладками R радиуса поместили подвижную полукруглую пластину h толщинойс ε диэлектрической проницаемостью. Эту полукруглую диэлектрическую пластину вращают без трения против "часовой стрелки". Найти M модуль и направление вектора M момента силы, который действует со стороны электрического

поля на подвижную полукруглую пластину, при её повороте относительноOX оси от положения, совпадающем с неподвижными полукруглыми обкладками, до положения, когда подвижная полукруглая пластина повернётcя на φ угол. Дано: ε; h; U; R /A'| M = ? M = ?

Площадь S₁ обкладок, имеющих форму двух секторов в круге R радиусом с φ центральным углом, воздушного плоского конденсатора имеет следующий вид: S₁= φπR²/2π = φR²/2.(5.1) Площадь S₂ обкладок, имеющих форму двух секторов в круге R радиусом с

π - φ центральным углом, плоского конденсатора имеет следующий вид: S₂= (π - φ)πR²/2π = φR²/2.(5.2) Емкость C₁ воздушного плоского конденсатора, имеющего (5.1) площадь S₁ обкладок и

h расстояние между ними, имеет следующий вид: C₁= ε₀S₁/h = ε₀αR²/2h.(5.3) Емкость C₂ плоского конденсатора, имеющего (5.2) площадь S₂обкладок, которое заполнено полукруглой пластиной h толщинойс ε диэлектрической проницаемостью, имеет следующий вид: C₂= ε₀εS₂/h = ε₀ε(π - φ)R²/2h. (5.4) Общая C₀емкость плоского конденсатора, имеющего (5.2) емкость C₁ воздушного плоского конденсатора с подключенным параллельноему плоским конденсатором с полукруглой пластиной

h толщиной, ε диэлектрической проницаемостью и (5.4) C₂ емкостью, имеет следующий вид:

C₀= C₁+ C₂= (ε₀R²/2h)[φ + ε(π - φ)]. (5.5) Электрическая энергия (5.149) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля" с учётом (5.5) общей

C₀емкости плоского конденсатора, когда (рис.5.9) подвижная полукруглая диэлектрическая пластина повёрнута на α угол, имеет следующий вид: W_e = U²C₀/2 = (ε₀U²R²/4h)[φ + ε(π - φ)]. (5.6) Элементарное приращение dW_e электрической энергии плоского конденсатора c постоянным

U напряжением при положительном элементарном приращении dφ угла, т.е. повороте полукруглой пластины h толщиной, ε диэлектрической проницаемостью против "часовой стрелки" на этот dφ угол, имеет следующий вид: dW_e = (∂W_e/∂φ)dφ =(ε₀U²R²/4h)(1 - ε)dφ = - (ε₀U²R²/4h)( ε - 1)dφ < 0, (5.7) т.к. ε диэлектрическая проницаемость пластины h толщиной больше нуля, т.е. ε > 0.

Элементарное приращение dW_e электрической энергии плоского конденсатора c постоянным

U напряжением при положительном элементарном приращении dφ угла, т.е. повороте относительно

OX оси полукруглой пластины h толщиной, ε диэлектрической проницаемостью против "часовой стрелки" на этот dφ угол, согласно (5.7) отрицательно. Поэтому (1.91) из раздела 1.0 "Физические основы механики"элементарная δA' работа, выполненная вектором M моментавнешних сил, при повороте относительно OX оси полукруглой пластины h толщиной, ε диэлектрической проницаемостью против "часовой стрелки" на вектор dφ бесконечно малого угла равна (5.7) элементарному приращению dW_e электрической энергии плоского конденсатора, вследствие чего имеет место следующее выражение: δA' = dW_e ↔ δA' =M'dφ= M'_OX dφ =- (ε₀U²R²/4h)( ε - 1)dφ < 0 ↔

↔ M'_OX =- (ε₀U²R²/4h)(ε - 1).(5.8) Согласно (5.8) вектор M'моментавнешних сил имеет (рис. 5.9) отрицательную M'_OXпроекциюнаOX ось, т.е. этот вектор M'моментавнешних сил направлен противоположно направлению OX оси и противоположно вектору dφ бесконечно малого угла поворота полукруглой пластины h толщиной, ε диэлектрической проницаемостью, направленного по OX оси.

Поэтому вектор M'моментавнешних сил равен помодулю и противоположен по направлению (рис. 05.2.9) вектору M момента силы со стороны электрического поля, который направлен по

OX оси, т.е. вращает полукруглую пластину h толщиной, ε диэлектрической проницаемостью против "часовой стрелки".

Модуль M вектору M момента силы со стороны электрического поля с учётом (5.8) имеет следующий вид: M =(ε₀U²R²/4h)(ε - 1),(5.9)

т.е. вращающий момент сил, втягивающий полукруглую пластину не зависит от φ угла поворота относительно положения, совпадающем с неподвижными полукруглыми обкладками, а прямо пропорционален ε диэлектрической проницаемости, квадратам R²радиусов и постоянного

U² напряжения между обкладками и обратно пропорционален h толщине этой полукруглой пластины.

<== предыдущая лекция	\|	следующая лекция ==>
Cвободные, т.е.нескомпенсированные,заряды равномерно распределены с объёмной	\|	Электрический ток. Природа носителей тока в металлах

Дата добавления: 2016-02-14; просмотров: 1124;