Электрический ток. Природа носителей тока в металлах

Если через некоторую воображаемуюповерхность переносится суммарныйзаряд, отличный от нуля, то говорят, что через эту воображаемуюповерхность течёт электрический ток. Электрический ток может течьв твёрдых телах таких, как металлы, полупроводники, в проводящих жидкостях, которые называют электролитами. В газах электрический ток течётв результате газового разряда.

Для протекания электрического токанеобходимо наличие в данной среде заряженных частиц, которые могут перемещаться в пределах этой среды и которые называются носителями тока. Носителями электрического токамогут быть электронылибо ионы, либо макроскопические частицы, несущие на себе избыточныйзаряд, например, заряженные пылинкии капельки.

Электрический ток возникает при условии, что внутри проводящей средысуществует электрическоеполе. Носители электрического токапри отсутствии электрическогополя принимают участие в тепловом молекулярномдвижении с (4. 240) из раздела 4.2 "Физическая термодинамика"векторомv_i скорости, который в пространстве скоростей (рис.4.25) из раздела 04.2.0 "Физическая термодинамика" имеет любое направлениев прямоугольной декартовой (рис.1.1) из раздела 1.0 "Физические основы механики"системе координат. При отсутствии электрическогополя произвольную воображаемуюповерхность в проводящей средепересекают за интервал Δt времени одинаковое количество положительныхи отрицательных носителей электрического тока. Поэтому электрический токв проводящейсреде при отсутствии электрическогополя равен нулю.

При включении электрическогополя помимо теплового молекулярногодвижения с векторомv_i скоростиносители электрического токадвигаютсяупорядоченно по направлению этогоэлектрическогополя с векторомu_i скорости. Таким образом, результирующий вектор скоростиносителей электрического токав данный момент t времени будет равен v_i + u_i.Среднее(4.39) из раздела 04.1.0 "Физическая термодинамика"значение вектора <v_i >теплового молекулярного движенияносителей электрического токаравно нулю, т.к. в движениепо любому направлению вектораv_i скорости этихносителей электрического токав положительнуюи отрицательнуюстороны равновероятны.Поэтому среднее значение результирующего вектора <v_i + u_i > скороститеплового молекулярногои упорядоченного движенияносителей электрического токапри наличии в проводящейсреде электрическогополя равно следующему среднему значению вектора <u_i > скорости движения носителей электрического токапо направлению вектора E напряжённости этого электрическогополя: <v_i + u_i > = <v_i > + <u_i > = <u_i >. (6.1)

Количественной характеристикой электрического токаслужит величина Δq заряда, переносимого через воображаемуюповерхность S площадью в проводящей среде носителями электрического токав единицу t времени. Если за элементарный dt промежуток времени через воображаемуюповерхность S площадью переносится носителями электрического токаэлементарный dqзаряд, то сила I тока имеет следующий вид: I = dq/dt. (6.2)

Если за равные промежутки Δt времени через воображаемуюповерхность S площадью переносится носителями электрического токаодна и та же величина Δq заряда, т.е. dq/dt = const в выражении (6.2), то через эту воображаемуюповерхность S площадью течёт следующий токспостояннойI_псилой: I_п = Δq/Δt. (6.3) Электрический ток может быть обусловлен движением как положительных, так и отрицательных носителей электрического тока. Перенос отрицательногоq_- заряда в одном направлении эквивалентен переносу такого же по величине положительного q₊ заряда в противоположном направлении. Перенос положительного q₊ заряда в одном направлении эквивалентен переносу такого же по величине отрицательногоq_- заряда в противоположном направлении.

Если электрическийток создаётся носителямиобоих знаков, причём за элементарный dt промежуток времени в проводящей среде через воображаемуюповерхность S площадью положительныеносители переносят элементарный dq₊ заряд в одном направлении, а отрицательныеносители за тот же элементарный dt промежуток времени в проводящей среде через ту же воображаемуюповерхность S площадью переносят элементарный dq_- заряд в противоположном направлении, то сила I тока имеет следующий вид: I = (dq₊/dt) + (|dq_-|/dt). (6.4)

где |dq_-| = - dq_- - модуль отрицательногоэлементарного заряда.

где j - векторплотности электрическоготока в точках элементарнойповерхности dS площади; n - единичный вектор, нормальный к элементарнойповерхности dS площадью; dS = dSn- векторэлементарнойповерхности dS площадью; j_n = jcos(j,^n) - проекция вектора j плотности электрическоготока в точках элементарнойповерхности dS площади на направление единичного n вектора нормали к этой элементарнойповерхности dS площадью; dS_┴ = dScos(j,^n) - площадь проекции элементарнойповерхности dS площадьювоображаемойповерхности S площадью на плоскость, перпендикулярную вектору j плотности электрическоготока; j - модуль вектора j плотности электрическоготока в точках элементарнойповерхности dS площадью.

Вектор j плотности электрическоготока коллинеарен и направлен в одну сторону с вектором <u_i > скорости движения положительных носителей электрического тока.

По аналогии (5.16) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля"с потоком N_E вектора E напряженностив вакууме электростатическогополя сила I тока сквозь воображаемуюповерхность S площадью в проводящей среде равен следующему интегралуот элементарных величин dI силы тока сквозь все элементарные поверхности dS площадью этой воображаемойповерхности S площадью:

I = ∫dI = ∫jdS = ∫jdScos(j^n) = ∫j_ndS = ∫jdS_┴. (6.6) S S S S S

Элементарная классическая теория проводимости металлов

Если электрическийток создаётся (6.4) носителямиобоих знаков, то за единицу t времени через (рис. 6.1) поверхность единичной площади, перпендикулярную вектору j плотности электрическоготока, выражение для модуля j этого вектора j плотности электрическоготока имеет следующий вид: j= q₊ n₊u₊ + |q_-|n_-u_- ↔ j= ρ₊u₊ + ρ_-u_-,(6.7)

где q₊, n₊, u₊ и q_-, n_-, u_- -соответственно величина заряда, концентрация и (6.1) модули среднего значения векторов <u_i > скорости движенияположительныхиотрицательных носителей электрического тока; ρ₊ = q₊ n₊ и ρ_-= |q_-|n_- -объёмные плотности соответственноположительныхиотрицательных носителей электрического тока, т.е. количество положительногоиотрицательногозарядав единицеобъёма в проводящей среде, где протекает электрический ток.

Уравнение непрерывности электрического тока в интегральном и дифференциальном видах в области с зарядами

При убывании в зависимости от t времени величины q заряда носители электрического токас вектором j плотностиэтого электрическоготока покидают (рис.6.2) область V объёма,

ограниченную замкнутой поверхностью S площадью,где (6.2) dq/dt<0, т.е эта область V объёма является "истоком"зарядов.

При возрастании в зависимости от t времени величины q заряда носители электрического токас вектором j плотностиэтого электрическоготока накапливаются (рис.6.3) в области V объёма,

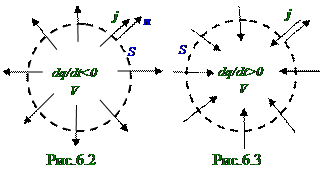
области, ограниченной замкнутой поверхностью S площадью; q = |q_-| -в случае отрицательногозаряда в области, ограниченной замкнутой поверхностью S площадью; знак "-"перед dq/dt учитывает, что в случае убывания в зависимости от t времени величины qзаряда, т.е. dq/dt<0, вектор j плотности электрическоготока направлен по направлению внешней n нормали к замкнутой поверхности

S площадью, т.е. вектор j плотности электрическоготока направлен в положительную сторону; в случае возрастания в зависимости от t времени величины qзаряда, т.е. dq/dt>0, вектор j плотности электрическоготока направлен против направления внешней n нормали к замкнутой поверхности

S площадью, т.е. вектор j плотности электрическоготока направлен в отрицательную сторону.

В случае непрерывнораспределенногоq заряда с известной (5.10) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" объёмнойρ = dq/dV плотностью величина q заряда (рис.6.2), (рис.6.3) в V объёме, ограниченном замкнутой поверхностью S площадью, определится следующим интегрированием объёмнойρплотности зарядов по V объёму: q = ∫ρdV.(6.9) V

Подставляем (6.9) в (6.8) и получаем следующее выражение уравнениянепрерывностив интегральномвиде для электрического тока, согласно которому сила I тока сквозь воображаемуюзамкнутую поверхность S площадью в проводящейсредеравняетсяскорости изменения во t времени q заряда в V объёме, ограниченном этой замкнутой поверхностью S площадью:

I = ∫jdS = - d/dt( ∫ρdV) = - ∫(∂ρ/∂t)dV,(6.10) (S) V V

где ∂ρ/∂t -частная первая производная по t времени от объёмнойρ плотностизарядов введена потому, что объёмнаяρ плотностьзарядов может зависеть также от координат пространства, где находится этот заряд.

Заменив в (6.10) поверхностныйинтегралпозамкнутойповерхности S площадью объёмным интегралом по V объёму, ограниченному этой замкнутойповерхностью S площадью, получим следующее выражение уравнениянепрерывностив дифференциальномвиде для электрического тока, протекающего в проводящейсреде: ∫jdS= ∫ jdV = - ∫(∂ρ/∂t)dV ↔ j =- ∂ρ/∂t ↔ (S) V V

↔ j = [(∂/∂x)i + (∂/∂y)j + (∂/∂z)k]j = (∂j_x/∂x) + (∂j_y/∂y) + (∂j_z/∂z) = - ∂ρ/∂t, (6.11) Согласно (6.11) по аналогии с (5.21) из раздела 5.1 "Электростатика"уравнениенепрерывностив дифференциальномвиде для электрического тока, протекающего в проводящейсреде, имеет следующую формулировку: дивергенцияdivj = j вектораj плотности электрическоготока численно равнасумме приращенийпроекций j _x; j _y и j _z на оси OX, OY и OZ координат вектора

j плотностиэтого электрическоготока по каждой из OX, OY и OZ осей координат на единицеих длиныв рассматриваемой точке некоторого объёма. Этоприращениепроекцийj _x; j _y и j _z вектора

j плотности электрическоготока, протекающего в проводящейсреде, равна взятой с противоположным знаком скорости изменения по t времени объёмнойρ плотностизарядов, находящихся в рассматриваемой точке проводящейсреды.

Уравнение непрерывности электрического тока в интегральном и дифференциальном видах в области, в которой отсутствуют источники и стоки зарядов

Входящий(рис.6.4)ток в пределах малойΔS₁ площадки I₁ = j₁ΔS₁ силой в проводящейсреде, имеющийв пределах этой малойΔS₁ площадки вектор j₁ плотности электрическоготока, вследствие неразрывностилиний электрическоготока, которые на рис.6.4 изображены штрих - пунктирными зелёнымилиниями, равен по модулю и противоположен по знаку выходящемутоку

I₁' = j 'ΔS_i', имеющемув пределах малойΔS₁' площадки векторj₁' плотности электрическоготока.

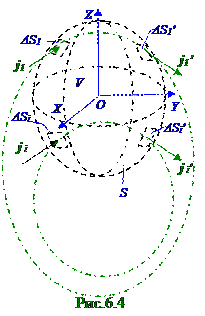
Выражение (6.12) является по аналогии с (7.19) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" математическимвыражением уравнениянепрерывностив интегральномвиде для постоянного электрического тока в V объёмепроводящейсреде, ограниченной воображаемой замкнутойповерхности S площадью, когда в этом V объёме отсутствуют (рис. 06.0.2) источникиили (рис.6.3) стоки носителей электрическоготока, т.е. когда количество входящих носителей электрическоготокав V объёмепроводящейсреды равно количеству выходящих носителей электрическоготокавэтот V объёмпроводящейсреды.

Заменив в (6.12) поверхностныйинтегралпозамкнутойповерхности S площадью объёмным интегралом по V объёму, ограниченному этой замкнутойповерхностью S площадью, получим следующее выражение уравнениянепрерывностив дифференциальномвиде для постоянного электрического тока, протекающего в проводящейсреде: ∫jdS= ∫ jdV = 0 ↔ j =0 ↔

(S) V

↔j = [(∂/∂x)i + (∂/∂y)j + (∂/∂z)k]j = 0 ↔j = (∂j_x/∂x) + (∂j_y/∂y) + (∂j_z/∂z) = 0, (6.13)

Согласно (6.13) по аналогии с (7.20) из раздела 07.1.0 "Магнитостатика"уравнениенепрерывностив дифференциальномвиде для постоянного электрического тока, протекающего в проводящейсреде, имеет следующую формулировку: дивергенцияdivj = j вектора j плотности постоянного электрическоготокаравно нулю, т.е. численное значение суммы приращений проекций

j _x; j _y и j _z вектора j плотностиэтого электрическоготока по каждой из OX, OY и OZ осей координат на единицуих длиныв рассматриваемой точке в V объёмепроводящейсреды, где отсутствуют

(рис.6.2) источникиили (рис. 06.0.3) стоки носителей электрическоготока, равна нулю.

Закон Ома для однородного участка цепи в интегральном и дифференциальном видах

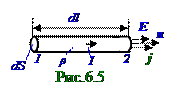
(5.15) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля"равняется модулюE вектораE напряжённости электростатического поля.

Разность потенциаловφ₁ - φ₂ между 1-ой и 2-ойсторонамипроводника по аналогии с (5.117) из раздела 5.2 "Электростатика"с учётом постоянного значения проекции E_n на n нормаль к элементарной dS площади поперечного сечения проводникавектораE напряжённости электрического поля на элементарной dl длине проводника имеет следующий вид: φ₁ - φ₂ = E_ndl= Edl.(6.14) Участок 1- 2 электрической цепи (рис.6.5) является однородным, т.к. на нём отсутствует ЭДС. Поэтому (6.15) U₁₂ напряжениемежду левой и правой стороной проводника равно разности φ₁ - φ₂ потенциалов в электрической цепи между 1-ой и 2-ойсторонамипроводника, вследствие чегодляэтогоU₁₂ напряженияимеет место следующее выражение: U₁₂ = φ₁ - φ₂. (6.15) Сила I тока (рис.6.5) в проводнике с учётом выражения (6.6) имеет следующий вид: I = j_ndS = jdS, (6.16) где проекция j_n на n нормаль к элементарнойповерхности dS площадью поперечного сечения проводника вектора j плотности электрическоготока равняется модулю j этого вектора j плотности электрическоготока, поскольку вектор j плотности электрическоготока направлен по

n нормали к элементарнойповерхности dS площадью поперечного сечения

проводника.

По закону Ома для однородного участка цепив интегральном виде сила I тока (рис.6.5) между левой и правой стороной проводника с учётом выражения (6.15) имеет следующий вид: I = U₁₂/R ↔ I = φ₁ - φ₂/R. (6.17) Сопротивление R проводника с элементарными dl, dS соответственно длиной, площадью поперечного сечения и удельным ρ_с объёмным сопротивлением проводящего материала этого проводника имеет следующий вид: R = ρ_сdl/dS. (6.18)

Подставляем в (6.17) разность(6.14) потенциаловφ₁ - φ₂ между 1-ой и 2-ойсторонамипроводника, (6.18) сопротивление R проводника и получаем закон Ома для однородного участка цепив следующем дифференциальномвиде:

I = φ₁ - φ₂/R ↔ I = Edl /R ↔ jdS = EdldS/ρ_сdl ↔ j = E/ρ_с ↔ j = σE, (6.19)

где переход от выражения в скалярной формы для модуля j вектора j плотности электрическоготока к выражению в векторной форме правомерен вследствие коллинеарности вектора j плотности электрическоготока в проводнике векторуE напряжённости электрического поля в этом проводнике и одинакового направления этих векторов; σ - удельная объёмная проводимость проводящего материала проводника.

Выражение (6.19) является законом Омав дифференциальномвиде, согласно которому вектор j плотности электрическоготока в рассматриваемой точке проводящейсреды коллинеарен вектору E напряжённости электрического поля в этой рассматриваемой точке проводящейсреды и оба этих вектора имеют одинаковое направление.

Выражение (6.6) j= q₊ n₊u₊ + |q_-|n_-u_- для модуля j вектора j плотности электрическоготока в металлах, где носителями электрическоготокаявляютсяэлектроны, вследствие коллинеарности вектора j плотности электрическоготока в проводнике среднему значению вектора <u_i > скорости движенияэлектронов и одинакового направления этих векторов имеет следующий вид: j = en_-<u_i >, (6.20)

где e, n_- - соответственно модуль заряда и концентрация электронов в материале проводника.

Подставляем (6.19) в (6.20) и получаем следующее выражение, связывающее среднее значение вектора <u_i > скорости движенияэлектронов в проводнике в рассматриваемой точке проводящейсреды с векторомE напряжённости электрического поля в этой рассматриваемой точке проводящейсреды проводника: <u_i > = σE/e n_-. (6.21)

Закон Ома для неоднородного участка цепи в дифференциальном виде

На (рис.6.6) неоднородном участке цепи на носители электрического тока кроме (6.14) вектораE напряжённости электрического поля действует вектор E^* напряжённости сторонних сил, который способен (6.1) вызвать упорядоченное движенияносителей электрического тока, вследствие чегозакон Ома для неоднородного участка цепи в дифференциальном виде по аналогии с (6.19) имеет следующий вид: j = σ(E + E^*), (6.22)

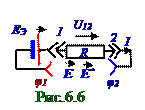
поперечного сечения проводника вектора j плотности электрическоготока согласно (6.22) имеет место следующее выражение: j_n = σ(E_n+E_n^*), (6.23) где E_n, E_n^* - проекции на n нормаль к элементарнойповерхности dS площадью поперечного сечения проводника векторов соответственно E, E^* напряжённостей электрического поля, сторонних сил могут быть положительными или отрицательными в зависимости от сонаправленности или противонаправленности вектору j плотности электрическоготока.

Сила I тока (рис. 06.0.5) в проводнике с учётом выражения (6.6) имеет следующий вид:

I = j_nS = jS ↔ j = I/S, (6.24)

где S - площадь поперечного сечения проводника; j_n - проекция на n нормаль к плоской

S площади поперечного сечения проводника вектора j плотности электрическоготока, равная модулю j этого вектора j плотности электрическоготока, поскольку вектор j плотности электрическоготока направлен по n нормали к плоской S площади поперечного сечения проводника. Подставляем (6.24) в (6.23) и получаем следующее выражение закона Ома для неоднородного участка цепи в дифференциальном виде: I/S = σ(E_n+E_n^*) ↔ I/S = (1/ρ_с)(E_n+E_n^*) ↔

↔ Iρ_с/S = (E_n+E_n^*), (6.25) где ρ_с - объёмное сопротивление проводящего материала проводника.

 

Закон Ома для неоднородного участка цепи в интегральном виде

 

Проведём интегрирование (6.25) по элементарной dl длине проводника от (рис. 06.0.6) его 1начала до 2 конца: 2 2 2 2 2 2

∫ (Iρ_с/S) dl = ∫E_n dl +∫E_n^*dl ↔ I∫(ρ_с/S) dl = ∫E_ndl +∫E_n^*dl ↔ IR =(φ₁ - φ₂) + ε_э ↔

1 1 1 1 1 1 ↔ U₁₂ = (φ₁ - φ₂) + ε_э, (6.26)

где U₁₂ = IR - напряжениемежду 1началом и 2 концом проводника, имеющего R сопротивление, по которому протекает сила I тока;

2

∫E_ndl = φ₁ - φ₂- разность потенциаловмежду 1началом и 2 концом проводника R сопротивлением;

1

2

∫E_n^*dl= ε_э - электродвижущая сила(ЭДС), действующая между 1началом и 2 концом проводника

1

R сопротивлением.

ЭДС записывают со знаком "+", если её направление совпадает при обходе электрической цепи с направлением U₁₂ напряжениямежду 1началом и 2 концом проводника R сопротивлением, как это изображено на рис. 6.6; если при обходе электрической цепи направление ЭДС противоположно направлению U₁₂ напряжениямежду 1началом и 2 концом проводника R сопротивлением, то ЭДС в выражении (6.26) записывают со знаком "-".

Участок электрической цепи называют неоднородным, если в этой электрической цепи, как на рис. 6.6, присутствует ЭДС.

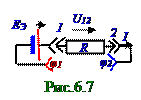
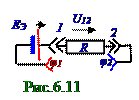
Участок электрической цепи называют однородным, если в электрической цепи ЭДС отсутствует. Тогда согласно (6.15) и рис.6.6 U₁₂ напряжениемежду 1-ой и 2-ойклеммамиравно разности φ₁ - φ₂ потенциалов в электрической цепи на нагрузке R сопротивлением. В неоднороднойэлектрической цепи постоянного электрического тока, т.е. при наличии (рис.6.7) в этой электрической цепи ЭДС ε_э величиной, в общейнагрузке R сопротивлениемпротекает следующий электрический ток I силой: I = U₁₂/R. (6.27) Подставляем (6.26) в (6.27) и получаем следующее выражение величины тока I силойвнеоднородной

электрической цепи постоянного электрического тока, т.е.закон Ома для неоднородного участка цепи постоянного электрического тока в интегральном виде: I = [(φ1 - φ2) + εэ]/R. (6.28) Если на внешних клеммах неоднорднойэлектрической цепи разность потенциалов φ1 - φ2 = 0, т.е. (рис.6.8) эта электрическая цепь постоянного

	электрического тока замкнута, то закон Ома для неоднородной цепи постоянного электрического тока в интегральном виде с учётом (6.28) принимает следующий вид: I = εэ /R, (6.29) где R - общеесопротивление всей электрической цепи постоянного электрического тока.

 

.

 

Разветвлённые цепи постоянного электрического тока: первое правило Кирхгофа

	Первоеправило Кирхгофа утверждает, что алгебраическая сумма n -токов, сходящихся в узле цепи постоянного электрического тока, равна нулю: n ∑Ii = 0.(6.30) i=1 Для A узла (рис. 06.0.9) в цепи постоянного электрического тока уравнение для токов

 

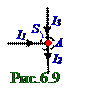
I₁, I₃ силы, входящих в A узел, и тока I силы, выходящего из A узла, согласно первомуправилу Кирхгофавыражение (6.26) принимает следующий вид: I₁ - I₂ + I₃ = 0 (6.31)

Первоеправило Кирхгофаявляется следствием (6.12) уравнения непрерывности постоянного электрического тока в интегральном виде, согласно которому общий электрическийток I₀ силой через воображаемую замкнутуюповерхность S площадью, ограничивающую A узел и пересекающий 3-ри проводника с токами I₁, I₂ и I₃ силы, равен нулю,т.е. I₀ = I₁- I₂ + I₃ = 0, вследствие отсутствия в этом A узле источниковили стоков носителей электрического тока.

 

Разветвлённые цепи постоянного электрического тока: второе правило Кирхгофа

 

Для замкнутой неоднородной цепи постоянного электрического тока, являющейся частью более общей цепи постоянного электрического тока, наличие которой на рис.6.10 представлено штриховымилиниями, выбрано направление обхода по часовой стрелке. Согласно (6.26) закону Ома для неоднородной цепи постоянного электрического тока для каждой ветви этой неоднородной цепи постоянного электрического тока имеют место следующие уравнения:

I1R1 = (φ1 - φ2) - ε1 - I2R2 = (φ2 - φ3) - ε2 ↔- ε1 - ε2 + ε3 = I1R1 - I2R2+I3R3. (6.32) I3R3 = (φ3 - φ1) +ε3 Суммирование (6.32) приводит к уравнению для замкнутой неоднородной цепи постоянного электрического тока, составленного по второмуправилу Кирхгофа следующим образом: а) при обходе (рис.6.10)замкнутой неоднородной цепи

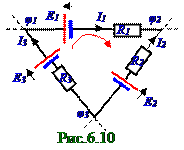
постоянного электрического тока по выбранному направлению в левой части этого уравнения записываются суммы ЭДС ε₁, ε₂,…, ε_n величиной со знаком "+", если направление обхода совпадает с направлением ЭДС, и со знаком "-", если направление обхода противоположнонаправлению ЭДС;

б) при обходе (рис.6.10)замкнутой неоднородной цепи постоянного электрического тока по выбранному направлению в правой части этого уравнения записываются суммы произведений токов I₁, I₂,…, I_n силы на величину R₁, R ₂,…, R _n сопротивлений, по которым протекают эти токи I₁, I₂,…, I_n силой, со знаком "+", если направление обхода совпадает с выбранным направлением токов I₁, I₂,…, I_n силы, и со знаком "-", если направление обхода противоположнонаправлению токов I₁, I₂,…, I_n силы.

Для общей цепи постоянного электрического тока, состоящейизнескольких замкнутых неоднородных цепей постоянного электрического тока, с использованием (6.30) первогои (6.32)второгоправил Кирхгофасоставляются независимыеуравнения, число которых достаточнодля определения неизвестных токов I₁, I₂,…, I_n силы, R₁, R ₂,…, R _n сопротивлений и ЭДС ε₁, ε₂,…, ε_n величиной.

Мощность и удельная мощность постоянного электрического тока

 

Работа A₁₂, совершаемая (рис. 06.0.6)электрическими силами, вследствие наличия разности

φ₁ - φ₂ потенциалов на внешних клеммах цепи постоянного электрического тока, и сторонними силами, вследствие наличия в этой цепи постоянного электрического тока источника ЭДС

ε_э величиной, по перемещению за промежуток Δt времени величины Δq заряда от 1-ой к 2-ой

	клемме имеет следующий вид: A12 = IпΔt(φ1 - φ2) + IпΔtεэ, (6.33) где (6.3) Iп = Δq/Δt - токпостояннойIпсилой в цепи постоянного электрического тока. Делим левую и правую части (6.29) на промежуток Δt времени и получаем следующее выражение A12/Δt работы, совершенную электрическими и

сторонними силамив цепи постоянного электрического тока за единицу t времени, т.е. в СИ за 1с, которое называют P мощностью постоянного электрического тока: P = A₁₂/Δt = I_п[(φ₁ - φ₂) + ε_э], (6.34)

Выражение (6.34) является выражением P мощности постоянного электрического тока в интегральномвиде, поскольку относится ко всей рассматриваемой цепи постоянного электрического тока. Эта P мощностьможетрасходоватьсяв рассматриваемой цепи постоянного электрического тока на совершение механической работы над внешними телами, например, на вращение ротора двигателя постоянноготока, на протекание химических реакций, например, на проведение реакции электролиза, на нагревание проводников этой рассматриваемой цепи постоянного электрического тока.

Удельная P_уд мощность - это мощностьв рассматриваемой цепи, развиваемая в единице V объёма проводника, т.е. в СИ в 1м³, через который протекает постоянный электрический ток. Выражениеудельной P_уд мощности в цепи постоянного электрического тока имеет следующий вид: P_уд = ΔP/ΔV,(6.35)

где ΔP - мощность, развиваемая в ΔV объёме проводникав рассматриваемой цепипостоянного электрического тока.

 

Закон Джоуля - Ленца в цепи постоянного электрического тока

 

Удельная P_уд (6.35) мощность в цепи постоянного электрического тока, в которой отсутствует совершение механической работы над внешними телами, а также отсутствуютхимическиереакции, т.е. постоянный электрический ток выполняет работу только по нагреванию проводника

R сопротивлением, с учётом выражения (6.23) связи постоянного тока I_п силы с U напряжением на этом проводнике R сопротивлением имеет следующий вид: P_уд = ΔP/ΔV = I_п[(φ₁ - φ₂) + ε_э]/ΔV = I_пU/ΔV = I_п²R/ΔV= I_п²ρ_сΔl/ΔSΔSΔl= ρ_сI_п²/ΔS²= ρ_сj_п², (6.36) где ΔV, ρ_с, Δl, ΔS, j_п - соответственно объём, удельное (6.19) ρ_с объёмное сопротивление проводящего материала, длина, поперечное сечение и плотность тока, которое в пределах проводника R сопротивлением принято постоянным.

В (6.36) выражении, являющемся законом Джоуля - Ленца в цепи постоянного электрического тока I_п силы, плотность j_п тока для однородного участка цепи постоянного электрического тока имеет следующий вид: j_п = I_п /ΔS = (φ₁ - φ₂)/RΔS, (6.37)

где φ₁ - φ₂ - разность потенциалов в (рис.6.6) электрической цепи между между 1началом и

2 концом проводника R сопротивлением и ΔS поперечным сечением этого проводника.

 

Переходный процесс при разрядке конденсатора в цепи постоянного электрического тока

 

Конденсатор C ёмкостью в начальный момент tн времени имел начальное Uн напряжение и разряжается через резистор R сопротивлением вследствие замыкания Кл ключа. Заряд q на конденсаторе C ёмкостью и при t > tн времени уменьшается, поэтому dq/dt < 0. Ток I силы в цепи разрядки конденсатора согласно (6.8) в принятом на схеме (рис.6.12) положительном направлении имеет следующий вид: I = - dq/dt. (6.38) Напряжение U наконденсаторе C ёмкостью с момента tн времени начала

 

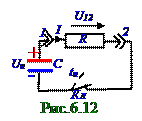
разрядки этого конденсатора имеет следующий вид: U = q/С,(6.39)

где q - заряд q на конденсаторе C ёмкостью в произвольный t момент времени при разрядке конденсатора, т.е. при t > t_н. Напряжение U₁₂ на резисторе R сопротивлением, по которому протекает (6.8) ток I силы имеет следующий вид: U₁₂ = IR = - Rdq/dt. (6.40)

Приравниваем (6.39) и (6.40), т.к. напряжение U наконденсаторе C ёмкостью согласно схеме (рис.6.12) равно напряжение U₁₂ на резисторе R сопротивлением и получаем следующее дифференциальное уравнение зависимости q заряда на конденсаторе от t времени разрядки этого конденсатора C ёмкостью через резистор R сопротивлением:

U = U₁₂ ↔ q/С = - Rdq/dt ↔ (dq/dt) + (q/RC) = 0. (6.41)Решение (6.41) дифференциального уравнения приводит к следующему выражению зависимости q зарядана конденсаторе от t времени разрядки этого конденсатора C ёмкостью через резистор

R сопротивлением: q = q_н exp(-t/τ), (6.42) где q_н - начальный зарядна конденсаторе C ёмкостью до t_н момента начала разрядки этого конденсатора через резистор R сопротивлением; τ = RC -постояннаявремени разрядки конденсатор C ёмкостью через резистор R сопротивлением.

Подставляем (6.42) в (6.38) и получаем следующее выражение зависимости тока I силы в цепи разрядки конденсатора от t времени разрядки этого конденсатора C ёмкостью через резистор R сопротивлением: I = - d(q_н exp(-t/τ)/dt = (q_н/RC) exp(-t/τ) = (U_н/R)exp(-t/τ) = I_нexp(-t/τ), (6.43) где q_н/C = U_н; I_н = U_н/R - соответственно напряжение и сила тока в цепи разрядки конденсаторав момент t_н времени начала разрядки конденсатора C ёмкостью через резистор R сопротивлением.

 

Переходный процесс при зарядке конденсатора в цепи постоянного электрического тока

 

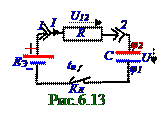
Конденсатор (рис.6.13) C ёмкостью до начального момента t_н времени не был заряжен и при t > t_н заряжается через резистор R сопротивлением вследствие замыкания Кл ключа. Заряд q на конденсаторе C ёмкостью и при t > t_н времени увеличивается, поэтому dq/dt > 0. Согласно рис.6.13 разность φ₂ - φ₁ потенциалов на обкладках конденсатора C ёмкостью равняется U напряжению на этих обкладках, т.е. φ₂ - φ₁= U, поэтомуразность φ₁ - φ₂ потенциалов внешних клеммах (рис.6.14) в неоднороднойэлектрической цепи постоянного электрического тока связаноc U напряжением на конденсаторе (рис.6.13) следующим выражением: φ₁ - φ₂ = - U. (6.44)

С учётом (6.28) и (6.44) выражение величины тока I силойв неоднороднойэлектрической цепи постоянного электрического тока (рис.6.14) имеет следующий вид: I = [(φ1 - φ2) + εэ]/R = (εэ - U)/R ↔ IR = εэ - U. (6.45) Ток I силы в цепи зарядки конденсатора согласно принятому на схеме (рис. 6.14) положительном направлении имеет следующий вид: I = dq/dt. (6.46) Напряжение U наконденсаторе C ёмкостью (6.39) связано (рис. 06.0.13) с q зарядом на конденсаторе C ёмкостью следующим выражением: U = q/С. (6.47) Подставляем (6.47) в (6.45), проводим дифференцирование левой и правой частей по t времени, получаем с учётом (6.46) I = dq/dt

 

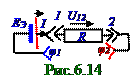
дифференциальное уравнение с разделяющимисяпеременными, в результате решения которого получается следующее выражение зависимости тока I силы в цепи зарядки конденсатора C ёмкостью в зависимости от t времени: I t

IR = ε_э - U ↔ IR = ε_э - (q/С) ↔ R(dI/dt)dt= -(1/C)(dq/dt)dt ↔ dI/I = -(1/RC)dt ↔ ∫dI/I = -(1/τ)∫dt ↔

I_нt_н=0

↔ lnI/I_н = - t/τ ↔ I = I_н e^-t/τ ↔ I = (ε_э /R)e^-t/τ, (6.48) где τ = RC - постояннаявремени зарядки конденсатора C ёмкостью через резистор R сопротивлением; I_н = ε_э/R - начальный ток I_н силы определяется подстановкой в выражение (6.45) начальногоU_н = 0 напряжения на конденсаторе в начальный момент t_н=0 времени.

Зависимость U напряжения на конденсаторе от t времени при подключении через резистор R сопротивлением с помощью Кл ключа источника с ЭДС, равной ε_э, получается следующей подстановкой (6.48) тока I силы в цепи зарядки конденсатора C ёмкостью в (6.45) выражение: IR = ε_э - U ↔ (ε_э /R)Re^-t/τ = ε_э - U ↔ U = ε_э (1 - e^-t/τ). (6.49)

Задача 1

	Конденсатор C ёмкостью (рис.6.15) в начальный момент t0 = 0 времени имел начальное Uн напряжение. Вывести выражение зависимости U напряжения на конденсаторе от t времени при подключении через резистор R сопротивлением с помощью Кл ключа источника с ЭДС, равной εэ. Сопротивление подводящих проводников и внутреннее сопротивление источника ЭДС считать равными нулю.

Согласно (6. 44) разность φ2 - φ1 потенциалов на внешних клеммах (рис. 6.16) в неоднороднойэлектрической цепи постоянного электрического тока связаноc U напряжением на конденсаторе (рис. 6.15), заменяющем эту разность φ2 - φ1 потенциалов, следующим выражением: φ1 - φ2 = - U. (6.50)

Дано: C, U_н, R, ε/ U(t) = ?

 

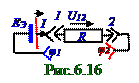
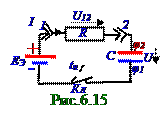
С учётом (6.45) и (6.50) выражение величины тока I силойв неоднороднойэлектрической цепи постоянного электрического тока (рис.6.16) имеет следующий вид:

I = (ε_э - U)/R ↔ IR = ε_э - U. (6.51)

Ток I силы в цепи зарядки конденсатора (6.46)согласно в принятом на схеме (рис.6.16) положительном направлении имеет следующий вид: I = dq/dt. (6.52)

Напряжение U наконденсаторе C ёмкостью (6.47) из раздела связано (рис.6.1) с q зарядом на конденсаторе C ёмкостью следующим выражением: U = q/С.(6.53)

Подставляем (6.53) в (6.51), проводим дифференцирование левой и правой частей по t времени,получаем с учётом (6.52) I = dq/dt дифференциальное уравнение с разделяющимисяпеременными, в результате решения которого получается следующее выражение зависимости тока I силы в цепи зарядки конденсатора C ёмкостью в зависимости от t времени: I t

IR = ε_э - U ↔ IR = ε_э - (q/С) ↔ R(dI/dt)dt= -(1/C)(dq/dt)dt ↔ dI/I = -(1/RC)dt ↔ ∫dI/I = -(1/τ)∫dt

I_нt_н=0

↔ lnI/I_н = - t/τ ↔ I = I_н e^-t/τ ↔ I = [(ε_э - U_н)/R] e^-t/τ, (6.54)

где τ = RC - постояннаявремени зарядки конденсатор C ёмкостью через резистор R сопротивлением; I_н = (ε_э - U_н)/R - начальный ток I_н силы определяется подстановкой в выражение (1.2) U_н напряжения на конденсаторе в начальный момент t_н=0 времени.

Зависимость U напряжения на конденсаторе от t времени при подключении через резистор R сопротивлением с помощью Кл ключа источника с ЭДС, равной ε_э, получается подстановкой (6.54) тока I силы в цепи зарядки конденсатора C ёмкостью в (1.2) выражение:

IR = ε_э - U ↔ [(ε_э - U_н)/R]Re^-t/τ = ε_э - U ↔ U = ε_э - (ε_э - U_н)e^-t/τ. (6.55)

Момент t₁ времениравенстванулюнапряжения на конденсаторе определится решением выражения (6.55) относительно t времени приравниваниемU₁ = 0 напряжения на конденсаторе: 0 = ε_э - (ε_э - U_н)e^{- t1/τ} ↔ t₁= RСln(ε_э - U_н)/ε_э. (6.56)

Согласно выражению (1.7) и качественному графику (рис. 6.17) зависимости U напряжения на конденсаторе от t времени при начальномUн напряжении (рис. 6.15) на конденсаторе, совпадающем по направлению с ЭДС, т.е. Uн>0, происходит дозарядконденсаторадо величины этой ЭДС, равной εэ.

Задача 2

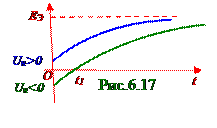
Лампочка представляет собой нелинейное R_л сопротивление с зависимостью тока I_л силойот U_л напряжения, изображённой на рисунке рис. 6.18, а зелёной линией. Найти P мощность, выделяемую на лампочке, если (рис.6.4, б) ЭДС источника постоянного тока имеет значение

E = 15 В, внутреннее r сопротивление имеет значение r = 3, 0 Ом, а подключенный параллельно лампочке резистор имеет значение сопротивления R = 2, 0 Ом.

Дано: R, ε, r, Iл = f(Uл)/P =? Согласно в принятом на схеме (рис.6.18, б) положительном направлении тока Iл силой через лампочку в (рис. 6.18, в) эквивалентной схеме Uл напряжение на этой лампочке имеет следующее значение: φ2 - φ1 = Uл ↔ φ1 - φ2 = - Uл .(6.57) С учётом (6.45) из раздела

и (6.57) выражение величины тока I_r силойв неоднороднойэлектрической цепи постоянного электрического тока (рис.6.18, в), включающей ЭДС, равной E = 15 В, и внутреннее r сопротивление этогоисточника постоянного тока, равное r = 3, 0 Ом, имеет следующий вид: I_r r = (φ₁ - φ₂) I_r + ε ↔ I_r = (ε/r) - (U_л/r). (6.58) С учётом (6.57) выражение величины тока I_R силойв однороднойэлектрической цепи постоянного электрического тока (рис. 6.18, в), включающей резистор сопротивлением R = 2, 0 Ом имеет следующий вид: I_R R = (φ₁ - φ₂) ↔ I_R = - U_л/R. (6.59) Суммируем левые и правые части (6.58) и (6.59), вследствие чегоимеет место следующее выражение: I_r + I_R = (ε/r) - U_л[(1/R) + (1/r)]. (6.60)

Для A узла (рис.6.18, в) в цепи постоянного электрического тока согласно (6.30) первомуправилу Кирхгофауравнение для токов I_r, I_R силы, входящих в A узел, и тока I_л силы через лампочку, выходящего из A узла, имеет следующий вид: I_r + I_R = I_л. (6.61)

Подставляем (6.61) в (6.60) и получаем следующее уравнение зависимости тока I_л силой через лампочку в зависимости от U_л напряжения на этой лампочке: I_л = (ε/r) - U_л[(1/R) + (1/r)]. (6.62)

Уравнение (6.62) в координатах (рис. 6.18, а) U_л напряжения, тока I_л силой графически представляет собой прямую линию, пересекающую ось абсцисс, т.е.когда I_л = 0, при следующем U_л0 напряжении на лампе:

0 = (ε/r) - U_л0 [(1/R) + (1/r)] ↔ U_л0 = (ε/r)/[(1/R) + (1/r)] = (15/3)/[(1/2) + (1/3)] = 6 В . (6.63)

Прямая линия, графически представляющая уравнение (6.63) в координатах (рис.6.18, а) U_л напряжения, тока I_л силой, пересекает ось ординат, т.е.когда U_л = 0, при следующем токе I_л0 силой через лампу: I_л0 = (ε/r) = 15/3 = 5 А. (6.64) Прямая линия, графически представляющая уравнение (6.63) в координатах U_л напряжения, тока I_л силой, изображёна на рис. 6.18, а синей линией и называется нагрузочнойхарактеристикой в данной задаче источника постоянного тока с ЭДС E = 15 В, внутренним r = 3, 0 Ом сопротивлением и подключенным параллельно лампочке резистором с R = 2, 0 Ом сопротивлением.

Пересечение этой нагрузочнойхарактеристики в C точке с графиком зависимости тока I_л силойот U_л напряжения на лампочке определяет режим работы лампы, т.е. через лампу протекает ток I_лC = 1 А силой при U_лC = 5 В напряжении на этой лампе. Поэтому P_C мощность, выделяемая на лампочке, имеет следующее значение: P = I_лC U_лC =1 А·5 В = 5 Вт.(6.65)

 

Задача 3

 

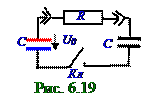
В схеме с резистором R сопротивлением и двумя конденсаторами одинаковой C емкости зарядили правый конденсатор до постоянного U₀ напряжения. В начальный t₀ = 0 момент времени

Кл ключ замкнули. Найти ток I(t) силой в цепи как функцию t времени и выделившуюся в резисторе

R сопротивлением Q теплоту за всё время разрядки конденсатора C емкости.

Дано: U₀, R, C/I(t) = ? Q = ?

До замыкания Кл ключа (рис. 6.19) величина q0 заряда на заряженном левом конденсаторе C ёмкостью определяется следующим выражением: U0 = q0/С.(6.66) После замыкания Кл ключа (рис.6.20) в произвольный t момент времени разрядки левого и зарядки правого конденсатора величины qл и qп зарядов соответственно на левом и правом конденсаторах C ёмкостью связаны с их Uп, Uл напряжениями следующими выражениями: Uп = (q0 - qл )/C; Uл = qл /C, (6.67) где qл - заряд, перешедший с левого на правый конденсатор. Согласно (6.32) второго правила Кирхгофа для а) контура имеет место с учётом (6.67) следующее выражение:

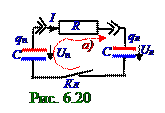
0 = IR - U_п + U_л ↔ I = (1/RC)[(q₀ - q_л ) - q_л] ↔

↔ dI/dt = - (2/RC)dq_л/dt ↔ dI/dt = - (2/RC)I ↔ dI/I = - (2/RC)dt,(6.68) где dq_л/dt = I - сила то

<== предыдущая лекция	|	следующая лекция ==>
Занятие 3. Электроёмкость, конденсаторы, энергия электростатического поля	|	Вектор индукции магнитного поля 1 страница

---

Дата добавления: 2016-02-14; просмотров: 789;

---