Емкость плоского конденсатора
Задача 3.1. Вычислить емкость плоского конденсатора, если площадь каждой его обкладки равна S, а расстояние между обкладками d. Между обкладками – вакуум. Размеры обкладок много больше расстояния между ними (d2 << S).
| S d | Решение.Сообщим обкладкам заряды +Q и –Q (рис. 3.2). Тогда поверхностная плотность заряда s = Q/S.
 Рис. 3.2 Рис. 3.2
|
| С = ? | |
Каждую обкладку в условиях данной задачи можно рассматривать как бесконечную заряженную плоскость. Напряженность поля бесконечной заряженной плоскости, как мы знаем, равна 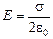 и не зависит от расстояния до плоскости. Напряженность поля каждой обкладки
и не зависит от расстояния до плоскости. Напряженность поля каждой обкладки 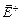 и
и 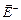 направлена, как показано на рис. 3.3.
направлена, как показано на рис. 3.3.
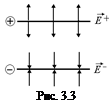 Согласно принципу суперпозиции
Согласно принципу суперпозиции 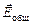 = =
= = 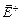 +
+ 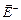 . Напряженность поля между обкладками равна
. Напряженность поля между обкладками равна
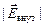 = |
= | 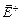 | + |
| + | 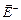 | =
| = 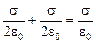 ,
,
а поле снаружи отсутствует, так как
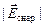 = |
= | 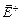 | – |
| – | 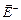 | =
| = 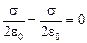 .
.
Договоримся, что потенциал отрицательно заряженных обкладок равен нулю: j = 0. Тогда разность потенциалов между обкладками равна потенциалу положительно заряженной пластины j+ и равна работе электрического поля в конденсаторе по перемещению единичного положительного заряда с верхней (положительной) обкладки на нижнюю (отрицательную):
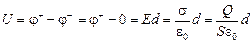 .
.
Тогда согласно формуле (3.1) емкость конденсатора составит
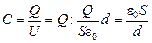 .
.
Ответ:
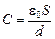 . (3.2)
. (3.2)
Заметим, что чем меньше расстояние между обкладками d, тем больше емкость конденсатора.
Задача 3.2. Как изменится результат задачи 3.1, если между пластинами конденсатора поместить диэлектрик с диэлектрической проницаемостью e?
| S, d, e | Решение.Диэлектрик ослабит поле между пластинами в e раз, поэтому напряженность поля в конденсаторе будет равна Е = s/ee0, тогда |
| С = ? | |
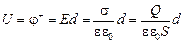 ,
,
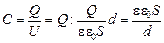 .
.
Ответ:
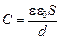 . (3.3)
. (3.3)
Таким образом, введение в пространство между обкладками конденсатора диэлектрика увеличивает емкость в e раз!
СТОП! Решите самостоятельно: А6–А8, В2.
Задача 3.3. Плоский конденсатор зарядили и отключили от источника напряжения. После этого увеличили расстояние между пластинами в 2 раза. Как изменились при этом емкость конденсатора, напряженность поля в конденсаторе, напряжение (разность потенциалов) между обкладками?
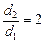
| Решение. 1.Согласно формуле (3.3) 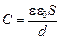 , поэтому , поэтому 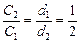 , т.е. емкость уменьшилась в 2 раза.
2. Поскольку конденсатор отключен от источника напряжения, то заряды на пластинах не могут измениться, , т.е. емкость уменьшилась в 2 раза.
2. Поскольку конденсатор отключен от источника напряжения, то заряды на пластинах не могут измениться,
|
| С2/С1 = ? Е2/Е1 = ? U2/U1 = ? | |
а значит, не меняется и поверхностная плотность зарядов s. Так как Е = s/e0, то напряженность не изменилась и Е2/Е1 = 1.
3. Поскольку U = Ed, то 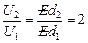 , т.е. напряжение возросло в 2 раза.
, т.е. напряжение возросло в 2 раза.
Ответ: С2/С1 = 1/2; Е2/Е1 = 1; U2/U1 = 2.
СТОП! Решите самостоятельно: А14, В9.
Задача 3.4. Плоский конденсатор подключен к источнику постоянного напряжения. Расстояние между его обкладками увеличили в 2 раза. Как изменились при этом емкость конденсатора, напряженность внутри конденсатора и напряжение между обкладками?
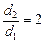
| Решение. 1.Емкость никак не зависит ни от напряжения, ни от заряда, поэтому она изменилась точно так же, как и в задаче 3.3: 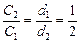 .
2. Поскольку конденсатор все время подключен к источнику напряжения, то напряжение на его обкладках все .
2. Поскольку конденсатор все время подключен к источнику напряжения, то напряжение на его обкладках все
|
| С2/С1 = ? Е2/Е1 = ? U2/U1 = ? | |
время постоянно, т.е. U2 = U1, или U2/U1 = 1.
3.Так как Е = 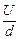 , то
, то 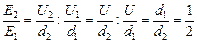 , т.е. напряженность поля уменьшилась в 2 раза. Это произошло потому, что заряд на обкладках уменьшился, т.е. часть заряда «вернулась» обратно в источник!
, т.е. напряженность поля уменьшилась в 2 раза. Это произошло потому, что заряд на обкладках уменьшился, т.е. часть заряда «вернулась» обратно в источник!
Ответ: С2/С1 = 1/2; U2/U1 = 1; Е2/Е1 = 1/2.
СТОП! Решите самостоятельно: А15, А16.
Задача 3.5. Плоский конденсатор зарядили и отключили от источника напряжения. После этого между обкладками вставили пластину из диэлектрика с диэлектрической проницаемостью e. Как изменились емкость, напряженность поля между обкладками и напряжение?
| e | Решение. 1.Согласно формуле (3.3) 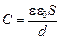 , поэтому емкость возрастет в e раз: С2/С1 = e.
2. Поскольку Е = s/ee0, а величина s не изменилась, то Е уменьшилась в e раз: Е2/Е1 = 1/e.
3. Так как U = Ed, то , поэтому емкость возрастет в e раз: С2/С1 = e.
2. Поскольку Е = s/ee0, а величина s не изменилась, то Е уменьшилась в e раз: Е2/Е1 = 1/e.
3. Так как U = Ed, то 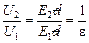 , т.е. напряжение также уменьшилось в e раз. , т.е. напряжение также уменьшилось в e раз.
|
| С2/С1 = ? Е2/Е1 = ? U2/U1 = ? | |
Ответ: С2/С1 = e; Е2/Е1 = U2/U1 = 1/e.
СТОП! Решите самостоятельно: А12, В4, С1.
Задача 3.4. Плоский конденсатор подключен к источнику постоянного напряжения. Как изменятся напряжение, напряженность поля между обкладками и заряд конденсатора, если между ними вставить пластинку из диэлектрика с диэлектрической проницаемостью e?
| e | Решение. 1. Из условия задачи ясно, что U = const, т.е. U2/U1 = 1. 2. Так как Е = U/d, то величина Е также не меняется: Е2/Е1 = 1. 3. Поскольку Е1 = s/e0, Е2 = s/ee0, и при этом Е1 = Е2, |
| Е2/Е1 = ? U2/U1 = ? q2/q1 = ? | |
то 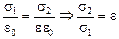 , т.е. поверхностная плотность заряда увеличилась в e раз. Так как q = sS, то
, т.е. поверхностная плотность заряда увеличилась в e раз. Так как q = sS, то 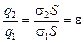 . Итак, величина заряда возросла в e раз, это увеличение «обеспечил» источник напряжения.
. Итак, величина заряда возросла в e раз, это увеличение «обеспечил» источник напряжения.
Ответ: q2/q1 = e; Е2/Е1 = U2/U1 = 1.
СТОП! Решите самостоятельно: В5, В7, В8.
Дата добавления: 2016-04-11; просмотров: 1987;
