Емкость уединенного проводника
Экспериментально установлено, что потенциал заряженного проводника прямо пропорционален его заряду:
j ~ q. (2.1)
Это позволяет ввести в рассмотрение величину, равную отношению заряда проводника к его потенциалу:
С = q/j. (2.2)
Величина С называется электрической емкостью проводника. В системе СИ [C] = [q]/[j] = Кл/В = Ф (фарад). Наряду с фарадом используются также микрофарад (1 мкФ = 10–6 Ф) и пикофарад (1пФ = 10–12 Ф).
Задача 2.1. Вычислить емкость шара радиуса R.
| R | Решение.Пусть заряд шара равен q, тогда его потенциал  , где , где  в СИ и k = 1 в СГСЭ. в СИ и k = 1 в СГСЭ.
|
| C = ? | |
Согласно формуле (2.2)
С = q/j = 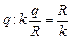 ,
,
тогда
в СИ: С = 4pe0R, (2.3)
в СГСЭ: C = R. (2.4)
Ответ: С = 4pe0R (СИ), C = R (СГСЭ).
Заметим, что из (2.4) следует, что электрическая емкость в системе СГСЭ измеряется в единицах длины: [C] = [R] = см.
СТОП! Решите самостоятельно: А1–А3, В2.
Читатель: А почему отношение q/j назвали именно электрической емкостью, а не как-нибудь еще?
Автор: Чем больше С, тем больший заряд можно поместить на данный проводник. В самом деле, если при данном q величина С велика, то величина j соответственно мала (согласно (2.2)). Значит, заряд на проводнике создает около себя относительно слабое электрическое поле, которое не сможет «пробить» воздух. Следовательно, заряд не будет стекать с нашего проводника.
Рассмотрим, как зависит емкость от диэлектрической проницаемости среды.
Задача 2.2.Вычислить емкость шара радиуса R, помещенного в среду с диэлектрической проницаемостью e.
| R e | Решение.Если мы поместим металлический шар в среду с диэлектрической проницаемостью e, то потенциал шара будет равен 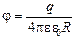 , а емкость , а емкость
|
| C = ? | |
С = q/j =  .
.
Ответ: С =  .
.
Итак, в среде емкость шара в e раз больше, чем емкость такого же шара в вакууме
С =  . (2.5)
. (2.5)
СТОП! Решите самостоятельно: А4, А5.
Читатель: Почему нельзя ввести понятия емкости диэлектрика?
Автор: Потому что потенциал разных точек диэлектрика различен и зависит от того, как именно распределен по поверхности заряд, так как заряды в диэлектрике не могут свободно перемещаться под действием электрического поля.
Читатель: А зависит ли электрическая емкость от материала проводника?
Автор: Нет. Формула (2.2) справедлива для любого проводящего материала. Но вот от присутствия поблизости других проводников, даже незаряженных, емкость проводника зависит очень сильно.
В самом деле, пусть рядом с заряженным шаром мы поместили незаряженный металлический стержень (рис. 2.1). Как Вы думаете, что произойдет?
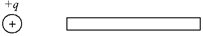 Рис. 2.1
Рис. 2.1
Читатель: Я думаю, что из-за индукции заряды на стержне перераспределятся (рис. 2.2).
 Рис. 2.2
Рис. 2.2
Автор: Совершенно верно. А как повлияют отрицательные заряды стержня на поле около нашего положительного заряженного шара: ослабят они его или усилят?
Читатель: Конечно, ослабят. Они же противоположного знака!
Автор: Значит, и потенциал шара уменьшится. А тогда как изменится емкость шара согласно формуле (2.2)?
Читатель: Возрастет! Получается, что, поднося к одному проводнику другой, мы увеличиваем его емкость?
Автор: Совершенно верно!
СТОП! Решите самостоятельно: В1, С1, С2.
Задача 2.3. Потенциал проводников с емкостями С1 = 6,0 пФ и С2 = 9,0 пФ равны соответственно j1 = 2,0×102 В и j2 = 8,0×102 В. Найти суммарный заряд и потенциал проводников после соединения их проводом. Индукцией пренебречь.
| С1 = 6,0 пФ = 6,0×10–12 Ф С2 = 9,0 пФ = 9,0×10–12 Ф j1 = 2,0×102 В j2 = 8,0×102 В | Решение. До соединения справедливо q1 = C1j1 и q2 = C2j2. Тогда общий заряд Q = q1 + q2 = C1j1 + C2j2, причем после соединения величина общего заряда измениться не могла. Подставим численные значения: |
| Q = ? j = ? | |
Q = C1j1 + C2j2 =
= 6,0×10–12 Ф × 2,0×102 В + 9,0×10–12 Ф × 8,0×102 В »
» 8,4×10–9 Кл.
Пусть после соединения заряды проводников стали равны 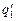 и
и 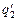 , тогда справедливы следующие соотношения:
, тогда справедливы следующие соотношения:

Из формулы (2) получаем 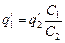 , подставим
, подставим 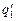 в формулу (1):
в формулу (1):
 ,
,
подставляя 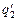 в формулу (3), находим
в формулу (3), находим
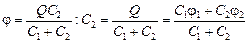 .
.
Подставим численные значения:
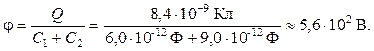
Ответ: Q = C1j1 + C2j2 » 8,4×10–9 Кл;
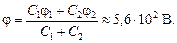
СТОП! Решите самостоятельно: А6, В4, С3.
Дата добавления: 2016-04-11; просмотров: 1334;
