Задачи средней трудности. В1. Два точечных заряда находятся в парафине на расстоянии 20 см

В1. Два точечных заряда находятся в парафине на расстоянии 20 см. На каком расстоянии они должны находиться в воздухе, чтобы сила взаимодействия между ними была такой же? Диэлектрическая проницаемость парафина e = 2,2.

В2. Сосуд с маслом, диэлектрическая проницаемость ко­торого e = = 5,0 помещен в вертикальное однородное электриче­ское поле. В масле находится во взвешенном состоянии алюминиевый шарик диаметром d = = 3,0 мм, имеющий заряд q = 1,0×10^–7 Кл. Определите напряженность электрического поля, если плотность алюминия r_Al = 2,6×10³ кг/м³ , а масла r_м = 0,90×10³ кг/м³.

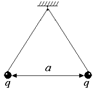Рис. 1.18

В3. Два одинаковых заряженных шарика, подвешенных на нитях равной длины в одной точке, разошлись в воз­духе на некоторый угол 2a. Какова должна быть плот­ность r материала шариков, чтобы при погружении их в керосин (диэлектрическая проницаемость e = 2,1) угол между нитями не изменился? Плотность керосина r_к = 0,80×10³ кг/м³.

В4. Заряженные шарики, подвешенные на длинных нитях так, как показано на рис. 1.18, помещены в транс­форматорное масло. Плотность материала шариков больше плотности масла r₀, начальное расстояние между шариками а. Определить расстояние b между шариками после опу­скания их в масло. Диэлектрическая проницаемость масла e.

В5. Два малых заряженных шара, расположенных на достаточно большом постоянном расстоянии друг от друга, помещаются последовательно в ряд сред с возрастающими диэлектрическими проницаемостями. При этом в одной серии опытов поддерживается все время постоянной величина зарядов шаров, в другой – остается постоянной разность потенциалов. Как в этих случаях будет меняться сила взаимодействия шаров с ростом диэлектрической проницаемости?

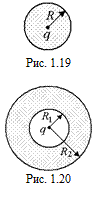
В6. Точечный заряд q находится в центре равномерно заряженного шара из диэлектрика радиусом R (рис. 1.19). Объемная плотность заряда r, диэлектрическая проницаемость e. Построить графики Е(r) и j(r). Нарисовать картину силовых линий.

В7. Точечный заряд q окружен незаряженным слоем диэлектрика с диэлектрической проницаемостью e (рис. 1.20). Построить графики Е(r) и j(r). Нарисовать картину силовых линий.

В8. Металлический шар радиусом R = 4,0 см заряжен до потенциала j₀ = 2,0 В. Определить напряженность и потенциал электростатического поля на расстояниях l₁ = 2,0 см и l₂ = 6,0 см от центра шара. Рассмотреть два случая: 1) шар находится в воздухе; 2) шар помещен в диэлектрик с диэлектрической проницаемостью e = 2,0.

В9. Две тонкие металлические концентрические сферы ра­диусами R₁ и R₂ (R₁ < R₂) погружены в диэлектрическую среду с проницаемостью e так, что диэлектрик проникает и в пространство между сферами. Внутренняя сфера обладает зарядом Q. Найти напряженность поля Е и потенциал j как функцию расстояния r от центра сфер.

В10. Напряженность электрического поля, создаваемого однородно заря­женной диэлектрической сферой радиуса r₀ (e = 2,0), изменяется при r < r₀ по закону Е = (1/3)(rr/e₀e) в диэлектрике. При радиусе, равном r₀ = 5,0 см, Е₁ = 2,0 В/м. Определить объемную плотность заряда r и зависимость Е от r при r > r₀.

В11. Две параллельные металлические пластины заря­жены так, что притягиваются с силой F. Изменится ли эта сила, если ввести между ними пластинку из диэлектрика?

В12. Два разноименно заряженных шарика находятся на некотором расстоянии друг от друга. Между ними вносят стеклянный стержень. Как изменится сила их взаимодействия?

В13. Можно ли при помощи электризации через влияние получить два куска диэлектрика, наэлектризованных разноименно, если диэлек­трик разрезать пополам?

Задачи трудные

С1. Найти натяжение нити, соединяющей одинаковые шарики радиуса r с одинаковыми зарядами Q. Один из ша­риков плавает на поверхности жидкости плотности r и диэлектрической проницаемости e, а второй шарик имеет массу т и висит на нити внутри жидкости. Расстояние между центрами шариков L.

С2. Два одинаковых алюминиевых шарика радиусом r на­деты на тонкий непроводящий стержень и опущены в керосин. Один из шариков закреплен, второй может свободно перемещаться вдоль стержня. У каждого миллиарда атомов неподвижного шарика от­нято по одному электрону и все эти электроны перенесены на подвиж­ный шарик. На каком расстоянии будут находиться в равновесии заряженные шарики при вертикальном положении стержня?

С3.Два маленьких одинаковых одноименно заряженных шарика радиуса r = 1 см подвешены на двух нитях длины l = 1 м. Заряды шариков q = =4×10^-6 Кл. Нити, на которых подвешены шарики, составляют угол a₁ = 90°.

1. Определить массу шариков.

2. Определить диэлектрическую проницаемость диэлектрика, если его плотность r = 0,8×10³ кг/м³ при условии, что при погружении шариков в жидкий однородный диэлектрик угол между нитями будет a₂ = 60°.

С4. Одинаковые шарики, подвешенные на закреплен­ных в одной точке нитях равной длины, зарядили одина­ковыми одноименными зарядами. Шарики оттолкнулись и угол между нитями стал равен a = 60°. После погруже­ния шариков в жидкий диэлектрик угол между нитями уменьшился до b = 50°. Найти диэлектрическую проницаемость среды. Выталкивающей силой пренебречь.

С5.Постройте графики зависимостей напряженности и потенциала электрического поля от расстояния для следующей системы: точечный заряд +Q находится в центре металлической сферической оболочки, к которой примыкает сферическая оболочка из диэлектрика (рис. 1.21).

С6.Радиус металлического шара R = 5,0 см а толщина сферического слоя эбонита, окружающего шар d = 5,0 см. Заряд шара q = 6,0×10^–9 Кл. Вычислить напряженность поля в точках, лежащих на расстояниях r₁ = 6,0 см и r₂ = 12 см от центра шара, и построить график зависимости напряженности от расстояния.

С7. Равномерно заряженный диэлектрический шар радиуса R₀ окружен металлическим сферическим слоем с внутренним радиусом R₁ и внешним радиусом R₂ (рис. 1.22). Заряд шара Q, диэлектрическая проницаемость e. Построить графики E(r) и j(r).

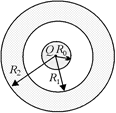
Рис. 1.22 Рис. 1.23 Рис. 1.24

С8. В пространстве, заполненном диэлектриком с диэлектрической проницаемостью e, находится сферическая полость радиуса R₀, внутри которой находится равномерно заряженный шар из такого же диэлектрика с зарядом Q и радиуса r₀ (рис. 1.23). Построить графики E(r) и j(r).

С9. Шар из диэлектрика радиуса R₀ равномерно заряжен электричеством с объемной плотностью заряда r и окружен сферическим слоем из диэлектрика с внутренним радиусом R₁ и внешним радиусом R₂ (рис. 1.24). Диэлектрическая проницаемость e. Построить графики E(r) и j(r).

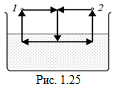С10. Как известно, сила взаимодействия между двумя электрическими зарядами меньше в воде, чем в воздухе. Казалось бы, этим можно воспользоваться для созда­ния «вечного двигателя» следующим образом: взяв два разноименных заряда в точках 1 и 2 (рис. 1.25), сблизить их в воздухе, затем одновременно опус­тить в воду, раздвинуть под водой, затем одновременно поднять в воздух в прежние положения, и далее повторять весь процесс сначала. При этом работа, полученная при сближении, больше той, которая затрачивается при раздвигании, так как силы электрического взаимодействия в воздухе больше, чем в воде. Где ошибка?

С11.Две заряженные параллельные плоскости с поверхностной плот­ностью заряда ±s, разнесены на расстояние d друг от друга и разделены прокладкой толщины h, диэлектрическая проницаемость которой e. Найти поверхностную плотность индуцированного поляризационного заряда на прокладке, напряженность электрического поля в пространстве между пластинами и разность потенциалов между ними.

С12.Две вертикально расположенные пластины заряжены так, что разность потенциалов между ними равна Dj = 400 В. Пластины погружают в масло. Какова поверхностная плотность связанных зарядов, если толщи­на масляного слоя d = 2,0 мм?

С13. Проводящий шар радиуса r с зарядом Q окружен слоем диэлектрика, внешний радиус которого R. Диэлектрическая проницаемость слоя e. Найдите поверхностную плотность заряда на внутренней и внешней поверхностях диэлектрического слоя. Нарисуйте линии напряженности электрического поля. Нарисуйте график зависимости напряженности и потенциала поля от расстояния до центра шара.

С14. Металлический шар радиуса R = 5,0 см, несущий заряд, равномерно распределенный с поверхностной плот­ностью s = 2,0×10^–9 Кл/м², погружают в керосин. Опре­делить величину и знак поляризационного заряда, наведенного на границе металл–диэлектрик.