КОМПЛЕКСНОЕ СОПРОТИВЛЕНИЕ. ЗАКОН ОМА ДЛЯ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
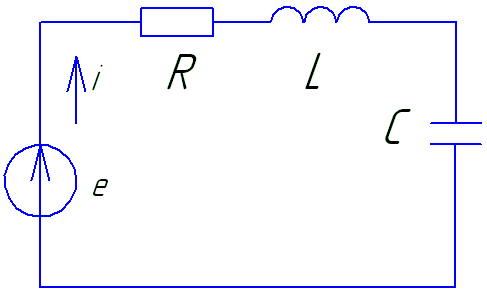
Рассмотрим схему (рис. 2-22), в которой резистор с сопротивлением R, катушка индуктивности с индуктивностью L и конденсатор ёмкостью С соединены последовательно. Схема питается от источника синусоидальной ЭДС.
| Рис. 2-22. Электрическая схема. |
Запишем для данной схемы уравнение по второму закону Кирхгофа для мгновенных значений:
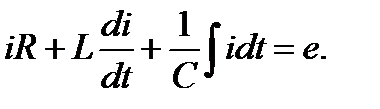 (2-52)
(2-52)
Пользуясь выше приведённой таблицей перехода от мгновенных значений к комплексным изображениям, получим:
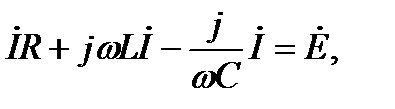 (2-53)
(2-53)
где 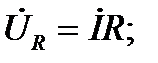

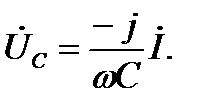
Направим вектор тока по вещественной оси комплексной плоскости и изобразим векторы напряжений на резисторе 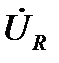 , на катушке индуктивности
, на катушке индуктивности 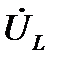 , на конденсаторе
, на конденсаторе 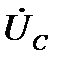 на комплексной плоскости (рис. 2-23):
на комплексной плоскости (рис. 2-23):
| Рис. 2-23. Векторная диаграмма цепи R,L,C. |

|

Получилась векторная диаграмма для рассматриваемой электрической схемы. Вектор напряжения на резисторе 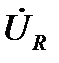 совпадает по фазе с вектором тока
совпадает по фазе с вектором тока 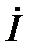 , так как отсутствуют множители j или –j. Вектор Напряжения на катушке индуктивности
, так как отсутствуют множители j или –j. Вектор Напряжения на катушке индуктивности 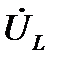 из-за наличия множителя j повёрнут относительно вектора тока
из-за наличия множителя j повёрнут относительно вектора тока 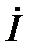 против часовой стрелки на 90°, то есть в направлении положительного отсчёта углов. Вектор напряжения на конденсаторе
против часовой стрелки на 90°, то есть в направлении положительного отсчёта углов. Вектор напряжения на конденсаторе 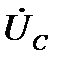 из-за наличия множителя –j повёрнут относительно вектора тока по часовой стрелке на 90°, то есть в направлении отрицательно отсчёта углов. На этой векторной диаграмме
из-за наличия множителя –j повёрнут относительно вектора тока по часовой стрелке на 90°, то есть в направлении отрицательно отсчёта углов. На этой векторной диаграмме 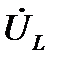 ›
› 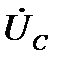 , поэтому в результате вектор тока
, поэтому в результате вектор тока 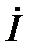 отстаёт на угол
отстаёт на угол 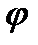 от вектора ЭДС
от вектора ЭДС 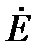 . В данном случае цепь имеет индуктивный характер.
. В данном случае цепь имеет индуктивный характер.
В выражении (2-53) вынесем ток за скобку:
 (2-54)
(2-54)
Множитель 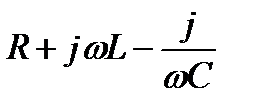 представляет собой комплекс, имеет размерность сопротивления и обозначается
представляет собой комплекс, имеет размерность сопротивления и обозначается 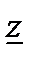 . Его называют комплексным сопротивлением:
. Его называют комплексным сопротивлением:
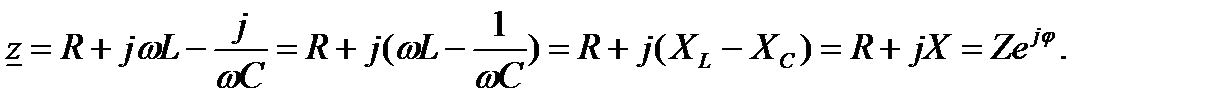 (2-55)
(2-55)
Здесь R -активное сопротивление цепи, 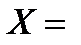
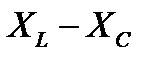 -реактивное сопротивление цепи, равное разности реактивного сопротивления катушки индуктивности
-реактивное сопротивление цепи, равное разности реактивного сопротивления катушки индуктивности 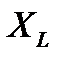 и реактивного сопротивления конденсатора
и реактивного сопротивления конденсатора 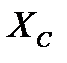 .
.
Уравнение (2-54) можно записать:
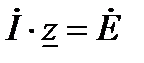 (2-56)
(2-56)
или
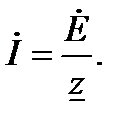 (2-57)
(2-57)
Уравнение (2-57) представляет собой закон Ома для цепи синусоидального тока.
| Рис. 2-24. Векторная диаграмма цепи R,L,C |

Дата добавления: 2016-03-15; просмотров: 2189;
