ТРЕУГОЛЬНИК ПРОВОДИМОСТЕЙ
Поделив все три стороны треугольника на  , получим треугольник проводимостей g, b, y (рис. 2-27).
, получим треугольник проводимостей g, b, y (рис. 2-27).
Изобразим отдельно треугольник проводимостей:
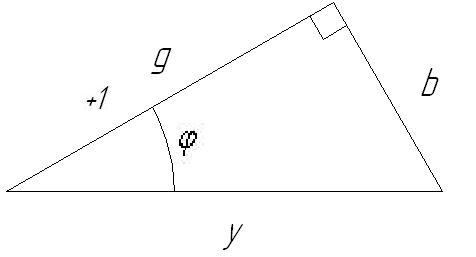
Рис. 2-27. Треугольник проводимостей.
Для рис. 2-27 можно записать:
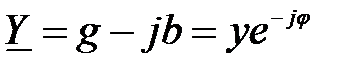 ; (2-66)
; (2-66)
 (2-67)
(2-67)
 (2-68)
(2-68)
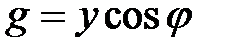 ; (2-69)
; (2-69)
 (2-70)
(2-70)
Объединим векторные диаграммы рис. 2-24 и рис. 2-26 (рис. 2-28);
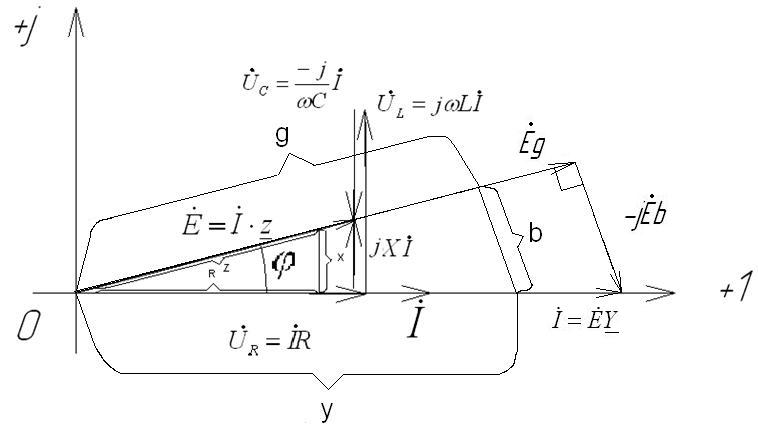
Рис. 2-28. Векторная диаграмма.
2-17. Операции с комплексными числами при расчёте цепей синусоидального тока
Любое комплексное число может быть записано в трёх формах: алгебраической, показательной и тригонометрической. Например:
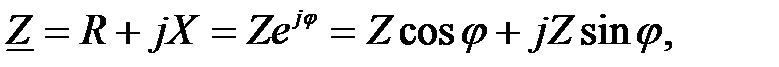 (2-71)
(2-71)
 -алгебраическая форма записи комплексного числа;
-алгебраическая форма записи комплексного числа;
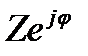 -показательная форма записи комплексного числа;
-показательная форма записи комплексного числа;
 -тригонометрическая форма записи комплексного числа.
-тригонометрическая форма записи комплексного числа.
На калькуляторе сложение, вычитание, умножение и деление комплексных чисел производится в алгебраической форме.
Ответ желательно иметь в двух формах: алгебраической и показательной. Комплексные сопротивления достаточно иметь в алгебраической форме для проведения расчётов. А вот комплексы токов ветвей, напряжений на отдельных участках схемы нужно обязательно перевести в показательную форму, так как переход от комплексных изображений к мгновенным значениям (синусоидам) производится от показательной формы.
Тригонометрическая форма записи является промежуточной и служит для перехода от показательной формы к алгебраической.
Покажем на примере расчёты с комплексными числами.
Прежде всего переключатель на калькуляторе DRG поставить в положение DEG, что означает измерение угла  в показательной форме в градусах.
в показательной форме в градусах.
Другие два положения переключателя: RAD-радианы, GRAD-грады.
Далее нужно определиться с точностью расчёта: сколько знаков после запятой мы хотим иметь. Так, если требуется делать расчёты, с точностью три знака после запятой, то мы нажимаем следующие клавиши:
| TAB |
2ndf 3
Чтобы вернуться в обычный режим, надо нажать следующие клавиши:
| TAB |
2ndf
Произведём расчеты следующего комплексного выражения:

Так как калькулятор считает комплексы только в алгебраической форме, то прежде всего комплексное число 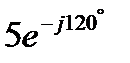 надо из показательной формы перевести в алгебраическую.
надо из показательной формы перевести в алгебраическую.
Включаем калькулятор, устанавливаем углы в градусах, точность расчёта, например, три знака после запятой и далее нажимаем клавиши:
| CPLX |
2ndf
Калькулятор перешёл в режим расчёта комплексных чисел. В правом верхнем углу возникает надпись CPLX.
Далее нажимаем:
2ndf a 5 a -120 b
2ndf a Калькулятор подготовлен к введению комплексного числа в показательной форме.
5 a -120 b вводится модуль комплекса 5 и угол -120º комплексного числа.
Далее нужно перевести введённое комплексное число в показательной форме в алгебраическую форму, чтобы калькулятор мог делать расчёты.
Для этого нажимаем дальше клавиши:
2ndf b Комплексное число  переведено в алгебраическую форму.
переведено в алгебраическую форму.
Далее нажимаем:
x -6 a 8 b
Умножили предыдущий комплекс на комплексное число -6+j8.
Далее нажимаем:
: 3 a -4 b
Разделили предыдущий результат на комплексное число 3-j4.
Далее нажимаем:
= И получаем ответ в алгебраической форме 5+j8,66.
Чтобы перевести ответ в показательную форму, нажимаем клавиши:
2ndf а Получаем ответ в показательной форме 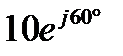 .
.
Никаких промежуточных записей не делаем. Только ответы в алгебраической и показательной форме.
На некоторых калькуляторах вместо клавиши 2ndf стоит клавиша shift того же назначения.
Дата добавления: 2016-03-15; просмотров: 2093;
