ПРЕОБРАЗОВАНИЕ ЗВЕЗДЫ В ТРЕУГОЛЬНИК И ТРЕУГОЛЬНИК В ЗВЕЗДУ

Условимся соединение трёх резисторов, имеющих вид трехлучевой звезды (рис. 1-31), называть соединение «звезда», а соединение трёх резисторов так, что они образуют собой стороны треугольника (рис. 1-32), называть соединением «треугольник».

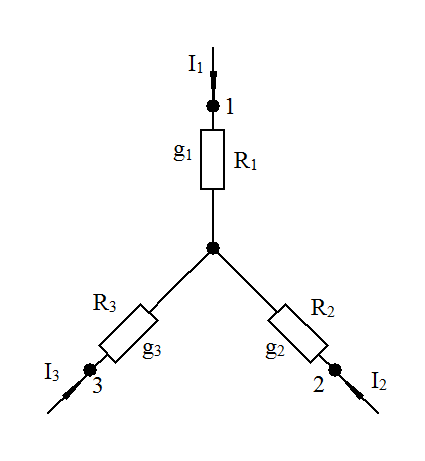
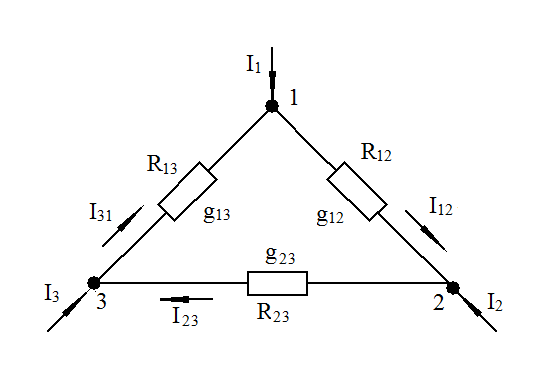
Рис. 1-31. Соединение «звезда» Рис. 1-32. Соединение «треугольник»

Обозначим потенциалы узлов 1, 2, 3 через φ₁, φ₂, φ₃. Токи, подтекающие к узлам 1, 2, 3 обозначим через I₁, I₂, I₃.

Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов φ₁, φ₂, φ₃ одноименных точек треугольника и звезды подтекающие к этим узлам токи будут одинаковые, то вся внешняя схема не заметит произведённой замены.

Выведем формулы преобразований. С этой целью выразим токи I₁, I₂ и I₃ в звезде и в треугольнике через разности потенциалов точек 1, 2, 3 и собственные проводимости.

Для звезды

I₁ + I₂ + I₃ = 0, (1-121)

I₁ = (φ₁ - φ₀)g₁; I₂ = (φ₂ - φ₀)g₂; I₃ = (φ₃ - φ₀)g₃. (1-122)

Подставим (1-122) в (1-121) и найдем ϕ₀

φ₁g₁ + φ₂g₂ + φ₃g₃ - φ₀(g₁ + g₂ + g₃) = 0.

Отсюда

φ₀ = 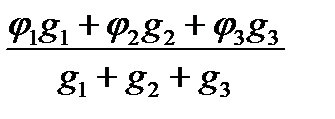. (1-123)

Далее, выведем φ₀ в выражении для тока I₁

I₁ = (φ₁ - φ₀)g₁ = 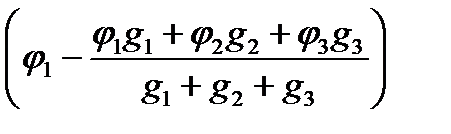; g₁ = 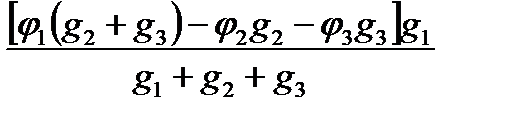.(1-124)

Обратимся к соединению треугольником. В соответствии с обозначениями на рис. 1-32:

I₁ = I₁₂ – I₃₁ = (φ₁ – φ₂)g₁₂ - (φ₃ – φ₁)g₁₃ = φ₁ (g₁₂ + g₁₃) – φ₃g₁₃ - ϕ₂g₁₂ . (1-125)

Так как ток I₁ в схеме рис.1- 31 должен равняться току I₁ в схеме рис. 1-32 при любых значениях потенциалов φ₁, φ₂, φ₃, то коэффициент при φ₂ в правой части (1-125) должен равняться коэффициенту при φ₂ в правой части (1-124), а коэффициент при φ₃ в правой части (1-125) должен равняться коэффициенту при φ₃ в правой части (1-124).

Следовательно,

g₁₂= ; (1-126)

g₁₃= 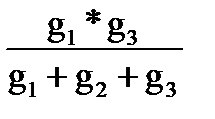. (1-127)

Аналогично,

g₂₃= 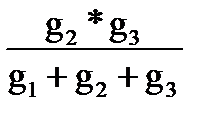. (1-128)

Формулы (1-126) – (1-128) дают возможность найти проводимости сторон треугольника через проводимости лучей звезды.

Из уравнений (1-126), (1-127), (1-128), выразим сопротивления лучей звезды

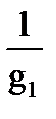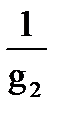R₁= ; R₂= ; R₃= .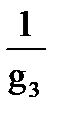

Через сопротивления сторон треугольника.

R₁₂= 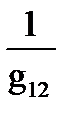; R₂₃= ; R₃₁= .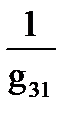

С этой целью запишем дробь, обратную (1-126)

R₁₂= 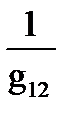= = 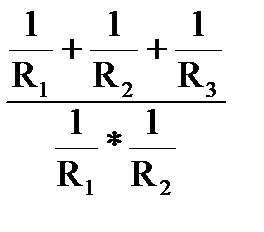= 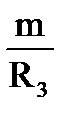. (1-129)

Здесь

m=(R₂*R₃ + R₁*R₃ + R₁*R₂). (1-130)

Аналогично

R₂₃= 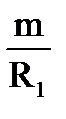; (1-131)

R₁₃= 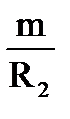. (1-132)

Отсюда

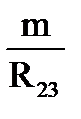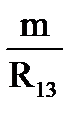R₁= ; R₂= ; R₃= 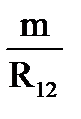. (1-133)

Подставим (1-133) в (1-130):

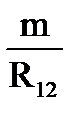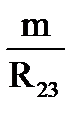
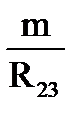
m = + + 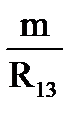= m² =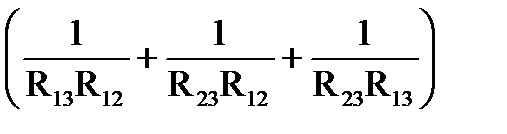

m² .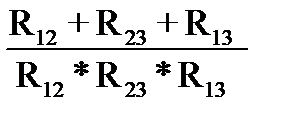

Следовательно

m = 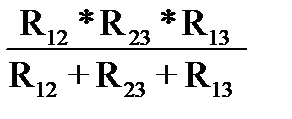. (1-134)

Подставим (133) в (132)

R₁= 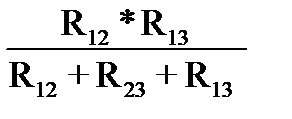; (1-135)

R₂= 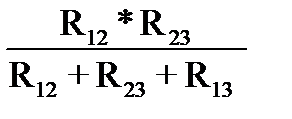; (1-136)

R₃= . (1-137)

Формулы (1-135) – (1-137) дают возможность найти сопротивления лучей звезды через сопротивления сторон треугольника.

Структура формул (1-135), (1-136), (1-137) легко запоминаются. В знаменателе стоит сумма сопротивлений треугольника. В числителе стоят произведения сопротивлений резисторов, примыкающих к узлам 1, 2, 3 соответственно.

Очень часто при расчёте электрических цепей оказывается полезным преобразовать треугольник в звезду или совершить преобразование звезды в треугольник. Практически чаще встречается потребность преобразования треугольника в звезду, чем в обратном преобразовании.

Полезность преобразования треугольника в звезду может быть проиллюстрирована, например, на схеме рис.1- 33.

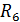
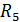
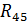
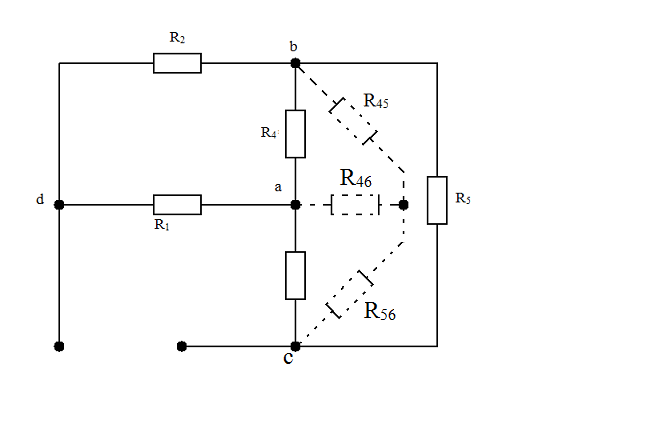
Рис. 1-33. Схема для определения входного сопротивления

Надо определить входное сопротивление схемы относительно зажимов «d» и «с». Соединение резисторов смешанное, нет явно выраженного последовательного или параллельного соединения.

Преобразуем треугольник резисторов R₄, R₅, R₆ в эквивалентную звезду. Штриховыми линиями на рис.1- 33 обозначена эквивалентная звезда.

Изобразим получившуюся схему на рис. 1-34.

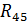
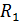
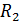
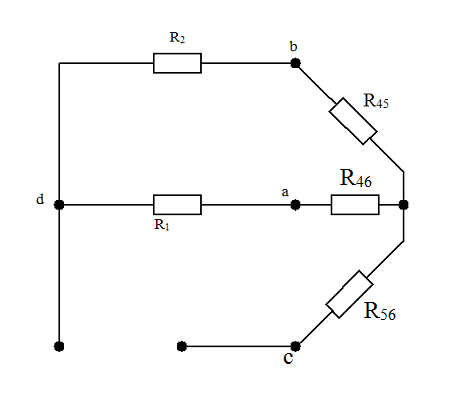
Рис. 1-34. Преобразованная схема

Согласно вышеизложенному

R₄₅= 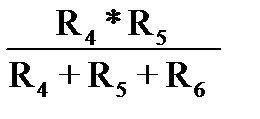; (1-138)

R₄₆= 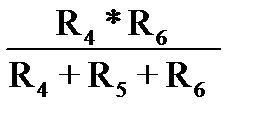; (1-139)

R₅₆= 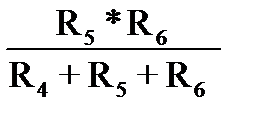. (1-140)

На схеме рис. 1-34 видно, что R₂ и R₄₅ соединены последовательно. R₁ и R₄₆ так же соединены последовательно. Эти упомянутые ветви соединены параллельно. И к этому сопротивлению последовательно включён R₅₆

R_вхdc = 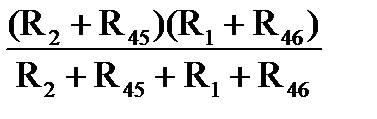+ R₅₆ . (1-141)

ТЕОРЕМА ВЗАИМНОСТИ

В любой, сколь угодно сложной линейной цепи ток в к-ой ветви, вызванный ЭДС Е_m, находящейся в m-ой ветви

I_k=E_mg_km (1-142)

будет равен току I_m в m-ой ветви, вызванному ЭДС Е_к (численно равной ЭДС Е_m), находящейся в к-ой ветви

I_m=E_kg_km. (1-143)

Согласно вышеизложенному взаимная проводимость между к-ой и m-ой ветвями g_km равно, взаимной проводимости между m-ой и к-ой ветвями g_mk, хотя определяются они по разным схемам:

g_km=g_mk. (1-144)

Поэтому и выполняется теорема взаимности.