Комплекс сандар өрісі
Егер рационал сандар өрісін қарастырғанда, өріс көпмүшеліктерінің түбірі бола бермейтінін көрдік. Мысалы 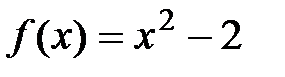 көпмүшелігінің рационал түбірі жоқ. Бұл өрісте
көпмүшелігінің рационал түбірі жоқ. Бұл өрісте 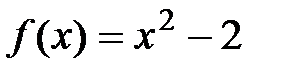 көпмүшелігі шығарылмайтын болады, себебі оның нақты түбірлері жоқ. Ең көп кездесетін сандық өріс – комплекс (кешен) сандар өрісі. Бұл өрісте кез-келген комплекс саннан
көпмүшелігі шығарылмайтын болады, себебі оның нақты түбірлері жоқ. Ең көп кездесетін сандық өріс – комплекс (кешен) сандар өрісі. Бұл өрісте кез-келген комплекс саннан  -дәрежелі түбір алынады.
-дәрежелі түбір алынады.
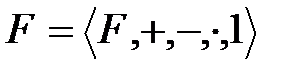 - өріс, ал
- өріс, ал 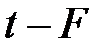 өрісіне тиісті емес элемент.
өрісіне тиісті емес элемент. 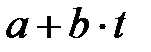 өрнегі болсын, мұндағы
өрнегі болсын, мұндағы  және
және 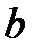
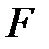 өрісінің кез-келген шамалары, оны
өрісінің кез-келген шамалары, оны  бойынша
бойынша 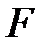 өрісінің сызықтық көпмүшелігі деп атайды.
өрісінің сызықтық көпмүшелігі деп атайды. 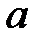 және
және 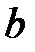 шамалары
шамалары 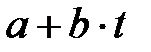 көпмүшелігінің коэффициенттері.
көпмүшелігінің коэффициенттері.
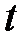 бойынша екі сызықтық көпмүшелік тең болады, егер олардың қосылғыштары бірдей болса.
бойынша екі сызықтық көпмүшелік тең болады, егер олардың қосылғыштары бірдей болса. 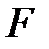 өрісінің кез-келген
өрісінің кез-келген 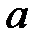 және
және 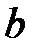 шамалары үшін:
шамалары үшін:
1) 
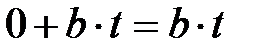
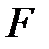 өрісінің
өрісінің 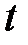 бойынша барлық сызықтық көпмүшелігінің жиынын
бойынша барлық сызықтық көпмүшелігінің жиынын  деп белгілейік:
деп белгілейік:
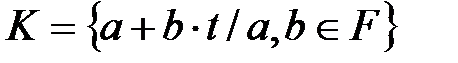
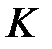 жиынында
жиынында 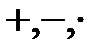 амалдарын келесі формулалармен анықтайық:
амалдарын келесі формулалармен анықтайық:
2) 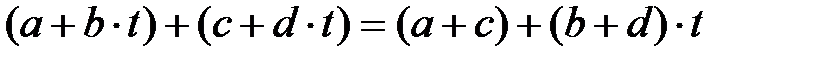
3) 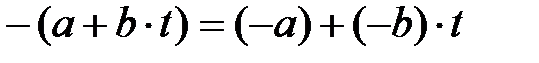
4) 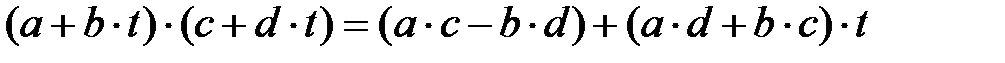
Кешен сандар өрісінде қосу және көбейту амалдары табиғи түрде жүргізіледі, тек қана 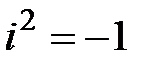 шарты бойынша.
шарты бойынша.
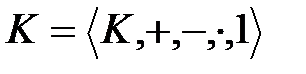 алгебрасын, сызықтық көпмүшеліктің алгебрасы деп атайды, мұндағы
алгебрасын, сызықтық көпмүшеліктің алгебрасы деп атайды, мұндағы 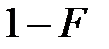 өрісінің бірлігі.
өрісінің бірлігі.
Теорема 3.1: 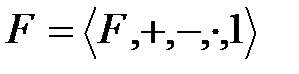 - өріс болсын.
- өріс болсын. 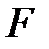 өрісіндегі
өрісіндегі 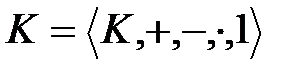 сызықтық көпмүшелігінің алгебрасы коммутативтік сақина, ал
сызықтық көпмүшелігінің алгебрасы коммутативтік сақина, ал 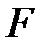 өрісі оның ішсақинасы.
өрісі оның ішсақинасы.
Дәлелдеу: 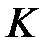 алгебрасының басты амалдары,
алгебрасының басты амалдары, 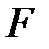 өрісінің сәйкес басты амалдарының жалғасы. Шынында да
өрісінің сәйкес басты амалдарының жалғасы. Шынында да 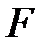 -гі кез-келген
-гі кез-келген 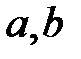 үшін
үшін 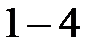 формуладан:
формуладан:
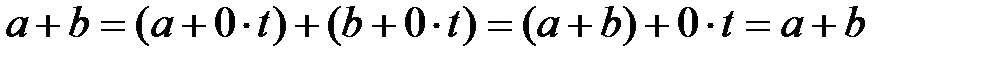
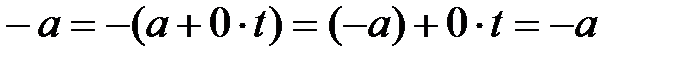
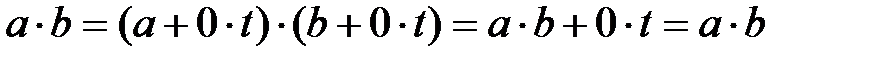
сонымен қатар 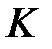 алгебрасындағы
алгебрасындағы 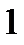 элементі
элементі 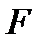 өрісінің бірлігі, яғни
өрісінің бірлігі, яғни 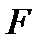 өрісі
өрісі 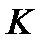 алгебрасының ішалгебрасы:
алгебрасының ішалгебрасы: 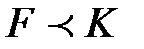

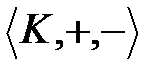 алгебрасы Абель тобы болып табылады.
алгебрасы Абель тобы болып табылады. 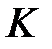 алгебрасында (2)
алгебрасында (2)
формула бойынша қосу коммутативті және ассоциативті, сол сияқты 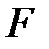 өрісінде де қосу коммутативті және ассоциативті.
өрісінде де қосу коммутативті және ассоциативті. 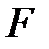 өрісінің нөлі
өрісінің нөлі 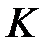 алгебрасына қатысты бейтарап шама, себебі
алгебрасына қатысты бейтарап шама, себебі 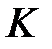 -ғы (1) және (2) формуладан
-ғы (1) және (2) формуладан 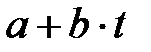 шамасы үшін:
шамасы үшін:
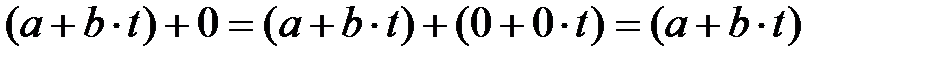
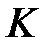 -ғы кез-келген
-ғы кез-келген 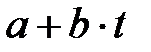 элементінің қарама-қарсы элементі бар,
элементінің қарама-қарсы элементі бар, 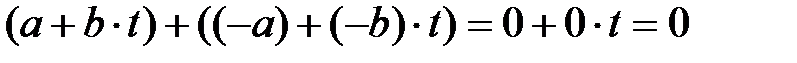
Осыдан 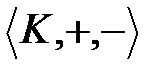 алгебрасы абель тобы болып табылады.
алгебрасы абель тобы болып табылады.
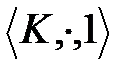 алгебрасы коммутативті моноид. Шынында да (4) формула бойынша
алгебрасы коммутативті моноид. Шынында да (4) формула бойынша 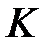 алгебрасындағы көбейту коммутативті, сол сияқты
алгебрасындағы көбейту коммутативті, сол сияқты 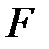 өрісінде де көбейту коммутативті.
өрісінде де көбейту коммутативті. 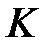 алгебрасының ассоциативті көбейтусін тексерейік:
алгебрасының ассоциативті көбейтусін тексерейік:
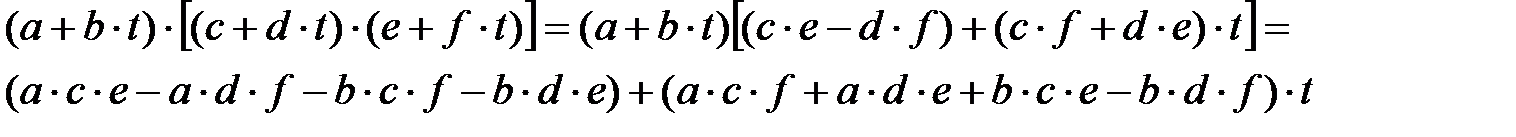
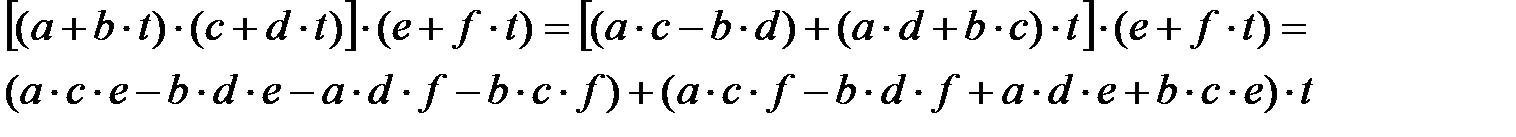
осыдан:
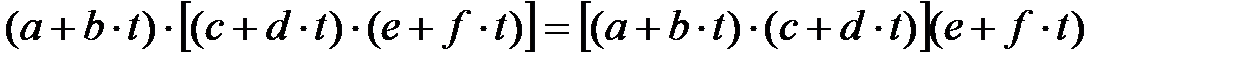
 алгебрасының көбейтіндісіне қатысты
алгебрасының көбейтіндісіне қатысты  өрісінің бірлігі бейтарап шама, себебі:
өрісінің бірлігі бейтарап шама, себебі: 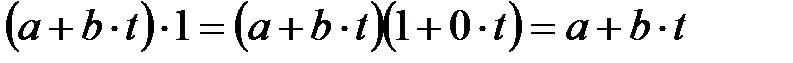
Осыдан 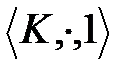 алгебрасы коммутативті моноид екені анықталды.
алгебрасы коммутативті моноид екені анықталды.
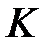 алгебрасында көбейту қосуға қатысты дистрибутивті:
алгебрасында көбейту қосуға қатысты дистрибутивті:
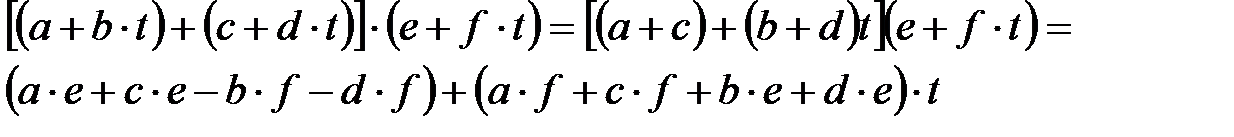
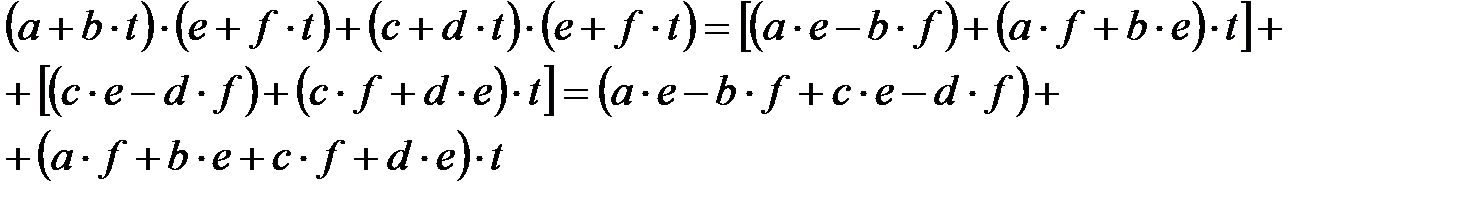
осыдан:

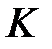 коммутативті сақина екені дәлелденді, яғни
коммутативті сақина екені дәлелденді, яғни 
 өрісі
өрісі 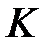 сақинасының ішсақинасы болады.
сақинасының ішсақинасы болады.
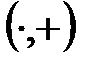 коммутативті және ассоциативті амалдары және дистрибутивті қатыс арқылы байланысты, ал оларға кері амалдар: - және
коммутативті және ассоциативті амалдары және дистрибутивті қатыс арқылы байланысты, ал оларға кері амалдар: - және 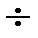 (0-ге бөлуден басқа) бар.
(0-ге бөлуден басқа) бар.
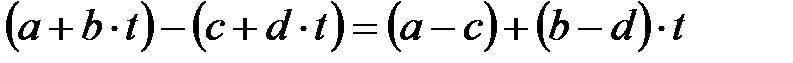 ,
, 
Олай болса кешен сандар - өріс құрайды,  ¢ деп белгіленеді. Бұл өріс
¢ деп белгіленеді. Бұл өріс 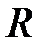 нақты сандар өрісінің алгебралық кеңейтілуі және
нақты сандар өрісінің алгебралық кеңейтілуі және 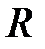 өрісіне
өрісіне 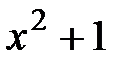 жиынына
жиынына 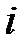 түбірінің қосылуы арқылы шығарылады. ¢ өрісі алгебралық тұйық: ¢- гі кез-келген коэфициентімен көпмүшелік, осы өрісте сызықтық көбейткіштерге жіктеледі. Кешен сандар өрісі
түбірінің қосылуы арқылы шығарылады. ¢ өрісі алгебралық тұйық: ¢- гі кез-келген коэфициентімен көпмүшелік, осы өрісте сызықтық көбейткіштерге жіктеледі. Кешен сандар өрісі  өрісінің жалғыз минималь кеңейтілуі, мұнда
өрісінің жалғыз минималь кеңейтілуі, мұнда 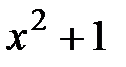 теңдеуінің түбірі болады.
теңдеуінің түбірі болады.
Анықтама: Комплекс (кешен) сандар өрісі деп нақты сандар өрісінің комплексті кеңейтілуін айтады.
Егер 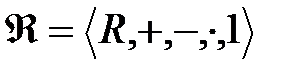 - нақты сандар өрісі, ал ¢–кешен сандар өрісі,
- нақты сандар өрісі, ал ¢–кешен сандар өрісі, 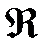 өрісінің комплексті кеңейтілуі. ¢ өрісінің негізгі жиынын
өрісінің комплексті кеңейтілуі. ¢ өрісінің негізгі жиынын  деп белгілейміз.
деп белгілейміз.  жиынының шамаларын кешен сандар деп атаймыз.
жиынының шамаларын кешен сандар деп атаймыз. 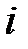 кешен саны,
кешен саны, 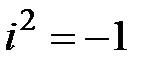 және
және  -нан кез-келген
-нан кез-келген 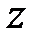 кешен саны
кешен саны 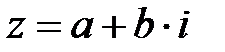 өрнегімен берілген, мұндағы
өрнегімен берілген, мұндағы  , ол
, ол 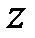 санының алгебралық формасы деп аталады.
санының алгебралық формасы деп аталады.
Теорема 3.2:  ¢=
¢= 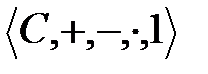 - кешен сандар өрісі
- кешен сандар өрісі 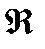 нақты сандар комплексті кеңейтілуі және
нақты сандар комплексті кеңейтілуі және 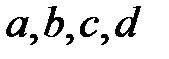 нақты сандар. Онда:
нақты сандар. Онда: 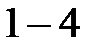 формулалар және
формулалар және
1. Егер  , онда
, онда 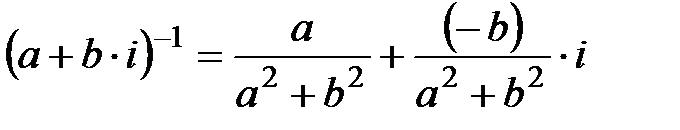
Дәлелдеу:  , егер
, егер 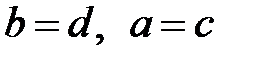 . Ал егер
. Ал егер 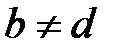 , онда
, онда 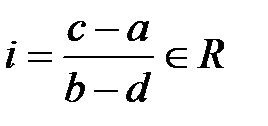 және
және 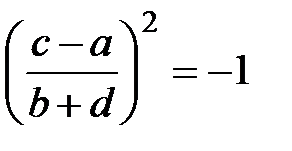 , бірақ бұл мүмкін емес, яғни
, бірақ бұл мүмкін емес, яғни 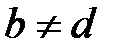 болу мүмкін емес. Егер
болу мүмкін емес. Егер 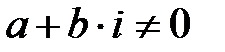 , яғни
, яғни  немесе
немесе 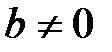 өрістің нөлдік емес екі шамасының өрнегі нөлге тең емес,
өрістің нөлдік емес екі шамасының өрнегі нөлге тең емес,
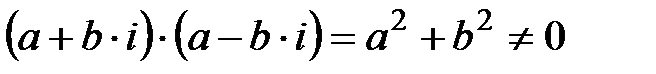
Анықтама: Егер 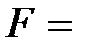
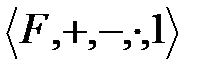 - өріс, мұндағы әрбір шаманың квадраты
- өріс, мұндағы әрбір шаманың квадраты 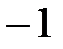 –ден өзгеше.
–ден өзгеше. 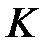 өрісі
өрісі 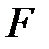 -өрісінің комплексті кеңейтілуі деп аталады, егер келесі шарттар орындалса:
-өрісінің комплексті кеңейтілуі деп аталады, егер келесі шарттар орындалса:
(1) Егер 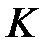 өрісінің ішөрісі
өрісінің ішөрісі  болса
болса
(2) 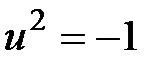 болатындай,
болатындай, 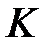 -де
-де 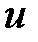 шамасының болуы.
шамасының болуы.
(3) 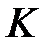 -өрісінде
-өрісінде 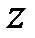 шамасының
шамасының  түрінде берілуі, мұндағы
түрінде берілуі, мұндағы 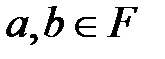 .
.
Сөйлем: 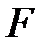 – кез-келген шамасының квадрты
– кез-келген шамасының квадрты 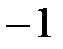 -ден өзгеше болатын өріс болсын.
-ден өзгеше болатын өріс болсын. 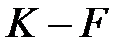 -өрісінің комплексті кеңейтілуі және
-өрісінің комплексті кеңейтілуі және 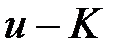 өрісінің шамасы, (2) және (3) шарттарды қанағаттандыратын. Онда
өрісінің шамасы, (2) және (3) шарттарды қанағаттандыратын. Онда 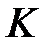 өрісінің
өрісінің 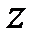 шамасы
шамасы  түрінде берілсе, мұндағы
түрінде берілсе, мұндағы 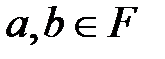
Дәлелдеу: 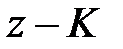 өрісінің кез-келген шамасы. (4)
өрісінің кез-келген шамасы. (4) 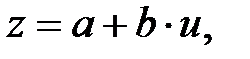
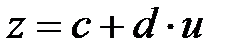 өрнегімен берілсін, мұндағы
өрнегімен берілсін, мұндағы  . Егер
. Егер 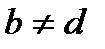 , онда
, онда 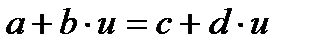 және
және 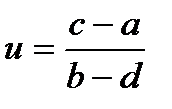

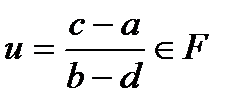 және
және 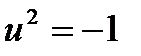 , бірақ та бұл
, бірақ та бұл 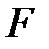 -өрісінің кез-келген шамасының квадраты
-өрісінің кез-келген шамасының квадраты 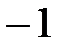 -ге тең деген шартқа қарсы. Сондықтан
-ге тең деген шартқа қарсы. Сондықтан  мүмкін емес,
мүмкін емес, 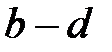 және (4) формуладан
және (4) формуладан 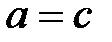 .
.
Анықтама: 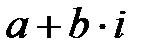
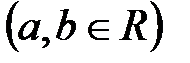 кешен санының модулі деп
кешен санының модулі деп  санынан арифметикалық квадрат түбір, яғни
санынан арифметикалық квадрат түбір, яғни 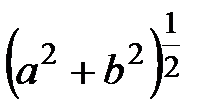 саны.
саны.  кешен санының модулі
кешен санының модулі  немесе
немесе 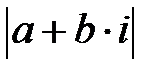 деп белгіленеді. Сондықтан, анықтама бойынша,
деп белгіленеді. Сондықтан, анықтама бойынша, 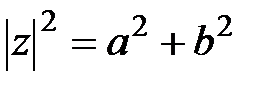
Теорема 3.3: 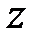 және
және 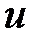 кез-келген кешен санына:
кез-келген кешен санына:
(1) 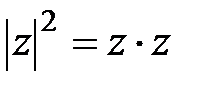
(2) 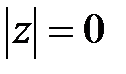 сонда ғана, егер
сонда ғана, егер 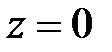
(3) 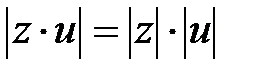
(4) 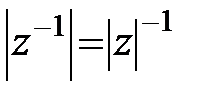 егер
егер 
(5) 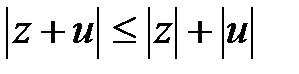
(6) 
(7) 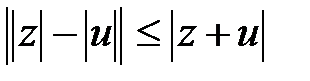
Дәлелдеу: 1 Егер 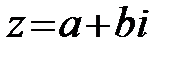 , онда
, онда  және
және 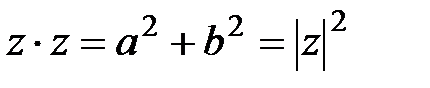
2. Егер  , онда
, онда 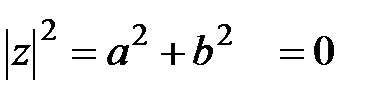 , себебі
, себебі  және
және 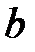 нақты сандар, онда
нақты сандар, онда 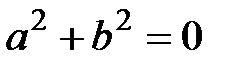 болғаннан
болғаннан  , яғни
, яғни 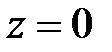 .
.
3. (1)-қатысты 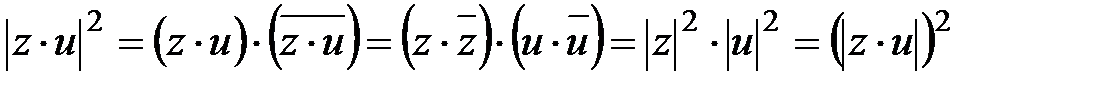
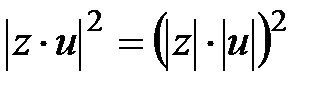 теңдігінен (3) формула шығады.
теңдігінен (3) формула шығады.
4. (3) қатысты 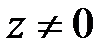
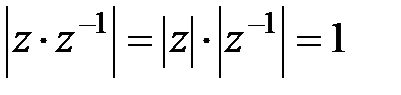
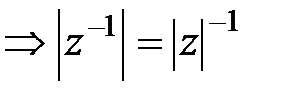
5. (1) қатысты 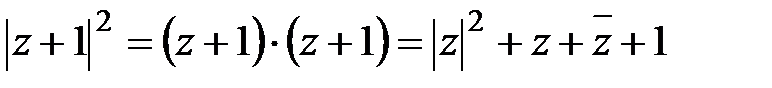
Осыдан басқа, егер 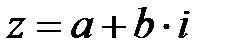 , онда
, онда 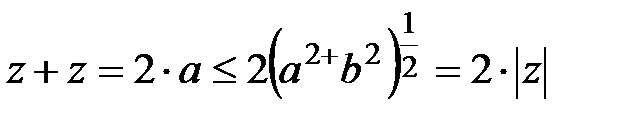 .
.
Сондықтан 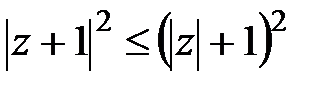 , осыдан
, осыдан 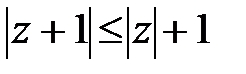
(3) формуланың негізінде және соңғы теңсіздіктен 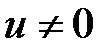 болғанда:
болғанда: 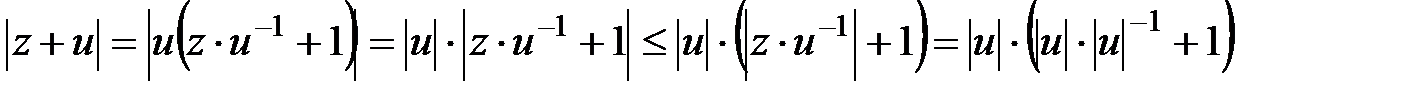 осыдан
осыдан 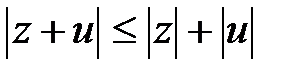
6. 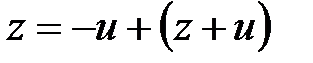 және
және 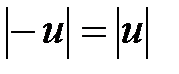 , онда (5) қатысты
, онда (5) қатысты  , осыдан
, осыдан 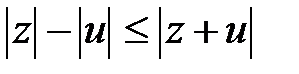
7. 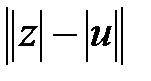 саны
саны  тең немесе
тең немесе  , онда (7) теңсіздік (6) теңсіздіктен шығады.
, онда (7) теңсіздік (6) теңсіздіктен шығады.
Сонымен, кешен сандар өрісінде кез-келген квадрат теңдеу шығарылады.
Мысалы:  теңдеуінің нақты түбірлері жоқ, себебі
теңдеуінің нақты түбірлері жоқ, себебі 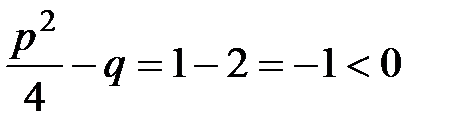 , бірақ оның кешен түбірлері бар:
, бірақ оның кешен түбірлері бар:
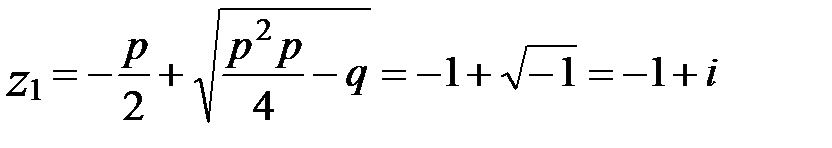


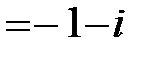
2. 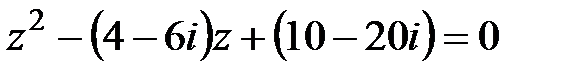 квадрат теңдеуін шешейік. Мұндағы
квадрат теңдеуін шешейік. Мұндағы  ; сондықтан
; сондықтан 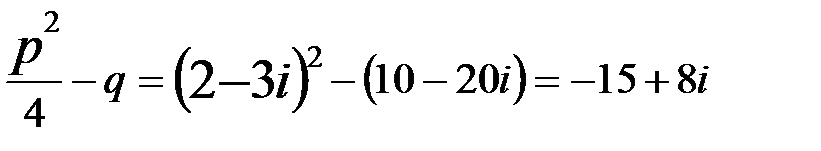
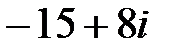 кешен санынан квадрат түбір аламыз, келесі формулалар бойынша
кешен санынан квадрат түбір аламыз, келесі формулалар бойынша

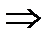
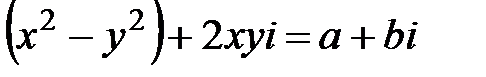
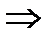
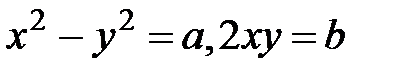
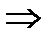


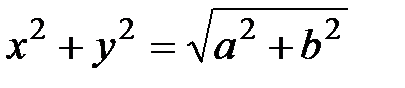 ,
, 
 ,
, 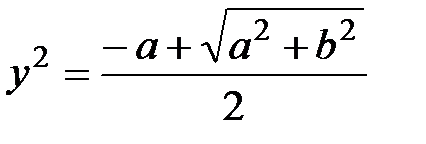

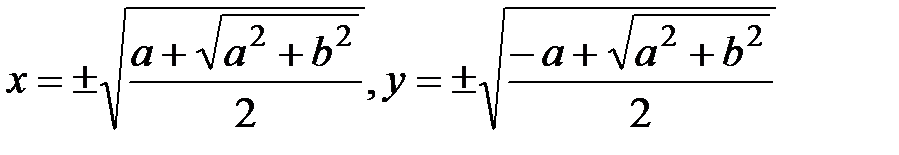 .
.
Соңғы формуладан 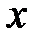 үшін «+» таңбаны алып шығарамыз:
үшін «+» таңбаны алып шығарамыз:
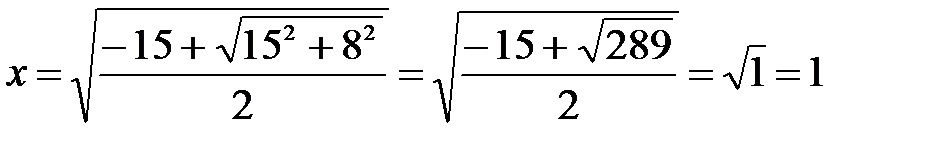
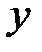 үшін де осы белгіні аламыз, себебі
үшін де осы белгіні аламыз, себебі 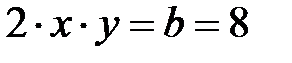 оң сан, сондықтан:
оң сан, сондықтан:
 , осыдан
, осыдан 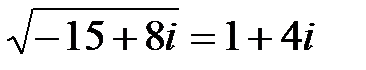 және
және  ,
, 
Дата добавления: 2016-04-02; просмотров: 5988;
