Рістің қарапайым қасиеттері
Өріс, ол – сақина. Сондықтан сақинаның барлық қасиеттері өрісте орындалады. Олардан басқа кез келген сақинада орындалмайтын мына қасиеттер орындалады:
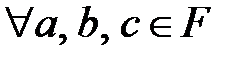 элементтері үшін
элементтері үшін
10. 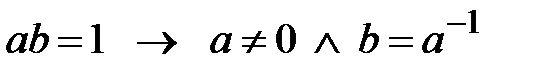 ; 20.
; 20. 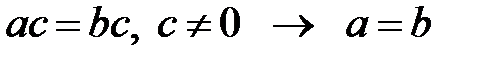 ;
;
30. 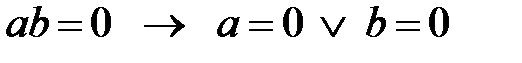 ; 40.
; 40. 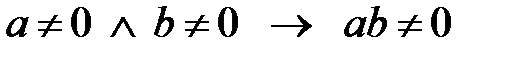 ;
;
50. 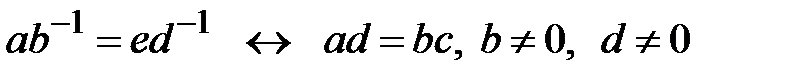
 (пропорция);
(пропорция);
60. 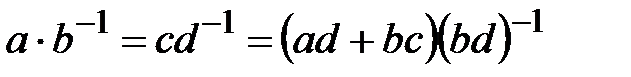 (ортақ бөлім);
(ортақ бөлім);
70. 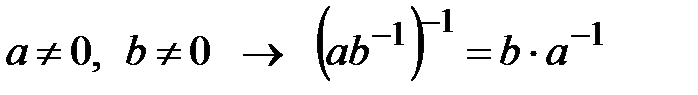 ;
;
80. 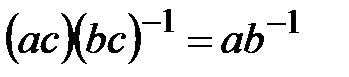 (қысқарту).
(қысқарту).
Дәлелдеуі:
10. 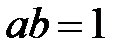 болса, онда
болса, онда 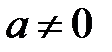 болады. Себебі
болады. Себебі 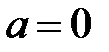 болса,
болса, 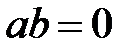 болмақ. Топтың 50 қасиеті бойынша
болмақ. Топтың 50 қасиеті бойынша 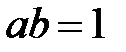 ден
ден 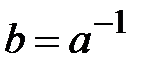 болды.
болды.
20. Топтың 70 қасиетінен шығады.
30. 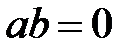 және
және 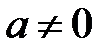 болсын. Онда
болсын. Онда 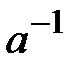 бар болады.
бар болады. 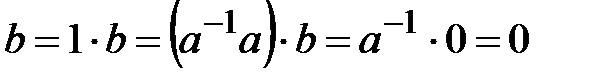 .
.
40. 30-ге контрапозицияны қолдансақ
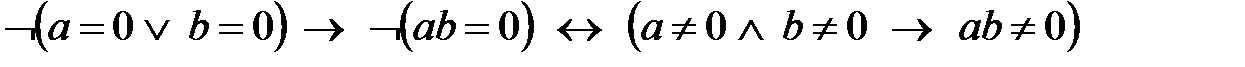 .
.
50. Топ үшін, егер 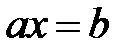 болса, онда
болса, онда 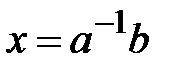 болатынын білеміз. Онда
болатынын білеміз. Онда 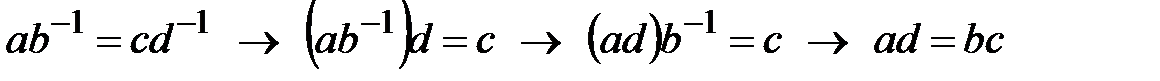 .
.
60. 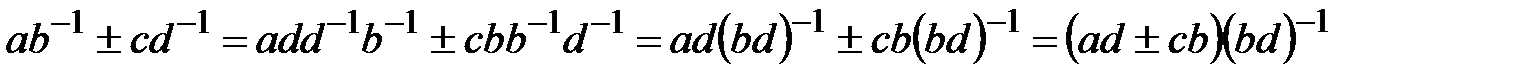 .
.
70 мен 80 топтың қасиетінен шығады. ■
Өріс сақинаның ерекше класс тармағын құрайды.
Анықтама: Өріс – екіден кем емес элементтерден тұратын көпмүшелік, оған екі алгебралық бинарлы амал қолданылады, қосу және көбейту, екеуі де ассоциативті және коммутативті, бір-бірімен дистрибутивті заңмен байланысты, яғни кез-келген 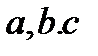 үшін:
үшін:
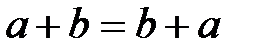
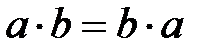

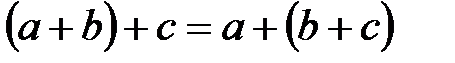
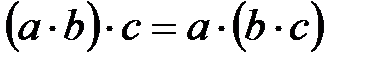
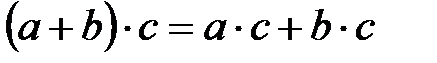
Одан басқа өрісте нөлдік элемент (0) болуы мүмкін, яғни 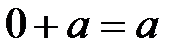 және кез-келген
және кез-келген 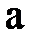 элементі үшін қарама-қарсы
элементі үшін қарама-қарсы 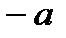 болады, яғни
болады, яғни 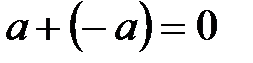 . бірлік элемент үшін
. бірлік элемент үшін 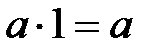
 және кез-келген нөлдік емес элемент
және кез-келген нөлдік емес элемент 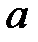 үшін қарсы элемент
үшін қарсы элемент 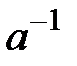 , онда
, онда 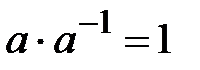 . Өрістің қосу бойынша барлық элементтері өрістің аддиативті тобын, көбейту бойынша өрістің мультипликативті тобын құрайды. Сонымен қатар нөлдік емес өрісте алу және бөлу амалдары да орындалуы мүмкін.
. Өрістің қосу бойынша барлық элементтері өрістің аддиативті тобын, көбейту бойынша өрістің мультипликативті тобын құрайды. Сонымен қатар нөлдік емес өрісте алу және бөлу амалдары да орындалуы мүмкін.
Өрістің қосу және көбейту амалдарының мысалдарына рационал сандар 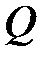 жиыны, нақты сандар
жиыны, нақты сандар 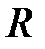 жиыны,
жиыны,  кешен сандар жиыны,
кешен сандар жиыны, 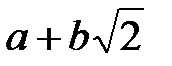 түріндегі барлық сандар жиыны, мұндағы
түріндегі барлық сандар жиыны, мұндағы 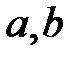 – рационал сандар, барлық алгебралық сандар жиыны, барлық рационалдық функциялар жиыны нақты коэффициентпен бір немесе бірнеше айнымалыдан тұратын. Өрістің элементтерінің жиыны шектеулі де болуы мүмкін. Мұндай өрістер Галуа өрістері деп аталады. Мұндай өрістерге мысал, модулі бойынша сақина өрістерінің айырмасы бола алады.
– рационал сандар, барлық алгебралық сандар жиыны, барлық рационалдық функциялар жиыны нақты коэффициентпен бір немесе бірнеше айнымалыдан тұратын. Өрістің элементтерінің жиыны шектеулі де болуы мүмкін. Мұндай өрістер Галуа өрістері деп аталады. Мұндай өрістерге мысал, модулі бойынша сақина өрістерінің айырмасы бола алады.
Әрбір өріс қарапайым сақина, керсінше де кез-келген нөлдік емес ассоциативті-коммутативті қарапайым сақина бірлігімен өріс бола алады.
Нөлдік емес сандық сақина, сандық өріс деп аталады, егер оның екі 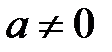 және
және 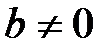 сандарында жеке
сандарында жеке 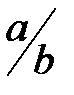 болса.
болса.
Өріс теориясының негізгі мақсаты – берілген өрістің барлық ішөрістерін, кеңейтулерін, өріс классификациясын толығымен изоморфизм және автоморфизм топтарын зерттеу арқылы бейнелеу.
Анықтама: Өріс деп коммутативті сақинаны айтады, мұндағы нөл бірден өзгеше 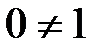 және кез-келген нөлдік емес элемент сақинаның керіленетін элементі болып саналады.
және кез-келген нөлдік емес элемент сақинаның керіленетін элементі болып саналады.
Анықтама: Егер 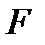 =
= 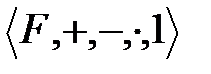 - өріс.
- өріс. 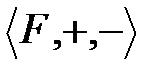 тобы өрістің аддитивті тобы болады, ал оның бейтарап элементі өрістің нөлі деп аталады және 0 белгісімен белгіленеді.
тобы өрістің аддитивті тобы болады, ал оның бейтарап элементі өрістің нөлі деп аталады және 0 белгісімен белгіленеді.
Анықтама: Өрістің 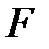 ішөрісі деп
ішөрісі деп 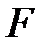 өрістің ішсақинасын атайды, мұндағы әрбір нөлдік емес элемент керіленеді. Өрістің
өрістің ішсақинасын атайды, мұндағы әрбір нөлдік емес элемент керіленеді. Өрістің 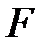 ішөрісі өзіндік ішөріс деп аталады.
ішөрісі өзіндік ішөріс деп аталады.
Өріс қарапайым деп аталады, егер оның өзіндік ішөрістері болмаса.
Кез-келген өрістің жай бір ішөрісі болады.
Теорема 1.1: Егер 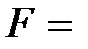
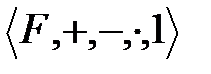 - өріс, онда өрістің кез-келген
- өріс, онда өрістің кез-келген 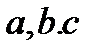 элементтеріне:
элементтеріне:
1. егер 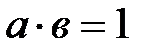 , онда
, онда 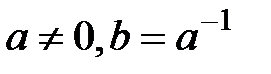

2. егер 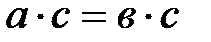 және
және 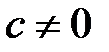 , онда
, онда 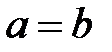
3. егер 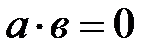 , онда
, онда 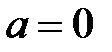 немесе
немесе 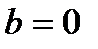
4. егер 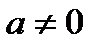 және
және 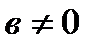 , онда
, онда 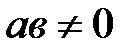
5. 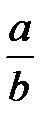 =
= 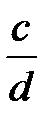 сонда ғана, егер
сонда ғана, егер 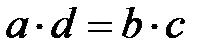 ,
, 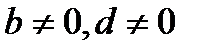
6. 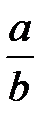
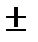
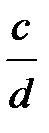 =
= 
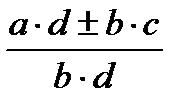
7. 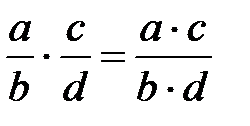
8. 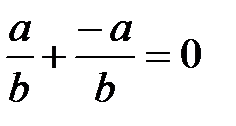 және -
және - 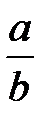 =
= 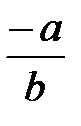
9. егер 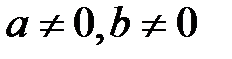 , онда
, онда 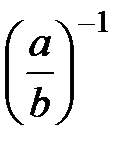 =
= 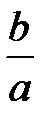
10. 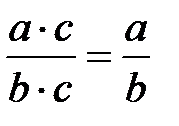
Дәлелдеу:
1. Егер 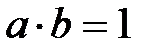 , онда
, онда 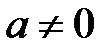 , себебі
, себебі 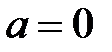 ,
, 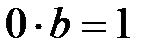
 және
және 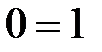 , өрісте мүмкін емес. Ал
, өрісте мүмкін емес. Ал 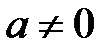 болғанда, оған кері
болғанда, оған кері 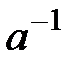 бар.
бар.
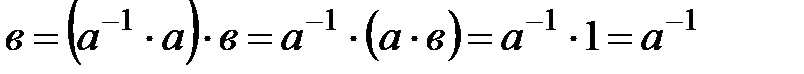
2. Егер 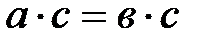 және
және 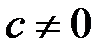 , онда өрісте
, онда өрісте 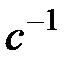 элементі бар және
элементі бар және 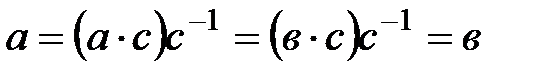 , яғни
, яғни 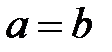 .
.
3. 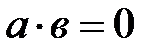 – ден
– ден 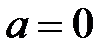 немесе
немесе 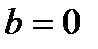 шығады. Егер
шығады. Егер 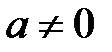 , онда
, онда 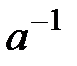 элементі бар және
элементі бар және 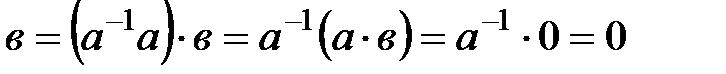

4. (3)-ден контрапозициязаңы бойынша 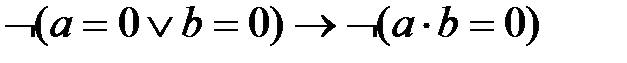 яғни
яғни 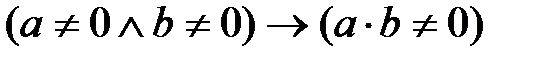
5. Егер 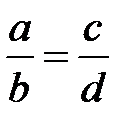 яғни
яғни 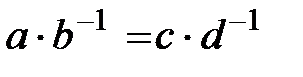
 , онда
, онда 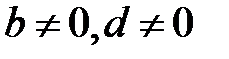 және
және 
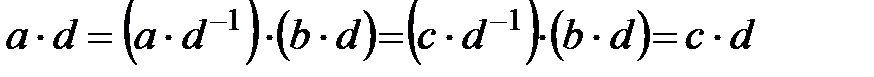 яғни
яғни 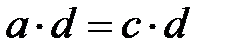 теңсіздігінен
теңсіздігінен 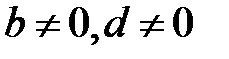 болғанда
болғанда 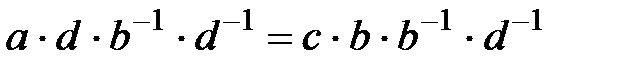 және
және 
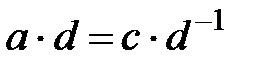
 шығады.
шығады.
6. 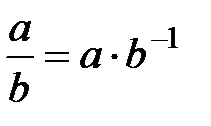 және
және 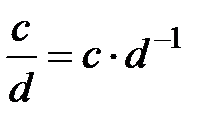 болғандықтан
болғандықтан 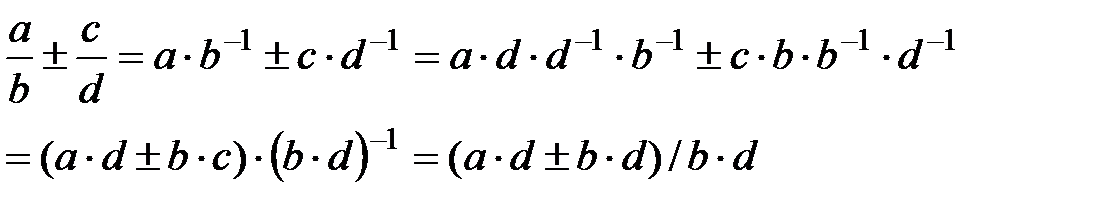
7. 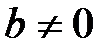 және
және 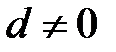 болғанда
болғанда 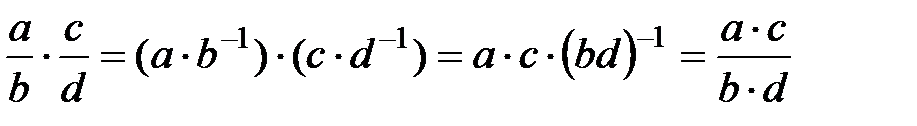
8. 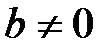 болғанда
болғанда 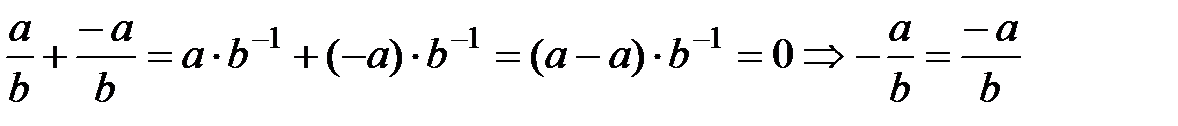
9. Егер 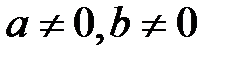 онда
онда 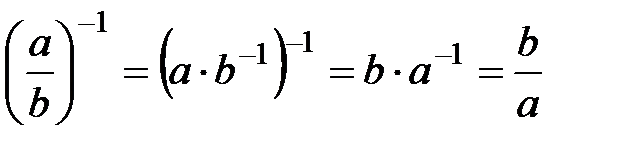
10. 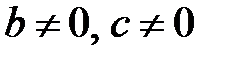 болғанда
болғанда 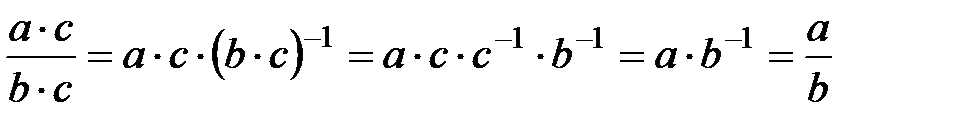
Егер 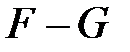 -дің ішөрісі болса, онда
-дің ішөрісі болса, онда 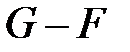 -өрісінің кеңейтілуі деп аталады.
-өрісінің кеңейтілуі деп аталады.
Жай өрістен бастап барлық өрістерді талқылау, бейнелеу үшін кеңейтудің құрылымын зерттеу қажет. 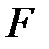 -ке бір элементтің қосылу кеңейтілуі жай деп аталады. Жай кеңейтулердің екі типі бар:
-ке бір элементтің қосылу кеңейтілуі жай деп аталады. Жай кеңейтулердің екі типі бар:
а) Трансцендентті жай кеңейту – ол 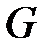 -дің орнына коэффициенттері
-дің орнына коэффициенттері 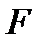 -тен бірайнымалы рационалдық функциялар өрісін алса құрылады.
-тен бірайнымалы рационалдық функциялар өрісін алса құрылады.
в) Алгебралық жай кеңейту – 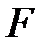 -те жіктелмейтін кейбір
-те жіктелмейтін кейбір 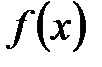 жиынының түбірлерін
жиынының түбірлерін 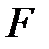 -ке қосқанда және осы түбірде өрнектелетін барлық элементтерден құрылады.
-ке қосқанда және осы түбірде өрнектелетін барлық элементтерден құрылады.
Алгебралық кеңейтудің негізгі класына ақырлы жатады, яғни өрістегі ақырлы өлшемді векторлық кеңістік. Кез-келген кеңейтуді екі әдіспен шығаруға болады: бірінші трансцендентті кеңейту (рационал функциялар өрісін құрып), ал сосын алгебралық. Өрісте алгебралық кеңейту болмайды, егер оның әрбір көпмүшелігі сызықтық жиындарға жіктелетін болса, олар алгебралық тұйық деп аталады. Оған мысал кешен сандар өрісі болады.
Дата добавления: 2016-04-02; просмотров: 3133;
