Рістің алгебралық жай кеңейтілуі
Егер 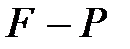 ішөрісі бар өріс болса, онда
ішөрісі бар өріс болса, онда 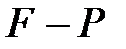 өрісінің кеңейтілуі деп аталады. Қарапайым жағдайда
өрісінің кеңейтілуі деп аталады. Қарапайым жағдайда 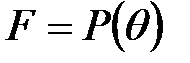 кеңейтілуі
кеңейтілуі 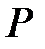 қрісінен және бір ғана
қрісінен және бір ғана 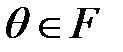 элементінің қосылуымен жасалған.
элементінің қосылуымен жасалған. 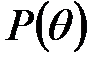
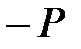 өрісінің жай кеңейтілуі, ал
өрісінің жай кеңейтілуі, ал 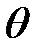 - осы кеңейтудің қарапайым элементі.
- осы кеңейтудің қарапайым элементі.
Егер  бойынша
бойынша 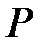 өрісіндегі сақина палиномы болса, мұндағы
өрісіндегі сақина палиномы болса, мұндағы 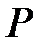 –
– 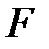 өрісінің ішөрісі.
өрісінің ішөрісі. 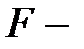 өрісіндегі
өрісіндегі 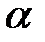 элементі
элементі 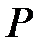 өрісігде алгебралық деп аталады, егер
өрісігде алгебралық деп аталады, егер 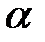
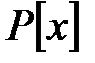 -гі оң дәрежелі кез-келген полиномның түбірі болса.
-гі оң дәрежелі кез-келген полиномның түбірі болса.
Анықтама:  және
және 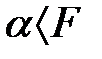 болсын.
болсын. 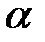 элементі арқылы
элементі арқылы 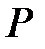 өрісінің жай кеңейтілуі дегеніміз Р жиынынан және
өрісінің жай кеңейтілуі дегеніміз Р жиынынан және 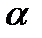 элементінен тұратын
элементінен тұратын 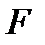 өрісінің ең кіші ішөрісі.
өрісінің ең кіші ішөрісі. 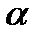 элементі арқылы Р өрісінің жай кеңейтілуі
элементі арқылы Р өрісінің жай кеңейтілуі 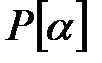 арқылы белгіленеді,
арқылы белгіленеді, 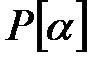 өрісінің негізгі жиыны
өрісінің негізгі жиыны 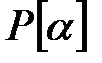 .
.
 ,
, 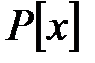
 бойынша – полиномдар сақинасы болсын және
бойынша – полиномдар сақинасы болсын және 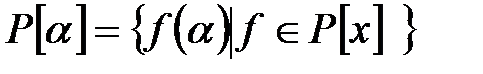 , яғни
, яғни 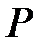
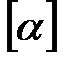
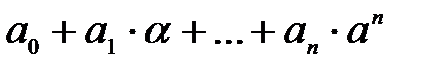 өрнектерінің жиыны, мұндағы
өрнектерінің жиыны, мұндағы 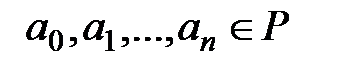 және
және 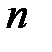 -кез-келген натурал сан.
-кез-келген натурал сан.
Теорема 5.1: 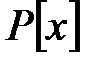
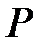 -ғы
-ғы 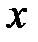 бойынша – полиномдар сақинасы болсын және
бойынша – полиномдар сақинасы болсын және 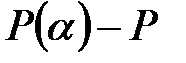 өрісінің жай кеңейтілуі.
өрісінің жай кеңейтілуі.  -тің
-тің 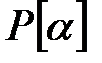 –ға бейнеленуі, сонда
–ға бейнеленуі, сонда 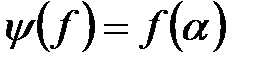
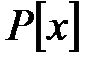 -гі кез-келген
-гі кез-келген 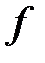 үшін. Сонда:
үшін. Сонда:
а) 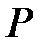 -гі кез-келген
-гі кез-келген 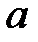 үшін
үшін 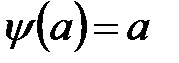
(b) 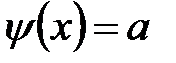
(c) 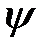 гомоморфизм болып табылады сақина
гомоморфизм болып табылады сақина 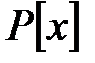 -тен сақина
-тен сақина 
(d) 
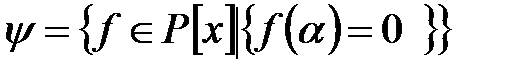 ,
,
(e) 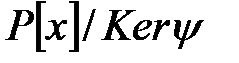 фактор-сақинасы
фактор-сақинасы 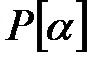 –ға изоморфты.
–ға изоморфты.
Дәлелдеу: 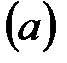 және
және  тұжырымдары
тұжырымдары 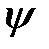 анықтамасынан шығады.
анықтамасынан шығады. 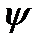 бейнелеуі
бейнелеуі 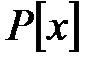 сақинасының негізгі операцияларын сақтайды, себебі
сақинасының негізгі операцияларын сақтайды, себебі 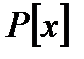 -гі кез-келген
-гі кез-келген 
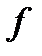 және
және 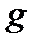 үшін:
үшін:
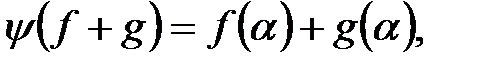
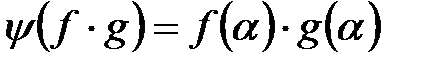 ,
, 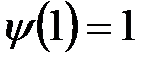
(с) 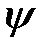 шарты бойынша ол
шарты бойынша ол 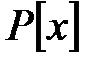 -тің
-тің 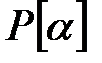 –ға бейнеленуі. Яғни
–ға бейнеленуі. Яғни 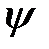 гомоморфизм болып табылады сақина
гомоморфизм болып табылады сақина 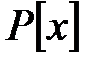 -тен сақина
-тен сақина 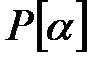
(d) тұжырымы 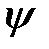 -дің бейнелену анықтамасынан шығады.
-дің бейнелену анықтамасынан шығады.
(е) 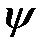 гомоморфизм сақина
гомоморфизм сақина 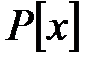 -тен
-тен  –ға болып табылатындықтан, фактор-сақинасы
–ға болып табылатындықтан, фактор-сақинасы 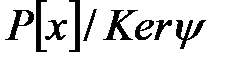 изоморфты
изоморфты 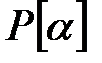 сақинасына.
сақинасына.
Салдар 5.2: 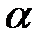 -
- 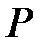 –өрісіндегі трансцендентті элемент,онда
–өрісіндегі трансцендентті элемент,онда 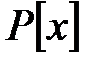 полиномдар сақинасы изоморфты
полиномдар сақинасы изоморфты 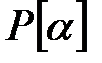 сақинасына.
сақинасына.
Дәлелдеу: 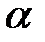 -ның
-ның 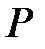
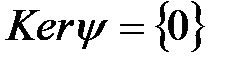 - трансценденттілігіне қатысты. Сондықтан
- трансценденттілігіне қатысты. Сондықтан 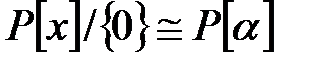 . Сонымен қатар
. Сонымен қатар 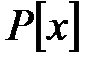 сақинасының фактор-сақинасы нөлдік идеал бойынша
сақинасының фактор-сақинасы нөлдік идеал бойынша 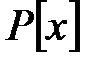 изоморфты. Осыдан
изоморфты. Осыдан 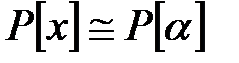
Дата добавления: 2016-04-02; просмотров: 1719;
