Рационал сандар өрісі

Анықтама: өрісі бүтін облыстың дербес өрісі деп аталады, егер келесі шарттар орындалса:

а) Егер 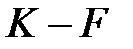өрісінің ішкі сақинасы болса.

в) Кез-келген үшін 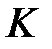сақинасының 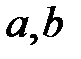элементтері бар және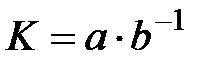

Анықтама:Рационал сандар өрісі деп бүтін сандар сақинасының дербес өрісін айтады. Рационал сандар өрісінің элементтерін рационал сандар деп атайды.

Осы анықтама бойынша кез-келген рационал сан дербес бүтін сан түрінде бола алады.

Рационал сандар өрісіне изоморфты кез-келген өріс, рационал сандар өрісі бола алады.

Анықтама: 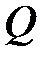рационал сандар жиынының < қатынасы келесі түрде анықталады: кез келген екі рационал сан 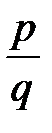және үшін, мұндағы және 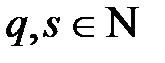, , егер .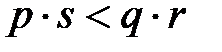

Рационал сандар үшін қосу, алу, көбейту, бөлу амалдары қолданылады, сол себепті олар деп белгіленетін рационал сандар өрісін құрайды. 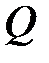өрісі – барлық бүтін сандарды қамтитын, минималь өріс.

Рационал сандар үшін негізгі амалдар:

,

,

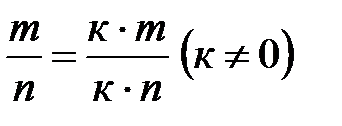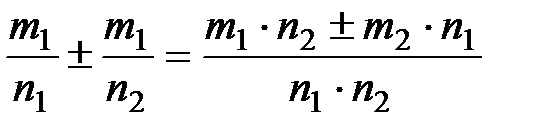
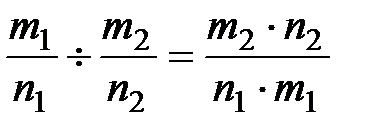
Теорема 2.1: Рационал сандар жиынында бинарлы қатынас < келесі қасиеттер байқалады:

1. 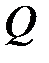-ғы кез-келген үшін, егер және 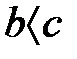, онда .

2. 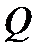-ғы кез-келген 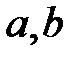үшін, үш қатынастың біреуі ғана орындалады: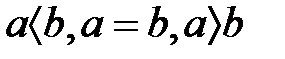

3. -ғы кез-келген үшін, егер , онда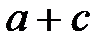

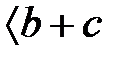
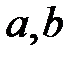4. -ғы кез-келген үшін, егер және , онда

Теорема 2.2: Рационал коэффициенттері бар екінші және үшінші дәрежелі көпмүшелігін рационал сандар өрісіне келтіреміз тек сонда ғана, егер оның кем дегенде бір рационал түбірі бар болса.

Дәлелдеу: 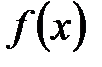– рационал сандар өрісінің 2-ші және 3-ші дәрежелі

көпмүшелігі болсын. Егер 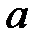көпмүшелігінің рационал түбірі болса,

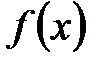
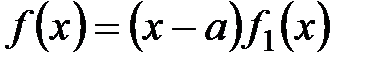онда -ға бөлінеді, яғни , мұндағы 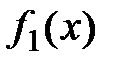- осы рационал сандар өрісінің көпмүшелігі. Мұнда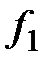 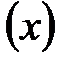көпмүшелігінің дәрежесі 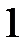немесе тең, осыдан 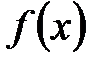көпмүшелігі рационал сандар өрісінде келтіріледі.

Керісінше, егер 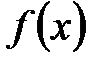көпмүшелігі рационал сандар өрісінде келтірілетін болса, онда көбейткішінің кемдегенде бірі сызықтық болады. 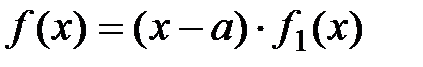, мұндағы 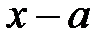және - рационал коэффициенті бар көпмүшеліктер, осындағы 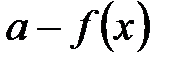-нің рационал түбірі.

Мысалы: көпмүшелікті рационал сандар өрісінде келтірілмейтін көбейткіштерге жіктеу керек.

Рационал түбірді табу жолым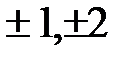ен -ден рационал бір түбірін табамыз, 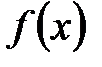-ті 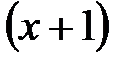-ге бөлеміз. Бұл бөлуді Горнер схемасы арқылы орындауға болады. Екінші дәрежелі көпмүшелігінің рационал түбірі жоқ, сондықтн рационал сандар өрісінде келтірілмейді.

ізделіп отырған көпмүшелігінің жіктелуі.