рістің күрделі алгебралық кеңейтілуі
Өрістің ақырлы кеңейтілуі. Ақырлы өріс немесе Галуа өрісі – элементтер саны ақырлы өріс. 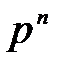 дәрежелі элементтер саны Галуа өрісі. Галуа өрісін алғаш рет 1832 жылы Э. Галуа қарастырды.
дәрежелі элементтер саны Галуа өрісі. Галуа өрісін алғаш рет 1832 жылы Э. Галуа қарастырды.
Кез-келген 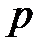 - жай және
- жай және  - натурал саны үшін
- натурал саны үшін 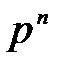 элементтерінің бір ғана өрісі бар. Ол
элементтерінің бір ғана өрісі бар. Ол 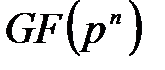 немесе
немесе 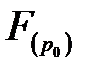 деп белгіленеді. Мұндағы
деп белгіленеді. Мұндағы 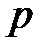 саны -
саны -  өрісінің сипаттамасы, яғни
өрісінің сипаттамасы, яғни 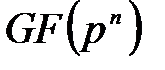 өрісі р-мен сипатталатын жай өріс.
өрісі р-мен сипатталатын жай өріс. 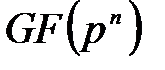 өрісінің
өрісінің 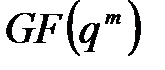 ішөрісі бар болады, сонда ғана, егер p=q және n m-ге бөлінеді.
ішөрісі бар болады, сонда ғана, егер p=q және n m-ге бөлінеді.
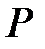 –
– 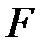 өрісінің ішөрісі болсын. Онда
өрісінің ішөрісі болсын. Онда 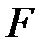 -ті
-ті 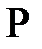 -гі векторлық кеңістік деп қарстыруға болады,
-гі векторлық кеңістік деп қарстыруға болады, 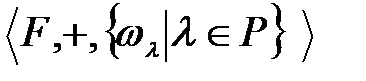 , осындағы
, осындағы 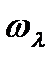 -
- 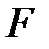 -тің элементтерін
-тің элементтерін 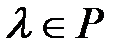 скалярына көбейту амалы.
скалярына көбейту амалы.
Теорема 6.1:  ақырлы өріс үшін және
ақырлы өріс үшін және 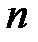 бүтін оң саны үшін, тек қана бір
бүтін оң саны үшін, тек қана бір 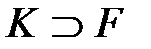 кеңейтілуі бар
кеңейтілуі бар 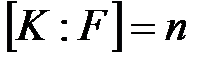 дәрежесінде.
дәрежесінде.
Дәлелдеу: а) Жалғыздық. 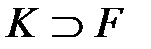 -
- 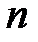 дәрежелі кеңейтілуі болсын.
дәрежелі кеңейтілуі болсын.  және
және 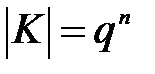 ,
, 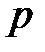 -жай. Осыдан
-жай. Осыдан 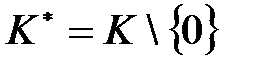 мультипликативті топта
мультипликативті топта  реті бар, ал Логранж теоремасы бойынша реттің әрбір элементі
реті бар, ал Логранж теоремасы бойынша реттің әрбір элементі 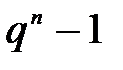 -ді бөледі.
-ді бөледі. 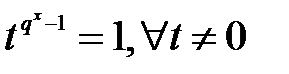 бұл
бұл 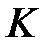 өрісінің барлық элементтері
өрісінің барлық элементтері 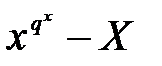 жиынының әртүрлі түбірлері болады
жиынының әртүрлі түбірлері болады 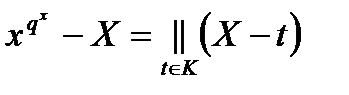 жіктелу орны бар.
жіктелу орны бар. 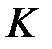 өрісінің ішөрісінің
өрісінің ішөрісінің 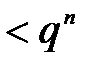 элементтерінің санының мұндай сызықтық жиындарға жіктелуі мүмкін емес, сондықтан
элементтерінің санының мұндай сызықтық жиындарға жіктелуі мүмкін емес, сондықтан 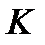 -
- 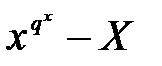 көпмүшелігіне жіктеледі.
көпмүшелігіне жіктеледі.
Анықтама: 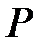 өрісінің
өрісінің  кеңейтілуін ақырлы деп атайды, егер
кеңейтілуін ақырлы деп атайды, егер  - -ғы векторлық кеңістік және ақырлы өлшемділігі болса. Бұл өлшемділік
- -ғы векторлық кеңістік және ақырлы өлшемділігі болса. Бұл өлшемділік 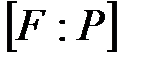 арқылы белгіленеді.
арқылы белгіленеді.
Сөйлем: Егер 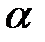 –
– 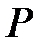 -ғы
-ғы 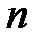 дәрежелі алгебралық элемент болса, онда
дәрежелі алгебралық элемент болса, онда 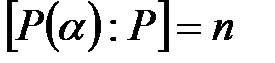
Анықтама: 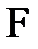 өрісінің
өрісінің 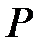 кеңейтілуі алгебралық деп аталады, егер F-гі әрбір элемент Р-да алгебралық болса.
кеңейтілуі алгебралық деп аталады, егер F-гі әрбір элемент Р-да алгебралық болса.
Теорема 6.2:Кез-келген  өрісінің
өрісінің  ақырлы кеңейтілуі
ақырлы кеңейтілуі 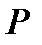 -да алгебралық болады.
-да алгебралық болады.
Дәлелдеу: 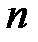 -
- 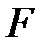 -тің
-тің 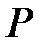 -гі өлшемділігі болсын, теорема дұрыс болады, егер
-гі өлшемділігі болсын, теорема дұрыс болады, егер 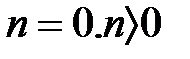 деп жориық, онда
деп жориық, онда 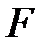 -гі кез-келген
-гі кез-келген 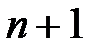 элементі
элементі 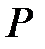 –да сызықтық тәуелді, сонымен қатар
–да сызықтық тәуелді, сонымен қатар  -да нөлге тең емес
-да нөлге тең емес 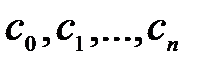 бар, онда
бар, онда 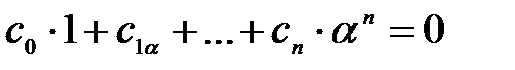 Осыдан
Осыдан 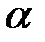 шамасы
шамасы 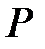 -да алгебралық болады.
-да алгебралық болады.
Сонымен қатар ақырлы емес кеңейтілу болатын алгебралық кеңейтілу бар.
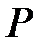 -да
-да 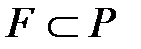 кеңейтілуі алгебралық деп аталады, егер
кеңейтілуі алгебралық деп аталады, егер  -тің барлық элементтері
-тің барлық элементтері  қатысты алгебралық болса.
қатысты алгебралық болса. 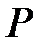 өрісінің
өрісінің  кеңейтілуі күрделі деп аталады, егер өспелі тізбек болса.
кеңейтілуі күрделі деп аталады, егер өспелі тізбек болса.
Теорема 6.3: 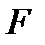 -
- 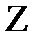 өрісінің ақырлы кеңейтілуі, ал
өрісінің ақырлы кеңейтілуі, ал  -
- 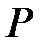 өрісінің ақырлы кеңейтілуі болса, онда
өрісінің ақырлы кеңейтілуі болса, онда 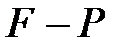 өрісінің ақырлы кеңейтілуі болады және
өрісінің ақырлы кеңейтілуі болады және  .
.
Дәлелдеу: (1). 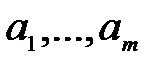 -
- 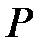 -ғы
-ғы 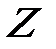 өрісінің базисі және
өрісінің базисі және
(2) 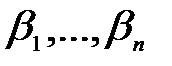 -
-  -гі
-гі 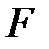 өрісінің базисі.
өрісінің базисі. 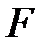 -гі кез-келген
-гі кез-келген  элементін базис арқылы келесі түрде сызықты бейнелеуге болады:
элементін базис арқылы келесі түрде сызықты бейнелеуге болады:
(3) 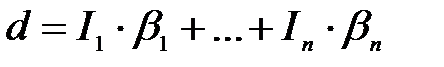
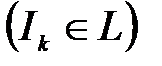 .
.
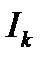 коэффициенттерін (1) базис арқылы сызықты бейнелеуге болады:
коэффициенттерін (1) базис арқылы сызықты бейнелеуге болады:
(4) 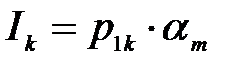
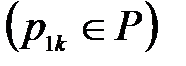 .
.
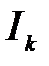 коэффициенттері үшін (3) –ге мән бере отырып, аламыз:
коэффициенттері үшін (3) –ге мән бере отырып, аламыз: 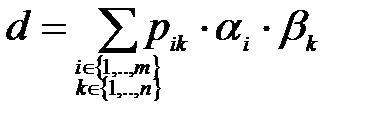
Сонымен 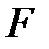 өрісінің әрбір элементін
өрісінің әрбір элементін  жиынының сызықтық комбинациясы түрінде белгілейік:
жиынының сызықтық комбинациясы түрінде белгілейік: 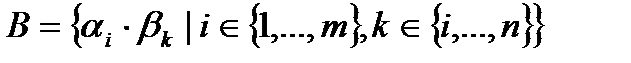 .
.
В жиыны 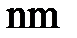 элементтерінен тұрады.
элементтерінен тұрады.
 өрісіндегі
өрісіндегі 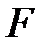 -тің базисі. Бізге
-тің базисі. Бізге 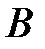 элементтер жүйесінің жиыны сызықты тәуелсіз екенін көрсету қажет. Онда:
элементтер жүйесінің жиыны сызықты тәуелсіз екенін көрсету қажет. Онда:
(5) 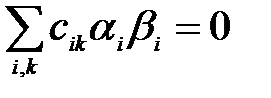 мұндағы
мұндағы 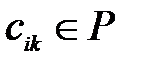 . Себебі
. Себебі  -гі (2) жүйе сызықты тәуелсіз, онда (5) –ші теңдіктен шығады
-гі (2) жүйе сызықты тәуелсіз, онда (5) –ші теңдіктен шығады
(6) 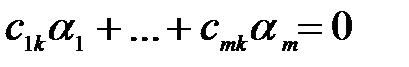
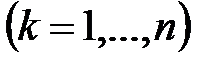 Себебі
Себебі 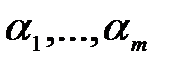 элементтері
элементтері 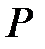 -да сызықтық тәуелсіз, онда (6) теңсіздіктен шығады:
-да сызықтық тәуелсіз, онда (6) теңсіздіктен шығады:
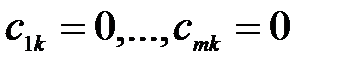
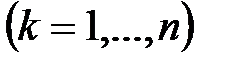 бұл (5)-тің барлық коэффициенттері нөлге тең екенін көрсетеді. Сондықтан
бұл (5)-тің барлық коэффициенттері нөлге тең екенін көрсетеді. Сондықтан 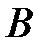 элементтер жүйесі сызықтық тәуелсіз және
элементтер жүйесі сызықтық тәуелсіз және 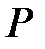 -ғы
-ғы 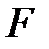 -тің базисі болады.
-тің базисі болады.
Осыдан  , яғни
, яғни 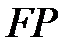 өрісінің ақырлы кеңейтілуі.
өрісінің ақырлы кеңейтілуі.
Анықтама: 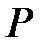 өрісінің
өрісінің 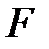 кеңейтілуі алгебралық құрама деп аталады, егер
кеңейтілуі алгебралық құрама деп аталады, егер  өрісінің ішөрістерінің өспелі тізбегі болса.
өрісінің ішөрістерінің өспелі тізбегі болса.
(1) 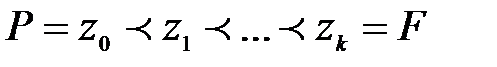
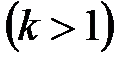 ,мұнда
,мұнда  өрісі
өрісі 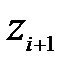 өрісінің жай
өрісінің жай
алгебралық кеңейтілуі. 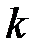 cаны тізбектің ұзындығы деп аталады.
cаны тізбектің ұзындығы деп аталады.
Салдар 6.4: 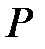 өрісінің
өрісінің  алгебралық құрама кеңейтілуі
алгебралық құрама кеңейтілуі 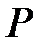 өрісінің ақырлы кеңейтілуі болып табылады.
өрісінің ақырлы кеңейтілуі болып табылады.
Бұл салдардар (1) тізбектің ұзындығының индукциясымен дәлелденеді.
Теорема 6.5: 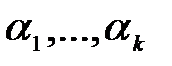
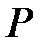 өрісінде алгебралық
өрісінде алгебралық 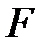 өрісінің элементтері. Онда
өрісінің элементтері. Онда 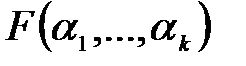
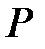 өрісінің ақырлы кеңейтілімі болады.
өрісінің ақырлы кеңейтілімі болады.
Дәлелдеу: 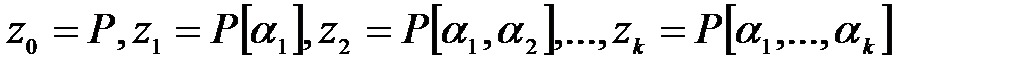
Онда 
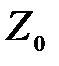
 өрісінің жай алгебралық кеңейтілуі;
өрісінің жай алгебралық кеңейтілуі; 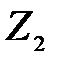 -
-  өрісінің алгебралық жай кеңейтілуі, себебі
өрісінің алгебралық жай кеңейтілуі, себебі
 .
.
Сондықтан 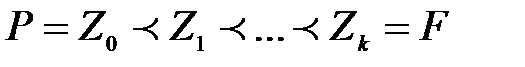 мұндағы
мұндағы 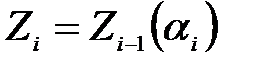
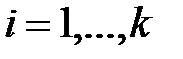 , яғни (2) тізбектің барлық мүшелері алдыңғы тізбектің мүшесінің жай алгебралық кеңейтілуі. Осыдан
, яғни (2) тізбектің барлық мүшелері алдыңғы тізбектің мүшесінің жай алгебралық кеңейтілуі. Осыдан 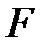 өрісі
өрісі 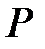 өрісінің алгебралық құрамды кеңейтілуі. Яғни
өрісінің алгебралық құрамды кеңейтілуі. Яғни 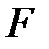 өрісі
өрісі 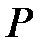 өрісінің ақырлы кеңейтілуі болады.
өрісінің ақырлы кеңейтілуі болады.
Салдар 6.6: Өрістің құрамды алгебралық кеңейтілуі осы өрістің алгебралық кеңейтілуі.
Теорема 6.7: 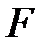 сандық өрісі
сандық өрісі  өрісінің құрама алгебралық кеңейтілуі болсын. Онда
өрісінің құрама алгебралық кеңейтілуі болсын. Онда 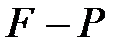 өрісінің жай алгебралық кеңейтілуі болады
өрісінің жай алгебралық кеңейтілуі болады
Дәлелдеу: 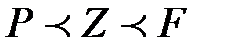 болсын, мұнда
болсын, мұнда 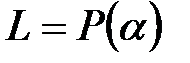 ,
, 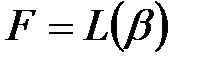 осыдан
осыдан 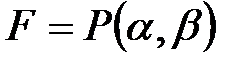
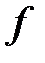 және
және 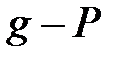 -гі
-гі 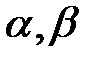 сандарына сәйкес минималды полиномдар болсын және
сандарына сәйкес минималды полиномдар болсын және  .
. 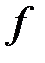 және
және 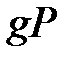 -да келтірілмейді және
-да келтірілмейді және  кешен сандар өрісінде еселі түбірі жоқ.
кешен сандар өрісінде еселі түбірі жоқ.
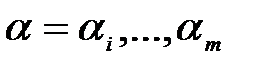 -
-  -гі
-гі 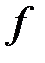 полиномының түбірлері.
полиномының түбірлері.
 -
-  -гі
-гі 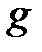 полиномының түбірлері.
полиномының түбірлері.
Ақырлы 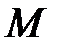 жиынын қарастырайық:
жиынын қарастырайық:
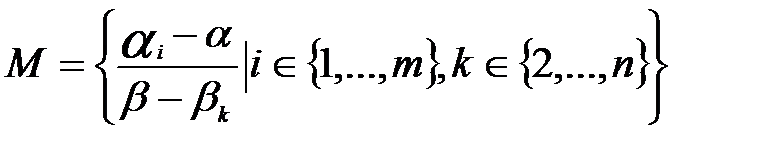
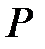 – сандық жиын болғандықтан,
– сандық жиын болғандықтан, 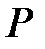 -да
-да  саны бар
саны бар  жиынының элементттерінен өзгеше,
жиынының элементттерінен өзгеше, 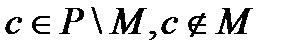
(1) 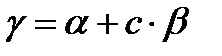 онда келесі қатынастар орындалады:
онда келесі қатынастар орындалады:
(2) 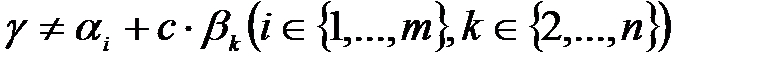 шынында да
шынында да 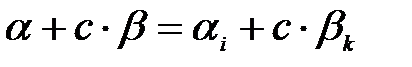 теңдігі жағдайында
теңдігі жағдайында 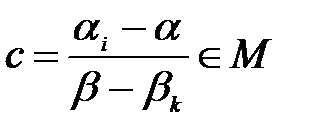 боушы еді, бірақ бұл
боушы еді, бірақ бұл  санын таңдауға қайшы келеді.
санын таңдауға қайшы келеді.
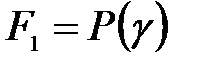 және
және 
 бойынша полиномдар сақинасы.
бойынша полиномдар сақинасы. 
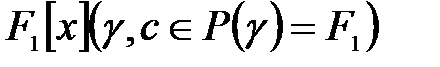 -гі полином.
-гі полином. 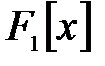 сақинасында
сақинасында 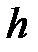 және
және 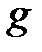 полиномдарының ең үлкен бөлгіші
полиномдарының ең үлкен бөлгіші 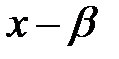 екенін көрейік.
екенін көрейік. 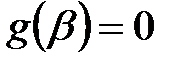 болғандықтан, ол
болғандықтан, ол 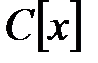 -де
-де 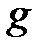 -ді
-ді 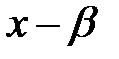 бөледі. (1) қатысты
бөледі. (1) қатысты 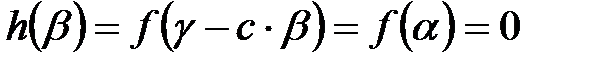 Сондықтан
Сондықтан 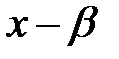 полиномы
полиномы 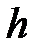 -да
-да 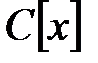 -де бөледі. Осыдан
-де бөледі. Осыдан 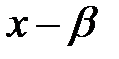
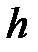 пен
пен 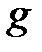 –дің ортақ бөлгіші.
–дің ортақ бөлгіші.
 және
және 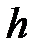
 -де
-де  -дан өзгеше түбірлері жоқ екенін дәлелдейік.
-дан өзгеше түбірлері жоқ екенін дәлелдейік. 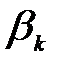 ,
, 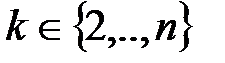 олардың ортақ түбірі деп ұйғарайық. Онда
олардың ортақ түбірі деп ұйғарайық. Онда 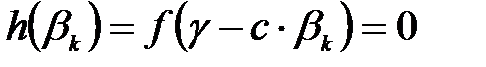 . Осыдан
. Осыдан 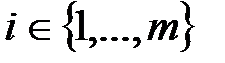 индексі табылады,
индексі табылады, 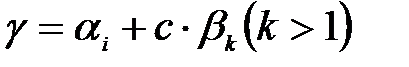 , бұл (2) қарама-қарсы. Осының негізінде
, бұл (2) қарама-қарсы. Осының негізінде 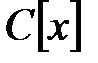 -де
-де  пен
пен 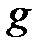 –дің ортақ бөлгіші
–дің ортақ бөлгіші 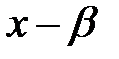 болады.
болады.  - нормаланған полином , осыдан
- нормаланған полином , осыдан 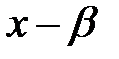
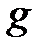 және
және 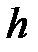 –тің
–тің 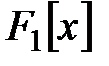 сақинасында ең үлкен ортақ бөлгіш. Сондықтан
сақинасында ең үлкен ортақ бөлгіш. Сондықтан 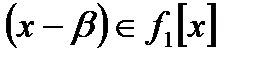 және
және 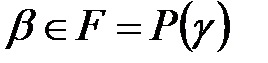 одан басқа
одан басқа 
Олай болса  . Яғни
. Яғни 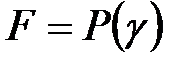 .
. 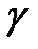 -
-  - ның алгебралық элементі, онда
- ның алгебралық элементі, онда 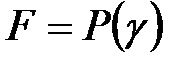 өрісі ізделініп отырған
өрісі ізделініп отырған 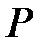 өрісінің алгебралық жай кеңейтілуі.
өрісінің алгебралық жай кеңейтілуі.
Алгебралық сандар өрісі.
Анықтама:  саны алгебралық деп аталады кейбір
саны алгебралық деп аталады кейбір 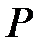 сандық өрісіне қатысты, егер ол кез-келген бір теңдеудің түбірі болса, барлық коэффициенттері
сандық өрісіне қатысты, егер ол кез-келген бір теңдеудің түбірі болса, барлық коэффициенттері 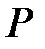 -ға тиісті болса:
-ға тиісті болса: 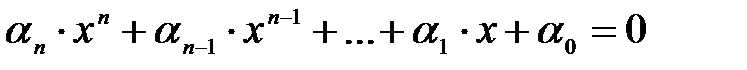 , яғни келесі теңдік орындалады:
, яғни келесі теңдік орындалады: 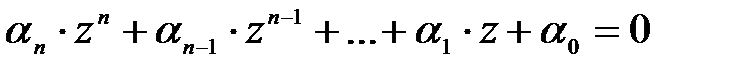
 қатысты алгебралық емес сан,
қатысты алгебралық емес сан,  қатысты трансцендентті деп аталады.
қатысты трансцендентті деп аталады.
Теорема 6.8: Барлық алгебралық сандардың 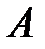 жиыны кешен сандар ¢=
жиыны кешен сандар ¢= 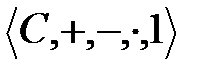
 сақинасында тұйық.
сақинасында тұйық. 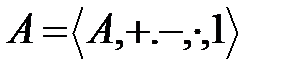 алгебрасы ¢ өрісінің өрісі және ішөрісі болады.
алгебрасы ¢ өрісінің өрісі және ішөрісі болады.
Дәлелдеу: 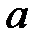 және
және 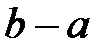 -ның кез-келген элементтері, 6.6 салдары бойынша
-ның кез-келген элементтері, 6.6 салдары бойынша 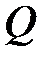 -де
-де 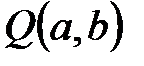 өрісі алгебралық. Сондықтан
өрісі алгебралық. Сондықтан 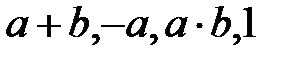 сандары алгебралық, яғни
сандары алгебралық, яғни  жиынына тиісті. Олай болса,
жиынына тиісті. Олай болса, 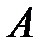 жиыны
жиыны  сақинасының басты амалдарына қатысты тұйық. Сондықтан
сақинасының басты амалдарына қатысты тұйық. Сондықтан 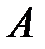 алгебрасы
алгебрасы 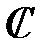 сақинасының ішсақинасы – сақина болады.
сақинасының ішсақинасы – сақина болады.
Егер 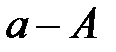 -ғы нөлдік емес элементболса, онда
-ғы нөлдік емес элементболса, онда 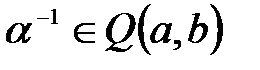 және сондықтан
және сондықтан 
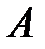 -на тиісті. Осыдан
-на тиісті. Осыдан  алгебрасы
алгебрасы 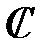 өрісінің ішөрісі және өрісі болады.
өрісінің ішөрісі және өрісі болады.
Анықтама:  өрісі алгебралық сандар өрісі деп аталады.
өрісі алгебралық сандар өрісі деп аталады.
Дата добавления: 2016-04-02; просмотров: 2883;
